Промежутки знакопостоянства

		0		3
	–	0	+	0	+

II. Исследование графика функции по первой производной.

Для нахождения участков монотонности и экстремальных точек найдем первую производную функции:

.

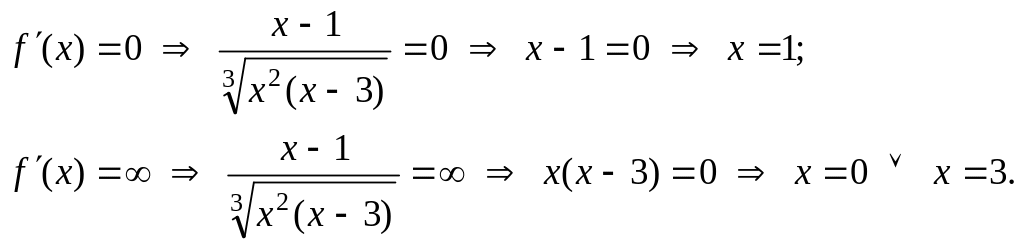
к. т. I.

Область определения функции разобьем на интервалы и определим знак в каждом из них (для удобства вычислений в каждом интервале выбираем фиксированную точку). Результаты исследования знака производной на интервалах между критическими точками (с учетом ) с указанием поведения функции на этих интервалах занесем в таблицу:

		0		1		3
	+		+	0	–		+
		0

Так как функция в точке определена и непрерывна и при переходе через нее меняет знак с плюса на минус, то в этой точке максимум, причем . В точке функция определена и непрерывна и при переходе через нее меняет знак с минуса на плюс, следовательно, в этой точке минимум, причем .

III. Исследование графика функции по второй производной.

Для нахождения участков выпуклости вверх и вниз найдем вторую производную функции

.

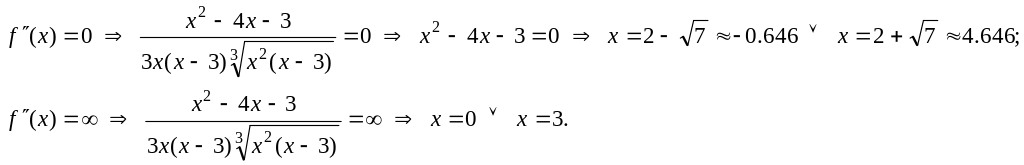
к. т. II.

Область определения функции разобьем на интервалы , и определим знак в каждом из них. Результат исследования знака функции на указанных интервалах с указанием выпуклости вверх и вниз запишем в таблицу:

		–0.646		0		3		4.646
	–	0	+		–		–	0	+
				0		0

При переходе через точки вторая производная меняет знак, следовательно, это точки перегиба функции, причем

,

.

Точки перегиба: .

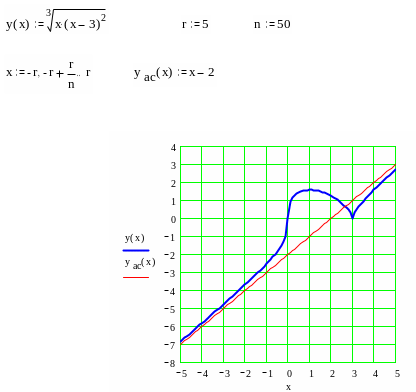
Построение графика начнем с нанесения асимптот, точек пересечения с осями координат, экстремума, перегиба и фрагментов графика функции вблизи этих точек и асимптот.

В окончательном виде график изображен на следующем рисунке.

▼

Пример 15. Провести полное исследование функции и построить ее график.

▲ Исследование функции будем проводить, придерживаясь приведенной выше схемы.

I. Элементарное исследование

• Область определения функции. .

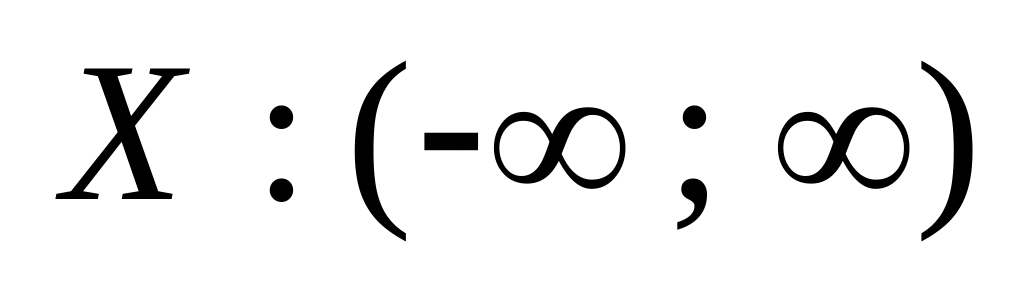• Исследуем функцию на симметричность (определить четность и нечетность функции) и периодичность.

Функция общего вида.

. Функция не периодична.

• Выясним существование асимптот.

Вертикальных асимптот нет, так как нет точек разрыва.

Найдем наклонные асимптоты .

Слева .

. Слева наклонной асимптоты нет.

Справа .

,

.

Справа горизонтальная асимптота: .

• Определим точки пересечения графика функции с координатными осями, найдем интервалы знакопостоянства функции.

Точки пересечения с осью : .

Точки пересечения с осью : .

Промежутки знакопостоянства

		0
	–	0	+

II. Исследование графика функции по первой производной.

Для нахождения участков монотонности и экстремальных точек найдем первую производную функции:

.

к. т. I.

Область определения функции разобьем на интервалы и определим знак в каждом из них (для удобства вычислений в каждом интервале выбираем фиксированную точку). Результаты исследования знака производной на интервалах между критическими точками (с учетом ) с указанием поведения функции на этих интервалах занесем в таблицу:

		1
	+	0	–

Так как функция в точке определена и непрерывна и при переходе через нее меняет знак с плюса на минус, то в этой точке максимум, причем .

III. Исследование графика функции по второй производной.

Для нахождения участков выпуклости вверх и вниз найдем вторую производную функции

.

к. т. II.

Область определения функции разобьем на интервалы и определим знак в каждом из них. Результат исследования знака функции на указанных интервалах с указанием выпуклости вверх и вниз запишем в таблицу:

		2
	–	0	+

При переходе через точку вторая производная меняет знак, следовательно, это точка перегиба функции, причем . Точка перегиба: .

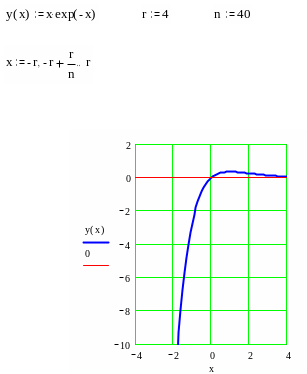
Построение графика начнем с нанесения асимптот, точек пересечения с осями координат, экстремума, перегиба и фрагментов графика функции вблизи этих точек и асимптот.

В окончательном виде график изображен на следующем рисунке.

▼

Пример 16. Провести полное исследование функции и построить ее график.

▲ Исследование функции будем проводить, придерживаясь приведенной выше схемы.

I. Элементарное исследование

• Область определения функции . Точка разрыва: .

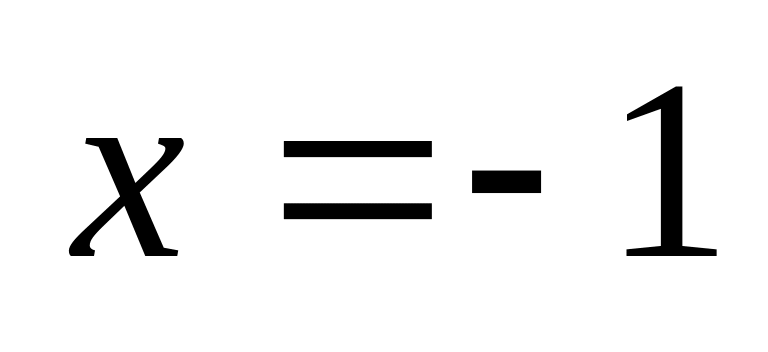• Исследуем функцию на симметричность (определить четность и нечетность функции) и периодичность.

Функция общего вида.

. Функция не периодична.

• Выясним существование асимптот. В точке функция имеет разрыв II рода, ибо,

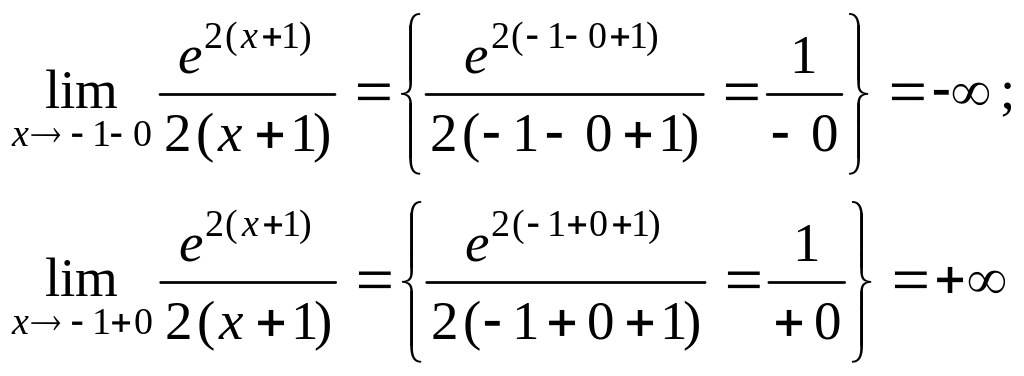
в остальных точках она непрерывна. Прямая является вертикальной асимптотой.

Найдем наклонные асимптоты .

Слева .

,

.

Уравнение горизонтальной асимптоты слева: .

Справа .

.

Справа наклонной асимптоты нет.

• Определим точки пересечения графика функции с координатными осями, найдем интервалы знакопостоянства функции.

Точки пересечения с осью : Точек пересечения с осью нет.

Точки пересечения с осью : Точка пересечения с осью : .

Промежутки знакопостоянства

		–1
	–		+

II. Исследование графика функции по первой производной.

Для нахождения участков монотонности и экстремальных точек найдем первую производную функции:

.

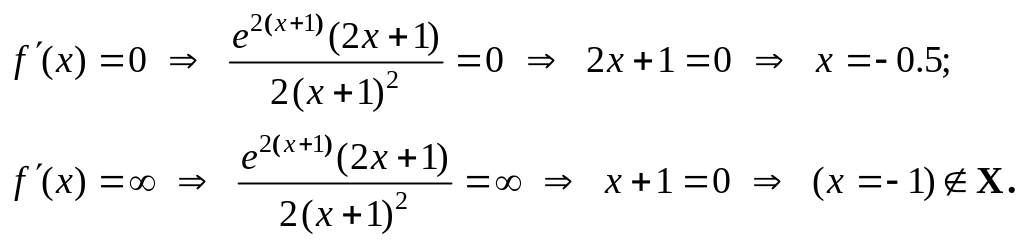
к. т. I.

Область определения функции разобьем на интервалы и определим знак в каждом из них (для удобства вычислений в каждом интервале выбираем фиксированную точку). Результаты исследования знака производной на интервалах между критическими точками (с учетом ) с указанием поведения функции на этих интервалах занесем в таблицу:

		–1		–0.5
	–		–	0	+

Так как функция в точке определена и непрерывна и при переходе через нее меняет знак с минуса на плюс, то в этой точке минимум, причем .

III. Исследование графика функции по второй производной.

Для нахождения участков выпуклости вверх и вниз найдем вторую производную функции

.

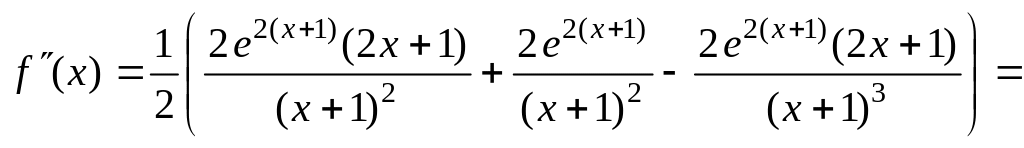
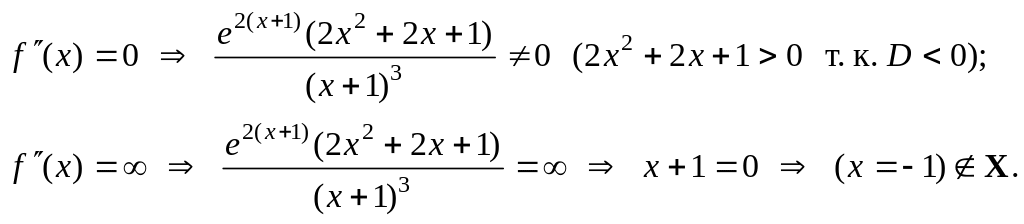к. т. II нет.

Область определения функции разобьем на интервалы и определим знак в каждом из них. Результат исследования знака функции на указанных интервалах с указанием выпуклости вверх и вниз запишем в таблицу:

		–1
	–		+

Точек перегиба нет.

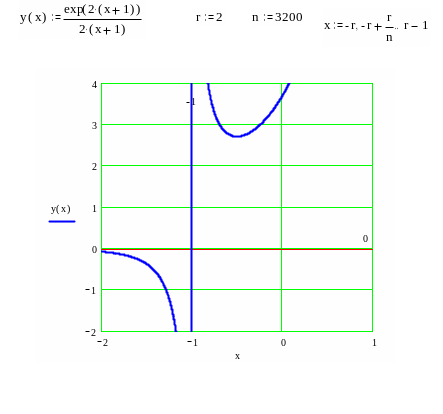
Построение графика начнем с нанесения асимптот, точек пересечения с осями координат, экстремума, перегиба и фрагментов графика функции вблизи этих точек и асимптот.

В окончательном виде график изображен на следующем рисунке.

Пример 17. Провести полное исследование функции и построить ее график.

▲ Исследование функции будем проводить, придерживаясь приведенной выше схемы.

I. Элементарное исследование

• Область определения функции. .

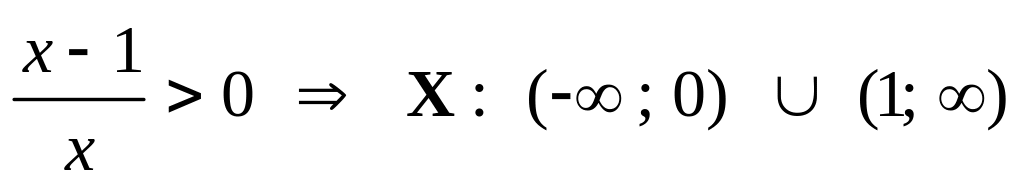• Исследуем функцию на симметричность (определить четность и нечетность функции) и периодичность.

Функция общего вида.

. Функция не периодична.

• Выясним существование асимптот. Вертикальная асимптота может существовать лишь на конечных границах области определения. Найдем

.

Значит, прямая – вертикальная асимптота.

Найдем

.

Следовательно, прямая – вертикальная асимптота.

Найдем наклонные асимптоты .

Слева .

,

.

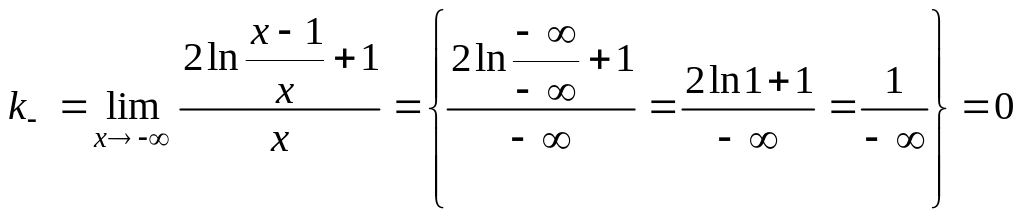Уравнение горизонтальной асимптоты слева .

Справа .

,

.

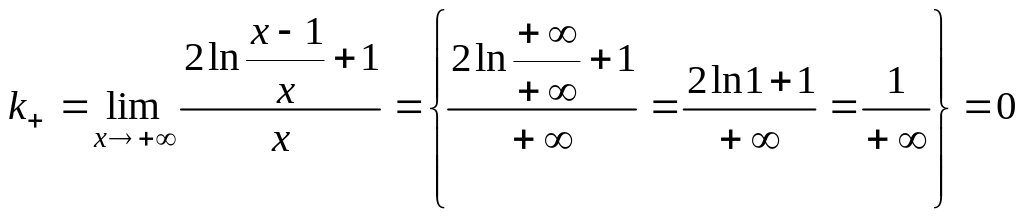Уравнение горизонтальной асимптоты справа .

• Определим точки пересечения графика функции с координатными осями, найдем интервалы знакопостоянства функции.

Точки пересечения с осью :

Точка пересечения с осью : .

Точек пересечения с осью нет.

Промежутки знакопостоянства

		0	1		2.533
	+			–	0	+

II. Исследование графика функции по первой производной.

Для нахождения участков монотонности и экстремальных точек найдем первую производную функции:

.

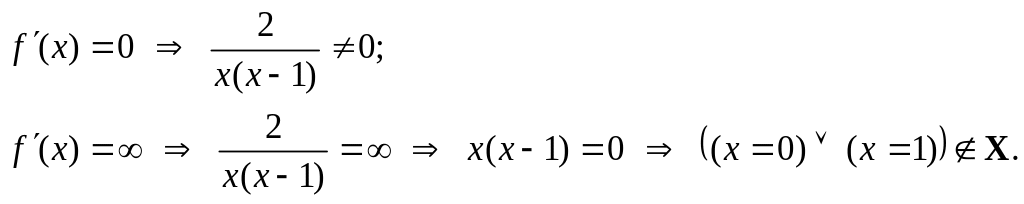к. т. I нет.

Область определения функции разобьем на интервалы и определим знак в каждом из них (для удобства вычислений в каждом интервале выбираем фиксированную точку). Результаты исследования знака производной на интервалах между критическими точками (с учетом ) с указанием поведения функции на этих интервалах занесем в таблицу:

		0	1
	+			+

Экстремумов нет.

III. Исследование графика функции по второй производной.

Для нахождения участков выпуклости вверх и вниз найдем вторую производную функции

.

;

.

К. т. II нет.

Область определения функции разобьем на интервалы и определим знак в каждом из них. Результат исследования знака функции на указанных интервалах с указанием выпуклости вверх и вниз запишем в таблицу:

		0	1
	+			–

Точек перегиба нет.

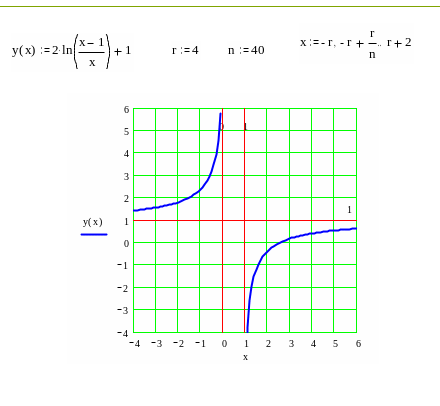
Построение графика начнем с нанесения асимптот, точек пересечения с осями координат, экстремума, перегиба и фрагментов графика функции вблизи этих точек и асимптот.

В окончательном виде график изображен на следующем рисунке.

▼