2. Интервалы выпуклости и вогнутости графика функции, точки перегиба

Пусть дана кривая уравнением и пусть функция в точке имеет конечную производную , т. е. в точке существует касательная к данной кривой, не параллельная оси .

Определение. Если существует такая окрестность точки , что все точки данной кривой, абсциссы которых содержатся в этой окрестности, расположены над касательной к кривой в точке , то говорят, что данная кривая выпукла вниз в точке .

Если все точки кривой с абсциссами из некоторой окрестности точки находятся под касательной к этой кривой в точке , то говорят, что данная кривая выпукла вверх в данной точке .

З амечание. Часто дуги кривой, обращенные выпуклостью вверх, называют выпуклыми, а дуги кривой, обращенные выпуклостью вниз, – вогнутыми.

y y

O a b x O a b x

Достаточным условием выпуклости функции вверх (вниз) на интервале является отрицательность (положительность) ее второй производной в каждой точке интервала, т. е.

если , то функция выпукла вверх на интервале ,

а если , то она на нем выпукла вниз.

_

+

При построении графиков функций бывает полезно выделять точки перегиба графика.

Определение. Точка графика функции называется точкой перегиба кривой , если существует окрестность точки такая, что на множестве выпуклость кривой направлена в одну сторону, а на множестве – в противоположную сторону.

y

M₀

O x₀ x

Теорема 3.1 (необходимое условие точек перегиба). Для того чтобы точка была точкой перегиба функции , определенной и дифференцируемой в окрестности этой точки, необходимо выполнение одного из двух условий: 1) либо , 2) либо не существует.

Внутренние точки области определения функции, в которых вторая производная функции равна нулю или не существует, называются критическими точками второго рода (к. т. II).

Теорема 3.2 (достаточное условие точек перегиба). Пусть функция имеет вторую производную в некоторой окрестности точки , непрерывную в точке . Если и при переходе через точку вторая производная меняет знак, то точка есть точка перегиба кривой .

Замечание. Если всюду на интервале , то – линейная функция, и направление выпуклости прямой можно считать произвольным.

Практическое правило нахождения точек перегиба и участков выпуклости и вогнутости функции

1. Сначала находятся критические точки второго рода, т.е. точки, в которых вторая производная равна нулю или не существует.

2. Затем область определения функции разбивается на интервалы критическими точками и точками разрыва функции и определяется знак второй производной в каждом из полученных интервалов (для чего достаточно определить знак в какой-либо одной точке каждого интервала). Если при переходе через эти точки вторая производная меняет знак, то эти точки являются точками перегиба функции, если смены знака второй производной не происходит, то точки не являются точками перегиба. При этом на тех интервалах, где , функция выпукла вниз, где , – выпукла вверх.

Порядок действий при этом рекомендуется следующий.

1. Найти область определения функции.

2. Найти .

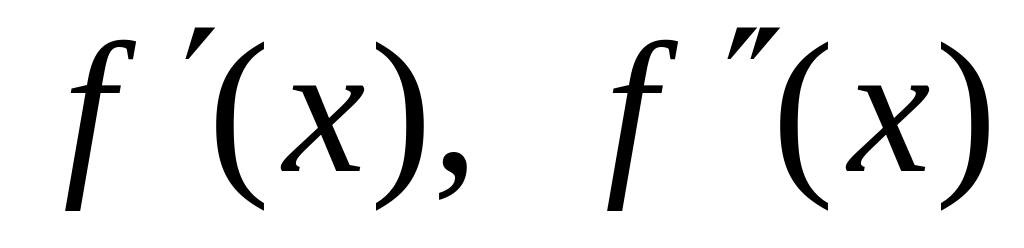3. Определить критические точки второго рода и пронумеровать их в порядке возрастания.

4. Составить таблицу II.

	Интервалы выпуклости, вогнутости и к. т. II
	на интервалах и поведение в к. т. II
	Поведение графика функции на интервалах выпуклости, вогнутости и значение функции в к. т. II

Пример 6. Найти интервалы выпуклости, вогнутости и точки перегиба функции .

1. ▲ Областью существования функции является весь бесконечный интервал .

2. Найдем производные: .

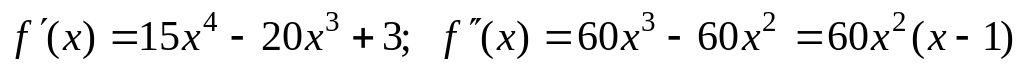3. Вторая производная существует при всех и равна нулю 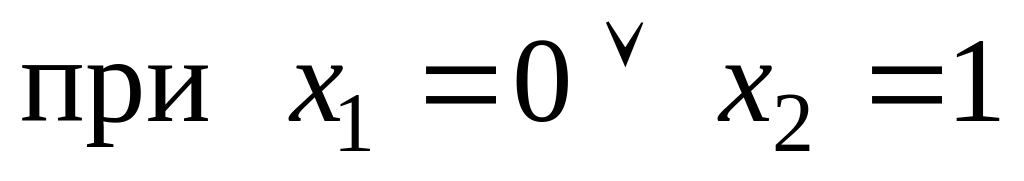. Критическая точка II рода 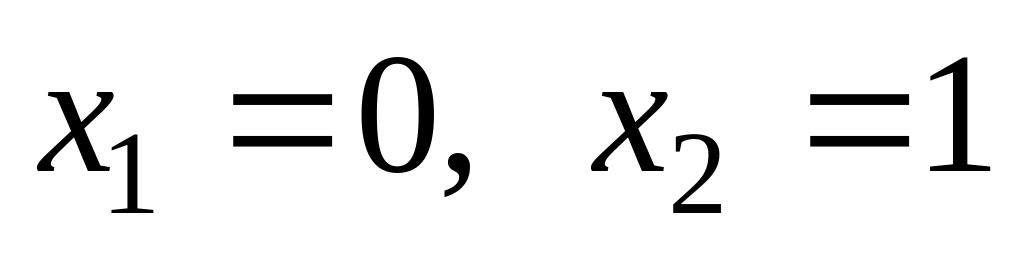. Разобьем область определения функции на интервалы 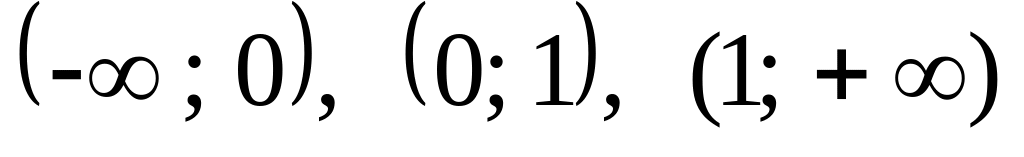и определим знак 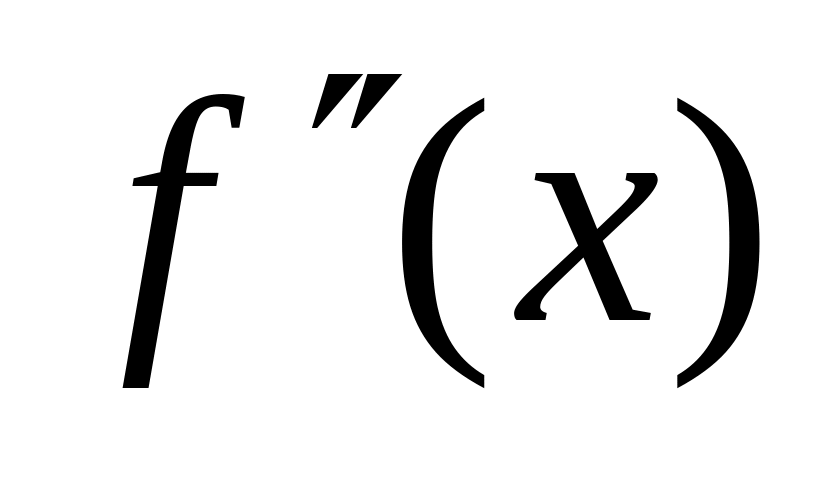в каждом из них. Для этого достаточно определить знак в какой-либо одной точке интервала. Удобно взять точки .

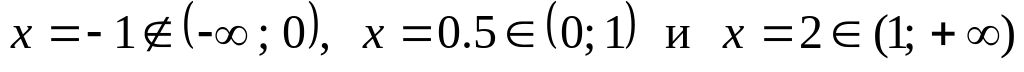Так как , то на интервале функция выпукла вверх;

так как , то на интервале функция выпукла вверх;

так как , то на интервале функция выпукла вниз.

Вторая производная равна нулю . При переходе через точку вторая производная не меняет знак, следовательно, в точке функция перегиба не имеет. При переходе через точку вторая производная меняет знак, следовательно, в точке функция имеет перегиб.

4. Составим таблицу II.

		0		1		▼
	–	0	–	0	+
		Нет т. п.

Замечание. Условимся в дальнейшем выпуклость вверх и выпуклость вниз графика в таблице обозначать так: .

Пример 7. Найти интервалы выпуклости, вогнутости и точки перегиба функции .

1. ▲ Область определения функции .

2. Найдем производные: ,

.

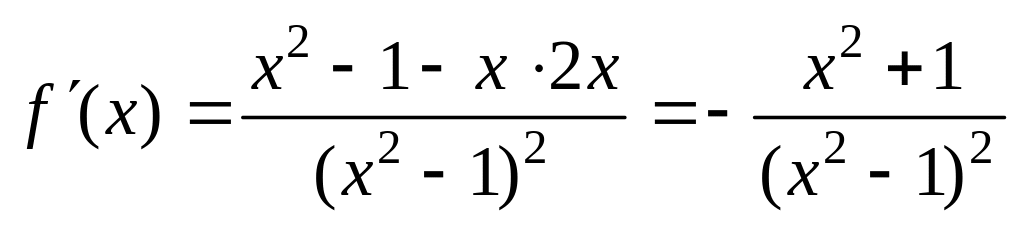3. Вторая производная не существует и равна нулю. Вторая производная равна нулю . Единственная критическая точка второго рода , так как точки 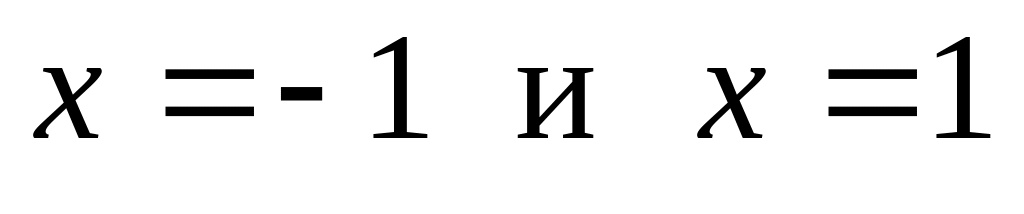области определения не принадлежат. Разобьем область определения функции на интервалы .

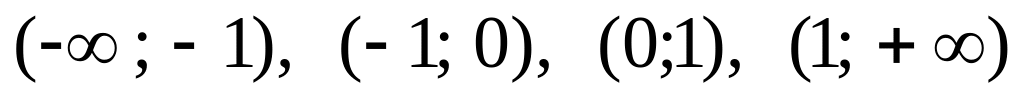4. Составим таблицу II, знак второй производной на интервалах выпуклости и вогнутости определить по ее знаку в произвольной точке интервалов.

			0			▼
	–	+	0	–	+

Пример 8. Найти интервалы выпуклости, вогнутости и точки перегиба функции .

1. ▲ Область определения функции .

2. Найдем производные: .

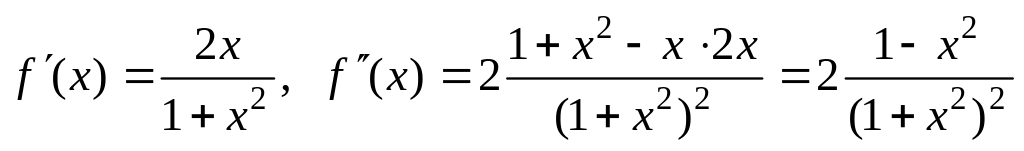3. Вторая производная функции существует 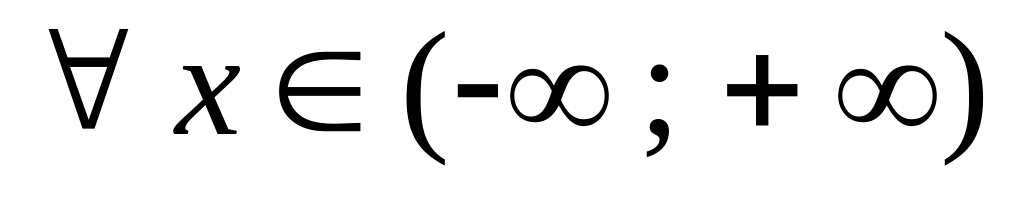. и 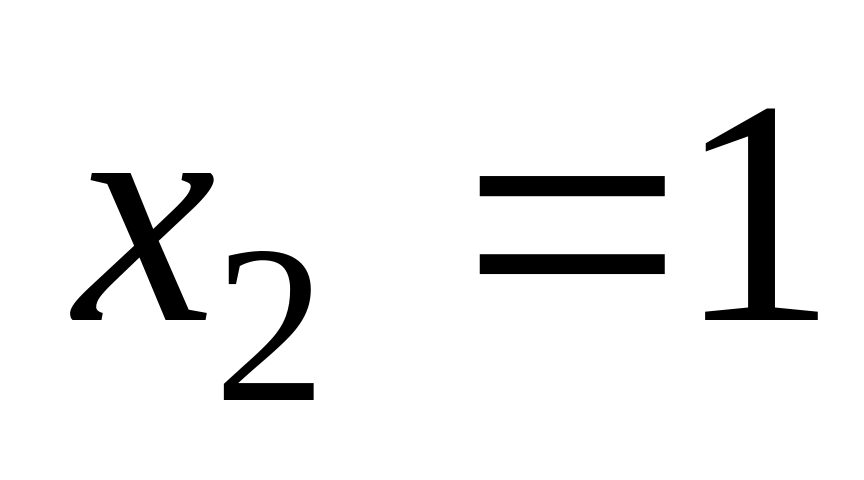. Критические точки второго рода 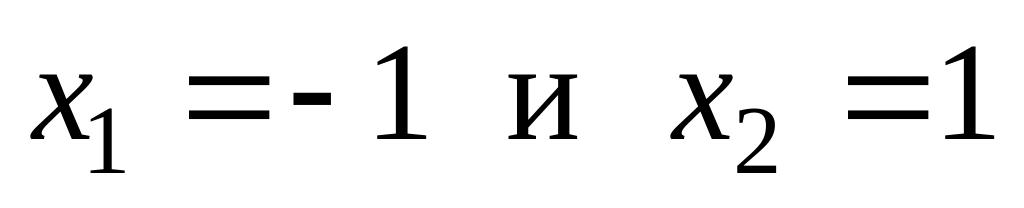. Разобьем область определения функции на интервалы .

4. Составим таблицу II, знак второй производной на интервалах выпуклости и вогнутости определить по ее знаку в произвольной точке интервалов.

		–1		1		▼
	–	0	+	0	–

Пример 9. Найти интервалы выпуклости, вогнутости и точки перегиба функции .

1. ▲ Область определения функции .

2. Найдем производные:

, .

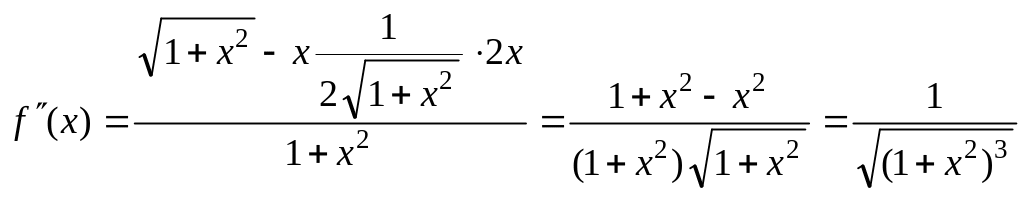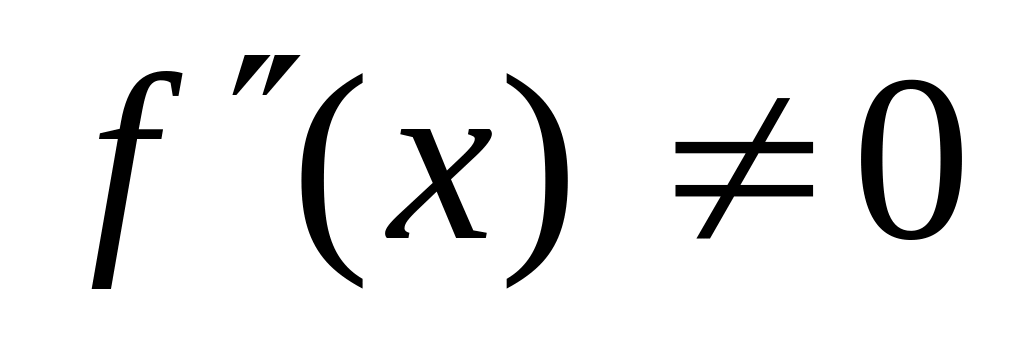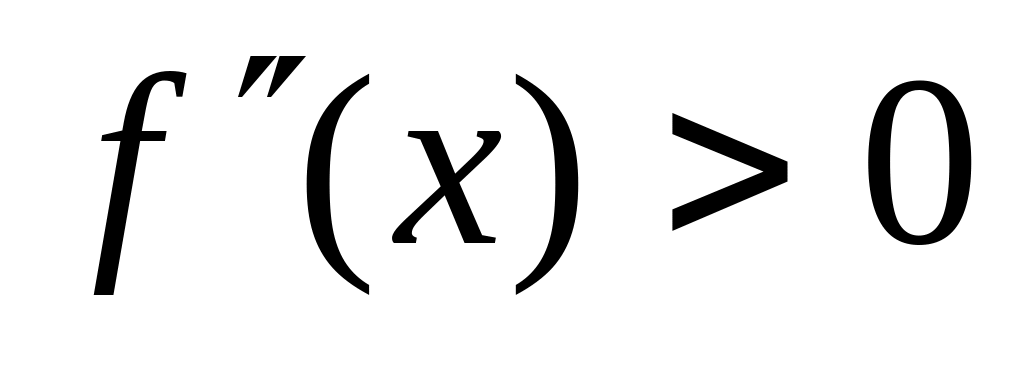3. Вторая производная функции существует . Вторая производная . Критических точек второго рода нет, поэтому нет точек перегиба (не выполнен необходимый признак). Так как , то график функции выпуклый вниз. ▼