3. Асимптоты графика функции

Может оказаться, что размеры графика данной функции , не ограничены. Это бывает, когда функция не ограничена или когда она задана на неограниченном промежутке. В таких случаях часто представление о графике функции вне рамок чертежа дают асимптоты графика.

Определение. Прямая называется асимптотой кривой , если расстояние от точки кривой до прямой стремится к нулю при неограниченном удалении точки по какой-либо части кривой от начала координат.

Различают три вида асимптот: вертикальные (параллельные оси ), горизонтальные (параллельные оси ) и наклонные (не параллельные ни одной из координатных осей).

Прямая является вертикальной асимптотой графика функции , если выполнено хотя бы одно из условий

.

Для разыскания вертикальных асимптот кривой поступаем следующим образом:

1. находим на оси точки разрыва функции ;

2. выделяем те из них, в которых хотя бы один из пределов функции (слева или справа) равен . Пусть это будут точки . Тогда прямые будут вертикальными асимптотами графика функции .

Наклонные асимптоты

Теорема 4. Для того чтобы график функции имел наклонную асимптоту , необходимо и достаточно, чтобы существовали оба предела

.

Аналогично для случая .

Горизонтальная асимптота (частный случай наклонной асимптоты )

Если функция имеет конечный предел, равный числу : , то прямая есть горизонтальная асимптота соответственно для правой или левой ветви графика функции .

Правило отыскания асимптот очевидно из следующего образца.

Пример 10. Найти асимптоты кривой .

1. ▲ Найдем область определения функции: .

.

Функция не определена в точках . Определим тип разрыва в этих точках, для чего вычислим пределы ,

,

,

.

Следовательно, прямые вертикальные асимптоты.

2. Найдем левую наклонную асимптоту:

;

.

Следовательно, имеем слева горизонтальную асимптоту .

Найдем правую наклонную асимптоту:

;

.

Значит, справа имеем горизонтальную асимптоту .

▼

Пример 11. Найти асимптоты кривой .

1. ▲ Найдем область определения функции: . Функция не определена в точке . Определим тип разрыва в этой точке, для чего вычислим пределы

Аналогично получаем .

Прямая – вертикальная асимптота.

2. Для нахождения левой наклонной асимптоты вычислим

,

.

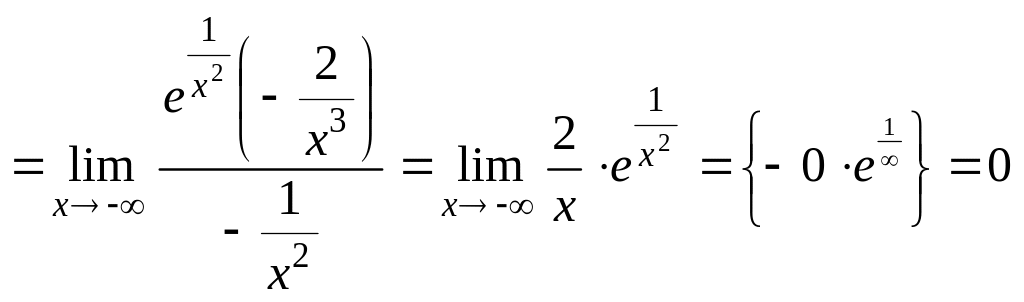Следовательно, прямая – левая наклонная асимптота.

Аналогично для правой наклонной асимптоты получаем

.

Следовательно, прямая – наклонная асимптота.

▼

Пример 12. Найти асимптоты кривой .

1. ▲ Найдем область определения функции: . Поэтому вертикальная асимптота может существовать лишь на конечной границе области определения. Найдем

.

Значит, прямая – вертикальная асимптота.

2. Найдем правую наклонную асимптоту (так как ):

.

.

Следовательно, наклонной асимптоты нет.

▼