Особливість

Якщо дискретні випадкові величини   мають нормальний розподіл імовірностей, то їх сума    різниця   також будуть нормально розподілені, а добуток   величин   не буде підпорядкований нормальному розподілу

18. Критерій Пірсона, чи критерій χ ² (Хі-квадрат) - найбільш часто вживається критерій для перевірки гіпотези про закон розподілу. У багатьох практичних завданнях точний закон розподілу невідомий, тобто є гіпотезою, яка вимагає статистичної перевірки.Позначимо через X досліджувану випадкову величину. Нехай потрібно перевірити гіпотезу про те, що ця випадкова величина підкоряється закону розподілу F(x). Для перевірки гіпотези зробимо вибірку, що складається з n незалежних спостережень над випадковою величиною X. За вибіркою можна побудувати емпіричне розподіл F*(x) досліджуваної випадкової величини. Порівняння емпіричного розподілу F*(x) і теоретичного (або, точніше було б сказати, гіпотетичного - тобто відповідного гіпотезі ) розподілу F(x)проводиться за допомогою спеціального правила - критерію згоди. Одним з таких критеріїв і є критерій Пірсона.

19. t-критерій Стьюдента - загальна назва для класу методів статистичної перевірки гіпотез (статистичних критеріїв), заснованих на розподілі Стьюдента. Найбільш часті випадки застосування t-критерію пов'язані з перевіркою рівності середніх значень у двох вибірках.

t-статистика будується зазвичай за таким загальним принципом: в чисельнику випадкова величина з нульовим математичним очікуванням (при виконанні нульової гіпотези), а в знаменнику - вибіркове стандартне відхилення цієї випадкової величини, одержуване як квадратний корінь з незміщеної оцінки дисперсії.

Для застосування даного критерію необхідно, щоб вихідні дані мали нормальний розподіл. У разі застосування двохвибіркового критерію для незалежних вибірок також необхідне дотримання умови рівності дисперсій. Існують, проте, альтернативи критерію Стьюдента для ситуації з нерівними дисперсіями.

Вимога нормальності розподілу даних є необхідним для точного t-тесту. Однак, навіть при інших розподілах даних можливе використання t-статистики. У багатьох випадках ця статистика асимптотично має стандартний нормальний розподіл –N(0,1), тому можна використовувати квантилі цього розподілу. Однак, часто навіть у цьому випадку використовують квантилі не стандартного нормального розподілу, а відповідного розподілу Стьюдента, як у точній t-тесті. Асимптотично вони еквівалентні, проте на малих вибірках довірчі інтервали розподілу Стьюдента ширше й надійніше.

Одновиборочний t-критерій

Застосовується для перевірки нульової гіпотези про рівність математичного очікування деякого відомому значенню m.

Очевидно, при виконанні нульової гіпотези . З урахуванням передбачуваної незалежності спостережень . Використовуючи несмещенную оцінку дисперсії отримуємо наступну t-статистику:

При нульовій гіпотезі розподіл цієї статистики . Отже, при перевищенні критичного значення нульова гіпотеза відкидається.

Двухвиборочний t-критерій для незалежних вибірок

Нехай є дві незалежні вибірки обсягами нормально розподілених випадкових величин X1,X2. Необхідно перевірити за вибірковими даними нульову гіпотезу рівність математичних сподівань цих випадкових величин.

Розглянемо різницю вибіркових середніх . Очевидно, якщо нульова гіпотеза виконана . Дисперсія цієї різниці дорівнює виходячи з незалежності вибірок: . Тоді використовуючи несмещенную оцінку дисперсії отримуємо несмещенную оцінку дисперсії різниці вибіркових середніх: . Отже, t-статистика для перевірки нульової гіпотези дорівнює

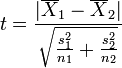
Ця статистика при справедливості нульової гіпотези має розподіл , де

Випадок однакової дисперсії.У випадку, якщо дисперсії вибірок передбачаються однаковими, то . Тоді t-статистика дорівнює:

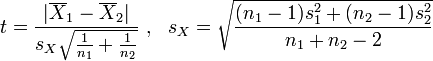
Ця статистика має розподіл

Двохвибірковий t-критерій для залежних вибірок

Для обчислення емпіричного значення t-критерію в ситуації перевірки гіпотези про відмінності між двома залежними вибірками (наприклад, двома пробами одного і того ж тесту з тимчасовим інтервалом) застосовується наступна формула:

де - середня різниця значень, - стандартне відхилення різниць, а n - кількість спостережень Ця статистика має розподіл.

20. Розподіл Фішера або F-розподіл у теорії імовірностей — двопараметричне сімейство абсолютно неперервних розподілів. F-розподіл часто зустрічається як розподіл тестової статистики коли нульова гіпотеза вірна, особливо в тесті відношення правдоподібності, найважливіший випадок аналіз дисперсії .

Нехай — дві незалежні випадкові величини, що мають розподіл хі-квадрат : Тоді розподіл випадкової величини

називається розподілом Фішера зі ступенями свободи і . Пишуть .

Щільність випадкової величини з F-розподілом з параметрами задається формулою:

.

Математичне чекання і дисперсія випадкової величини, що має розподіл Фішера, мають вигляд: