31.Порівняння дисперсій двох нормальних генеральних сукупностей. Пошук критичних областей в залежності від альтернативної гіпотези. Приклади.

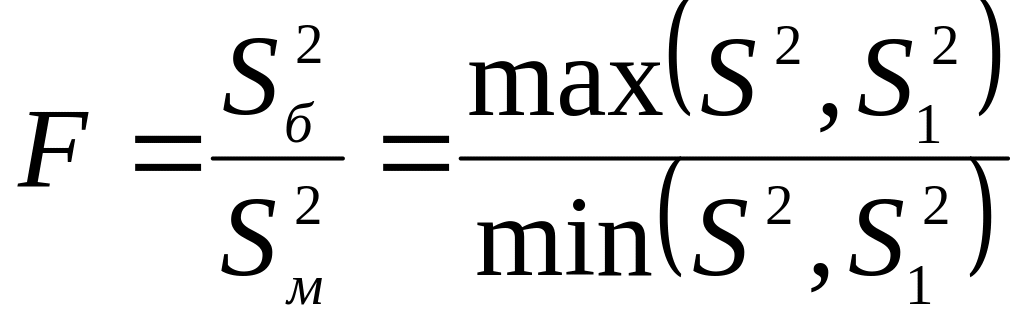Перевіримо гіпотезу про рівність дисперсій: . За критерій перевірки нульової гіпотези вибираємо випадкову величину , яка у разі справедливості має розподіл Фішера з степенями свободи. Спостережуване значення критерію: .

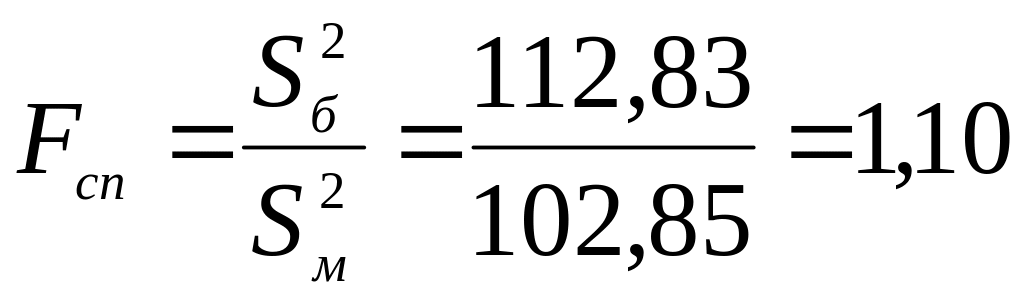1) При альтернативній гіпотезі маємо правобічну критичну область, критична точка шукається за таблицею розподілу Фішера: . В результаті , приймається.

2) При альтернативній гіпотезі маємо двобічну симетричну критичну область, критична точка шукається за таблицею розподілу Фішера: . В результаті , приймається.

32.Порівняння математичних сподівань двох нормально розподілених незалежних генеральних сукупностей з вибірками великого об'єму. Пошук критичних областей в залежності від альтернативної гіпотези. Приклади.

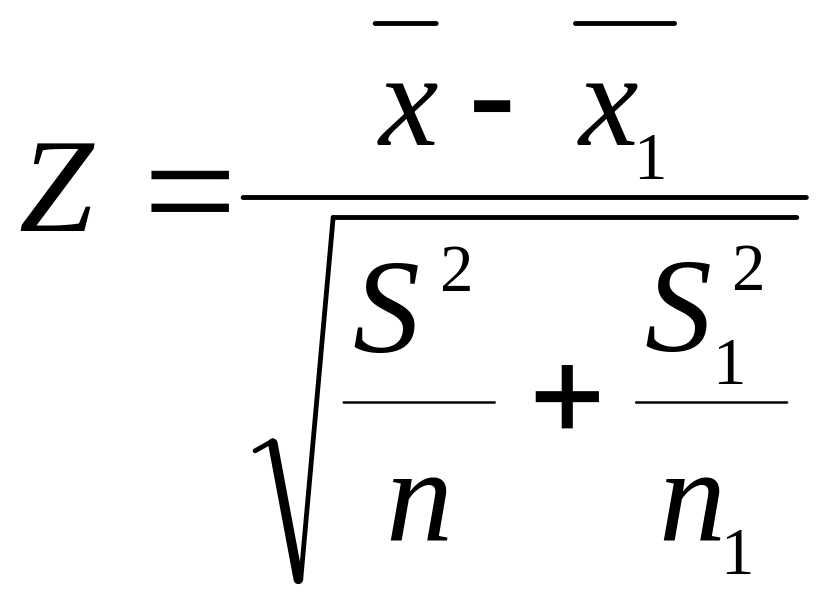Перевіримо гіпотезу про рівність математичних сподівань нормальних генеральних сукупностей і при рівні значущості , вважаючи, що дані вибірки – незалежні і досить великого обсягу. Висуваємо гіпотезу . За критерій перевірки нульової гіпотези вибираємо випадкову величину , яка у разі справедливості має нормальний розподіл. Спостережуване значення критерію: .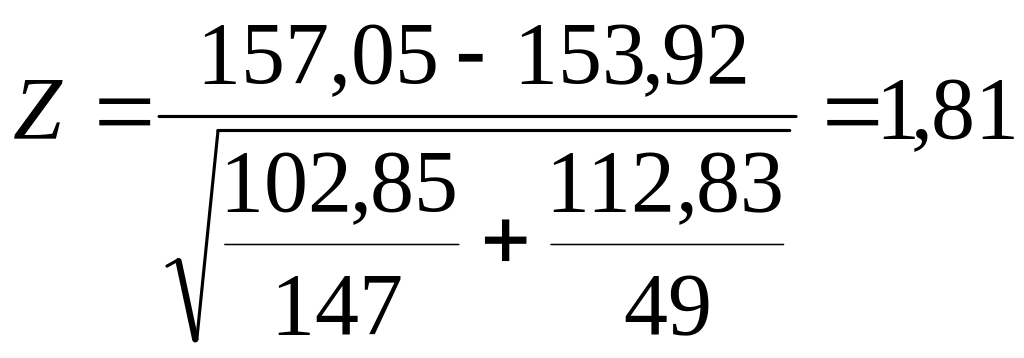

1) При альтернативній гіпотезі маємо правобічну критичну область, критична точка шукається за таблицею нормального розподілу: , звідси . В результаті , відхиляється.

2) При альтернативній гіпотезі маємо лівобічну критичну область, критична точка шукається за таблицею нормального розподілу: , звідси . В результаті , приймається.

3) Якщо альтернативна гіпотеза , то критична область – двобічна симетрична, критична точка шукається за таблицею нормального розподілу: , звідси . В результаті , відхиляється.

33.Порівняння математичних сподівань двох нормально розподілених генеральних сукупностей з однаковими дисперсіями. Пошук критичних областей в залежності від альтернативної гіпотези. Приклади.

знаючи, що з заданим рівнем значущості дисперсії генеральних сукупностей однакові, перевіримо гіпотезу про рівність їх математичних сподівань. Нульова гіпотеза: .

За критерій перевірки вибираємо випадкову величину 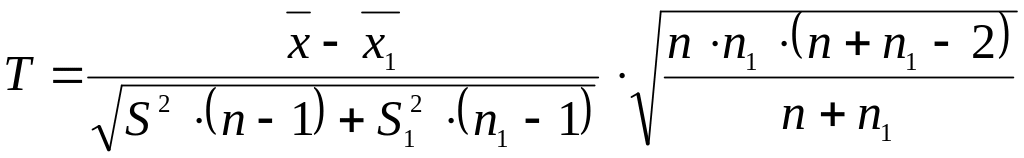, яка у разі справедливості , має розподіл Стьюдента з n+ =194-ма степенями свободи. Спостережуване значення критерію .

1. Якщо альтернативна гіпотеза , шукаємо правобічну критичну область. Критична точка шукається за таблицею розподілу Стьюдента для однобічної області та рівня значущості або за таблицею розподілу Стьюдента для двобічної області та рівня значущості :

.

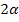, тому відхиляється.

2) Якщо альтернативна гіпотеза шукаємо лівобічну критичну область. Критична точка шукається за таблицею розподілу Стьюдента для однобічної області та рівня значущості або за таблицею розподілу Стьюдента для двобічної області та рівня значущості 2 :

.

, тому приймається.

3) Альтернативна гіпотеза . При висунутій альтернативній гіпотезі шукаємо двобічну критичну область. Вона симетрична відносно початку координат, тому шукаємо тільки одну критичну точку:

, тому приймається.