
- •Методические указания
- •Составитель
- •Рецензент
- •4. Корреляционная функция с.П.
- •8. Стационарные случайные процессы.
- •9. Эргодическое свойство стационарного случайного процесса.
- •10. Спектральное разложение стационарного случайного процесса.
- •11. Преобразование стационарного с.П. Стационарной линейной динамической системой.
- •Решения задач
- •Так как функция – четная, то, доопределив полученную функцию по четности на интервале (; 0), получим.
- •Найдем взаимную корреляционную функцию по свойству 7) п.8
- •Решение. А) Обозначим . Тогда по формуле (5) п. 8 имеем
- •По формуле (5) имеем
- •Решение. По формуле 1) п. 11 найдем математическое ожидание
- •Табличные интегралы
- •Сведения из теории вычетов.
4. Корреляционная функция с.П.
Пусть
![]() центрированный
с.п.
центрированный
с.п.
Корреляционной функцией с.п.X(t) называется неслучайная функция от двух аргументовt1,t2
![]() .
.
Нормированной корреляционной функцией с.п. X(t) называется неслучайная функция
![]() .
.
Свойства корреляционной функции с.п.ПустьX(t)случайный процесс,U случайная величина,φ(t)неслучайная функция.




 .
.
 .
.
 ,
,
 .
.
5. Взаимная корреляционная функция с.п. ПустьX(t),Y(t)случайные процессы.Взаимной корреляционной функцией с. п. X(t),Y(t) называется неслучайная функция от двух аргументовt1,t2
![]() .
.
Два с.п. X(t),Y(t) называютсянекоррелированными, если
![]() .
.
Нормированной взаимной корреляционной функцией с.п. X(t),Y(t) называется неслучайная функция
![]() .
.
Свойства взаимной корреляционной функции.ПустьX(t),Y(t)случайные процессы,φ(t),ψ(t)неслучайные функции.




 .
. .
.
Теорема.Если
![]() ,
то
,
то
![]() .
.
Следствие.Если
![]() и с. п.
и с. п.
![]() попарно некоррелированы, то
попарно некоррелированы, то
![]() .
.
Для
двух случайных процессов
![]() и
и
![]() теорема и следствие выглядят следующим
образом.
теорема и следствие выглядят следующим
образом.
![]() .
(1)
.
(1)
Если с.п.![]() и
и
![]() некоррелированы, то
некоррелированы, то
![]() .
(2)
.
(2)
6.
Характеристики производной случайного
процесса. ПустьX(t)случайный процесс,
![]() его производная. Тогда верны следующие
свойства.
его производная. Тогда верны следующие
свойства.
 .
. .
. ,
,
 .
.
Замечание. Рекомендуем ознакомиться с понятиями предела, производной и интеграла в среднеквадратическом смысле в пособиях /2,5,8/.
7. Характеристики интеграла от случайного процесса.ПустьX(t)случайный процесс,
![]() .
.
Тогда выполняются следующие свойства.
 .
. .
. ,
,
 .
.
8. Стационарные случайные процессы.
С.п.
X(t)
называетсястационарным(в широком
смысле), если его м. о. постоянно, а
корреляционная функция зависит только
от
![]() .
.
Таким образом,
![]() =
const,
(3)
=
const,
(3)
![]() ,
где
,
где
![]() .
(4)
.
(4)
Два
стационарных с.п.X(t)
иY(t)
называютсястационарно связанными,
если взаимно корреляционная функция
![]() ,
где
,
где![]() .
.
Основные свойства и формулы для стационарных с.п. ПустьX(t)стационарный случайный процесс.
 =
const.
=
const. .
. четность функции.
четность функции. ,
где
,
где
 нормированная корреляционная функция
с.п.X(t).
нормированная корреляционная функция
с.п.X(t).
Характеристики производной стационарного случайного процесса. ПустьX(t)дифференцируемый стационарный с.п. Тогда
 стационарный
случайный процесс.
стационарный
случайный процесс. .
.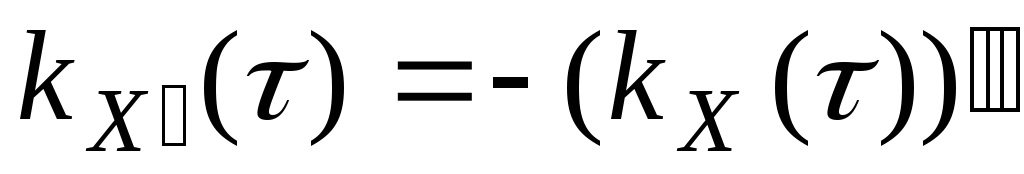 .
. ,
,
 –
– и
и стационарно связаны
стационарно связаны
Характеристики
интеграла от стационарного случайного
процесса. ПустьX(t)интегрируемый стационарный с.п. и
![]() .
Тогда
.
Тогда
 .
. .
. ,
,
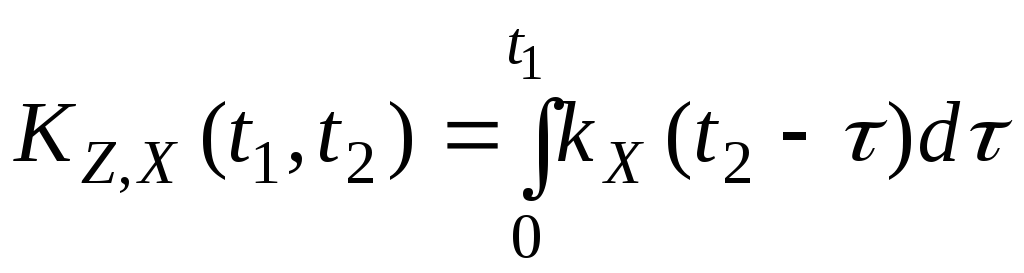 .
.
Рассмотрим
функцию![]() .
Тогда по свойству 9) имеем
.
Тогда по свойству 9) имеем
![]() .
(5)
.
(5)
Заметим,
что функция I(t)
– четная, а для функции
![]() выполняется
соотношение
выполняется
соотношение
![]() .
Это можно доказать, сделав замену
переменной
= –s
в обоих интегралах I(–t)
и
.
Это можно доказать, сделав замену
переменной
= –s
в обоих интегралах I(–t)
и
![]() .
.
9. Эргодическое свойство стационарного случайного процесса.
Определение.
Стационарный с.п. X(t)
называетсяэргодическим относительно
математического ожиданияmX
, если для любой его реализации![]()
![]() .
(6)
.
(6)
Стационарный
с.п X(t)
называетсяэргодическим относительно
корреляционной функции kX(τ),
если для любой его реализации![]()
![]() .
(7)
.
(7)
