41. Гіпергеометричний закон. Числові характеристики.

Гіпергеометричний розподіл описує ймовірність того, що у вибірці з n різних об'єктів, витягнутих із представлення рівноk об'єктів є бракованими. В загальному, якщо випадкова величина X відповідає гіпергеометричному розподілу з параметрами N, D і n, то ймовірність отримання рівно k успіхів визначається формулою:

Ця ймовірність додатня коли k лежить на проміжку між max{ 0, D + n − N } і min{ n, D }. Наведена формула може трактуватися так: існує   способів заповнити залишок вибірки (без повернення). Є   способів вибрати kбракованих об'єктів і   способів заповнити залишок вибірки об'єктами без дефектів.

42. Закон рівномірного розподілу на проміжку [a,b].

Якщо ймовірність потрапляння випадкової величини на інтервал пропорційна до довжини інтервалу і не залежить від розташування інтервалу на осі, то вона має рівномірний закон розподілу. Щільність такого розподілу:

Рівномірний закон розподілу легко моделювати. За допомогою функціональних перетворень із величин, розподілених рівномірно, можна діставати величини з довільним законом розподілу. Числові характеристики розподілу:

43. Пуассонівський (експоненціальний закон) розподілу неперервної випадкової величини.

В застосуваннях теорії ймовірностей на практиці: в теорії масового обслуговування, в дослідженні операцій, в теорії надійності мають справу з випадковими величинами, які мають експоненціальний закон розподілу.

Випадкова величина x має експоненціальний закон розподілу (показниковий розподіл) із параметром l > 0, якщо вона неперервна та її щільність ймовірностей має такий вигляд:

 

 

Тоді функція розподілу ймовірностей буде така:

 (x > 0).

 

Таким чином,

 

44. Нормальний закон розподілу неперервної випадкової величини.

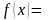
Нормальний закон розподілу задається щільністю Параметри , які входять до виразу щільності розподілу, є відповідно математичним сподіванням та середнім квадратичним відхиленням випадкової величини. Нормальний закон розподілу широко застосовується в математичній статистиці. Для обчислення ймовірності потрапляння випадкової величини, розподіленої нормально, на проміжок використовується функція Лапласа:

Часто застосовується також формула:

45. Ймовірність влучення нормально розподіленої величини в заданий інтервал

Зная плотность распределения, можно вычислить вероятность того, что непрерывная случайная величина примет значение, принадлежащее заданному интервалу. Вычисление основано на следующей теореме.

Теорема. Вероятность того, что непрерывная случайная величина X примет значение, принадлежащее интервалу (а, b), равна определенному интегралу от плотности распределения, взятому в пределах от а до b:

Р(а<Х<b) =

Доказательство. Р(а ≤Х<b) = F(b) — F(a).

По формуле Ньютона — Лейбница,

F(b) — F(a)= .

Таким образом,

Р(а 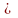Х<b) =

Так как Р(а ≤Х<b) = Р(а<Х<b),то окончательно получим

Р(а<Х<b) =

Геометрически полученный результат можно истолковать так: вероятность того, что непрерывная случайная величина примет значение, принадлежащее интервалу (а,b), равна площади криволинейной трапеции, ограниченной осью Ох, кривой распределения f (х) и прямыми х =а и х=b.

Замечание. В частности, если f (х) — четная функция и концы интервала симметричны относительно начала координат, то

Р(-а<Х<a) = Р(|Х|<a) =2