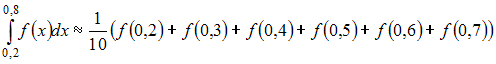12.1.Интерполирование функций: интерполяционные полиномы Лагранжа
Интерполяционный
многочлен Лагранжа, составленный по
таблице значений функции
имеет
вид …
|
|
|
|
Функция
представлена
таблицей:
Тогда
в интерполяционном полиноме Лагранжа
2-ой степени с узлами
,
составленном по этой таблице для
приближенного вычисления
при
условии
значение
не
может быть равно
…
|
|
|
8 |
Интерполяционный
многочлен Лагранжа, составленный по
таблице значений функции
имеет
вид …
|
|
|
|
Функция
представлена
таблицей
Тогда
значение
,
вычисленное с помощью интерполяционного
многочлена Лагранжа, равно …
|
|
|
– 3 |
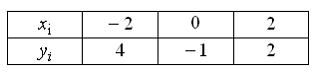
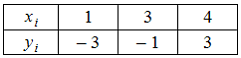
Функция
представлена
таблицей
Тогда
значение
,
вычисленное с помощью интерполяционного
многочлена Лагранжа, равно …
|
|
|
3 |
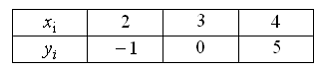
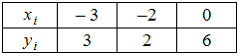
Функция
представлена
таблицей:
Тогда
график многочлена, интерполирующего
эту функцию, пересекает ось
в
точке с абсциссой …
|
|
|
5,5 |
Интерполяционный
многочлен Лагранжа второй степени
может
быть составлен по таблице значений
функции
вида
…
|
|
|
|
Интерполяционный
многочлен Лагранжа, составленный по
таблице значений функции
имеет
вид …
|
|
|
|
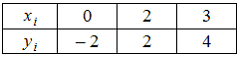
Функция
представлена
таблицей
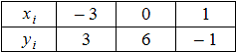Тогда
значение
,
вычисленное с помощью интерполяционного
многочлена Лагранжа, равно …
|
|
|
8 |
Интерполяционный
многочлен Лагранжа второй степени
может
быть составлен по таблице значений
функции
вида
…
|
|
|
|
12.2.Численное дифференцирование и интегрирование
Значение
дифференцируемой функции
в
точке
можно
приближенно найти как …
|
|
|
|
Значение
дифференцируемой функции
в
точке
можно
приближенно найти как …
|
|
|
|
Значение
дифференцируемой функции
в
точке
можно
приближенно найти как …
|
|
|
|
Значение
дифференциала функции
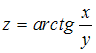в
точке
равно
…
|
|
|
|
Метод
левых прямоугольников дает приближенное
значение интеграла
…
|
|
|
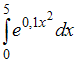с недостатком |
Значение
определенного интеграла
по
формуле парабол (Симпсона) можно
приближенно найти как …
|
|
|
|
Значение определенного интеграла по формуле трапеций можно приближенно найти как …
|
|
|
|
Значение
определенного интеграла
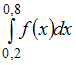по
формуле прямоугольников можно приближенно
найти как …
|
|
|
|
На
рисунке
изображена
геометрическая интерпретация приближенного
вычисления определенного интеграла
методом …
|
|
|
трапеций |
Значение
дифференцируемой функции
в
точке
можно
приближенно найти как …
|
|
|
|
