11.1.Статистическое распределение выборки

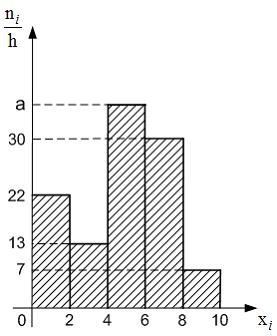Из генеральной совокупности извлечена выборка объема , гистограмма частот которой имеет вид: Тогда значение a равно …

38

Статистическое распределение выборки имеет вид Тогда значение относительной частоты равно …

0,25

Из генеральной совокупности извлечена выборка объем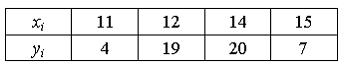а : Тогда несмещенная оценка математического ожидания равна …

13,14

Из генеральной совокупности извлечена выборка объема : 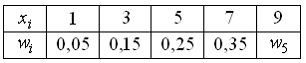Тогда частота варианты в выборке равна …

28

Статистическое распределение выборки имеет вид Тогда объем выборки равен …

67

Из генеральной совокупности извлечена выборка объема : Тогда относительная частота варианты равна …

0,25

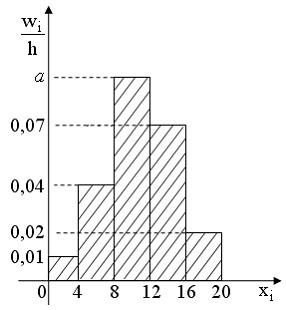Из генеральной совокупности извлечена выборка объема , гистограмма относительных частот которой имеет вид Тогда значение a равно …

Из генеральной совокупности извлечена выборка объема , полигон частот которой имеет вид: 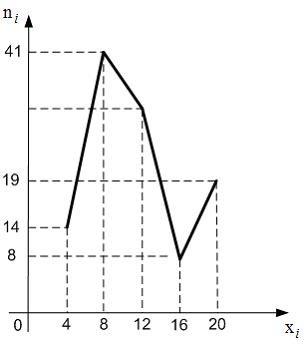Тогда число вариант в выборке равно …

32

Из генеральной совокупности извлечена выборка объема : Тогда значение равно …

34

Из генеральной совокупности извлечена выборка объема , полигон частот которой имеет вид: 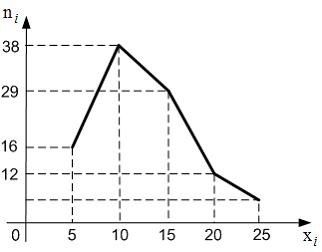Тогда относительная частота варианты в выборке равна …

0,05

11.2.Точечные оценки параметров распределения

В результате измерений некоторой физической величины одним прибором (без систематических ошибок) получены следующие результаты (в мм): 3,6; 3,8; 4,3. Тогда несмещенная оценка дисперсии равна …

0,13

Проведено четыре измерения (без систематических ошибок) некоторой случайной величины (в мм): 8, 9, , 12. Если несмещенная оценка математического ожидания равна 10, то выборочная дисперсия будет равна …

2,5

Проведено пять измерений (без систематических ошибок) некоторой случайной величины (в мм): 4,5; 5,2; 6,1; 7,8, 8,3. Тогда несмещенная оценка математического ожидания равна …

6,38

Из генеральной совокупности извлечена выборка объема : 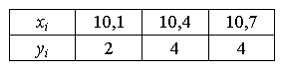Тогда выборочное среднее квадратическое отклонение равно …

Проведено пять измерений (без систематических ошибок) некоторой случайной величины (в мм): 2,1; 2,3; ; 2,7; 2,9. Если несмещенная оценка математического ожидания равна 2,48, то равно …

2,4

Из генеральной совокупности извлечена выборка объема : Тогда несмещенная оценка математического ожидания равна …

13,14

Если все варианты исходного вариационного ряда увеличить в два раза, то выборочная дисперсия …

увеличится в четыре раза

В результате измерений некоторой физической величины одним прибором (без систематических ошибок) получены следующие результаты (в мм): 15; 18; 21; 24. Тогда выборочная дисперсия равна …

11,25

Из генеральной совокупности извлечена выборка объем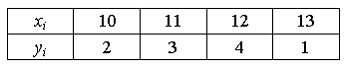а : Тогда выборочная дисперсия равна …

0,84

По выборке объема найдена выборочная дисперсия . Тогда исправленное среднее квадратическое отклонение равно …

2,0