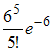- •1)Тема: Прямая на плоскости
- •1)Тема: Плоскость в пространстве
- •1)Тема: Поверхности второго порядка
- •10.1.Определение вероятности
- •10.2.Полная вероятность. Формулы Байеса
- •10.3.Законы распределения вероятностей дискретных случайных величин
- •10.4.Числовые характеристики случайных величин
- •11.1.Статистическое распределение выборки
- •11.2.Точечные оценки параметров распределения
- •11.3.Интервальные оценки параметров распределения
- •11.4.Элементы корреляционного анализа
- •12.1.Интерполирование функций: интерполяционные полиномы Лагранжа
- •12.2.Численное дифференцирование и интегрирование
- •12.3.Численные методы решения дифференциальных уравнений и систем
10.3.Законы распределения вероятностей дискретных случайных величин
Дискретная
случайная величина
![]() задана
законом распределения вероятностей:
задана
законом распределения вероятностей:
 Тогда
вероятность
Тогда
вероятность
![]() равна
…
равна
…
|
|
|
0,8 |
Для
дискретной случайной величины
:
 функция
распределения вероятностей имеет
вид:
функция
распределения вероятностей имеет
вид:
 Тогда
значение параметра
Тогда
значение параметра
![]() может
быть равно …
может
быть равно …
|
|
|
0,7 |
Дискретная
случайная величина
![]() задана
законом распределения вероятностей:
задана
законом распределения вероятностей:
 Тогда
ее функция распределения вероятностей
имеет вид …
Тогда
ее функция распределения вероятностей
имеет вид …
|
|
|
|
Дискретная
случайная величина
задана
законом распределения вероятностей:
 Тогда
значения a
и b
могут быть равны …
Тогда
значения a
и b
могут быть равны …
|
|
|
|
Для
дискретной случайной величины
:
 функция
распределения вероятностей имеет
вид:
функция
распределения вероятностей имеет
вид:
 Тогда
значение параметра
может
быть равно …
Тогда
значение параметра
может
быть равно …
|
|
|
0,655 |
Банк выдал пять кредитов. Вероятность того, что кредит не будет погашен в срок, равна 0,1. Тогда вероятность того, что в срок не будут погашены три кредита, равна …
|
|
|
0,0081 |
Дискретная
случайная величина
задана
законом распределения вероятностей:
 Тогда
ее функция распределения вероятностей
имеет вид …
Тогда
ее функция распределения вероятностей
имеет вид …
|
|
|
|
Дискретная
случайная величина
задана
законом распределения вероятностей:
![]() Тогда
вероятность
Тогда
вероятность
![]() равна
…
равна
…
|
|
|
0,5 |
Среднее число заявок, поступающих на предприятие бытового обслуживания за 1 час равно трем. Тогда вероятность того, что за два часа поступит пять заявок можно вычислить как …
|
|
|
|
10.4.Числовые характеристики случайных величин
Дискретная
случайная величина X
задана законом распределения
вероятностей:
 Тогда
ее среднее квадратическое отклонение
равно …
Тогда
ее среднее квадратическое отклонение
равно …
|
|
|
0,80 |
Непрерывная
случайная величина
задана
плотностью распределения вероятностей:
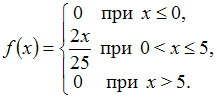 Тогда
ее дисперсия равна …
Тогда
ее дисперсия равна …
|
|
|
|
Непрерывная
случайная величина
задана
функцией распределения вероятностей:
 Тогда
ее дисперсия равна …
Тогда
ее дисперсия равна …
|
|
|
|
Дискретная
случайная величина X
задана законом распределения
вероятностей:
 Тогда
ее математическое ожидание равно …
Тогда
ее математическое ожидание равно …
|
|
|
4,6 |
Дискретная
случайная величина X
задана законом распределения
вероятностей:
 Тогда
ее дисперсия равна …
Тогда
ее дисперсия равна …
|
|
|
7,56 |
Проводится
n
независимых испытаний, в каждом из
которых вероятность появления события
A
постоянна и равна 0,6. Тогда математическое
ожидание
![]() и
дисперсия
и
дисперсия
![]() дискретной
случайной величины X
– числа появлений события A
в
дискретной
случайной величины X
– числа появлений события A
в
![]() проведенных
испытаниях равны …
проведенных
испытаниях равны …
|
|
|
|
Дисперсия
дискретной случайной величины
,
заданной законом распределения
вероятностей:
 равна
0,06. Тогда значение
равна
0,06. Тогда значение
![]() равно
…
равно
…
|
|
|
1,5 |
Непрерывная
случайная величина
задана
плотностью распределения вероятностей
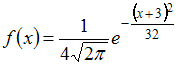 .
Тогда математическое ожидание a
и среднее квадратическое отклонение
.
Тогда математическое ожидание a
и среднее квадратическое отклонение
![]() этой
случайной величины равны …
этой
случайной величины равны …
|
|
|
|
Непрерывная
случайная величина
задана
плотностью распределения вероятностей:
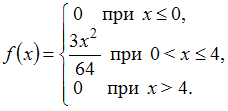 Тогда
ее математическое ожидание равно …
Тогда
ее математическое ожидание равно …
|
|
|
3 |