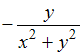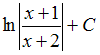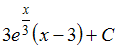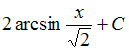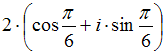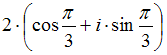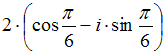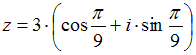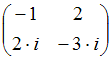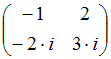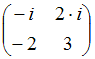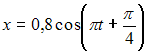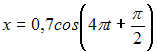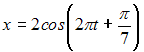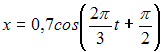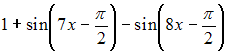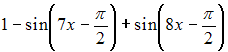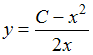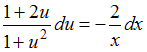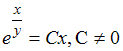- •1)Тема: Прямая на плоскости
- •1)Тема: Плоскость в пространстве
- •1)Тема: Поверхности второго порядка
- •10.1.Определение вероятности
- •10.2.Полная вероятность. Формулы Байеса
- •10.3.Законы распределения вероятностей дискретных случайных величин
- •10.4.Числовые характеристики случайных величин
- •11.1.Статистическое распределение выборки
- •11.2.Точечные оценки параметров распределения
- •11.3.Интервальные оценки параметров распределения
- •11.4.Элементы корреляционного анализа
- •12.1.Интерполирование функций: интерполяционные полиномы Лагранжа
- •12.2.Численное дифференцирование и интегрирование
- •12.3.Численные методы решения дифференциальных уравнений и систем
1)Тема: Поверхности второго порядка
Вершина
параболоида
![]() имеет
координаты …
имеет
координаты …
|
|
|
|
2) Тема: Поверхности второго порядка
Уравнение
геометрического места точек, равноудаленных
от точки
![]() и
от плоскости
и
от плоскости
![]() ,
имеет вид …
,
имеет вид …
|
|
|
|
3) Тема: Поверхности второго порядка
Сфера
с центром
![]() проходит
через точку
проходит
через точку
![]() .
Тогда ее уравнение имеет вид …
.
Тогда ее уравнение имеет вид …
|
|
|
|
4) Тема: Поверхности второго порядка
Даны
уравнения поверхностей второго
порядка:
А)
 B)
B)
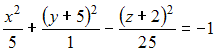 C)
C)
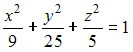 D)
D)
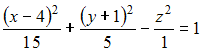 Тогда
двуполостный гиперболоид задается
уравнением …
Тогда
двуполостный гиперболоид задается
уравнением …
|
|
|
B |
5) Тема: Поверхности второго порядка
Уравнение геометрического места точек, равноудаленных от точки и от плоскости , имеет вид …
|
|
|
|
6) Тема: Поверхности второго порядка
Координаты
центра поверхности
![]() равны …
равны …
|
|
|
|
7) Тема: Поверхности второго порядка
Каноническое
уравнение линии пересечения однополостного
гиперболоида
 и
плоскости
и
плоскости ![]() имеет
вид …
имеет
вид …
|
|
|
|
8) Тема: Поверхности второго порядка
Поверхность
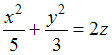 пересекается
с плоскостью
пересекается
с плоскостью
![]() по
…
по
…
|
|
|
параболе |
9) Тема: Поверхности второго порядка
Уравнение геометрического места точек, равноудаленных от точки и от плоскости , имеет вид …
|
|
|
|
10) Тема: Поверхности второго порядка
Вершина параболоида имеет координаты …
|
|
|
|
11) Тема: Поверхности второго порядка
Сфера с центром проходит через точку . Тогда ее уравнение имеет вид …
|
|
|
|
12) Тема: Поверхности второго порядка
Координаты центра поверхности равны …
|
|
|
|
13) Тема: Поверхности второго порядка
Уравнение
поверхности второго порядка ![]() определяет
…
определяет
…
|
|
|
эллипсоид |
14) Тема: Поверхности второго порядка
Центр
сферы
![]() имеет
координаты …
имеет
координаты …
|
|
|
|
15) Тема: Поверхности второго порядка
Вершина параболоида имеет координаты …
|
|
|
|
16) Тема: Поверхности второго порядка
Уравнение
сферы имеет вид
![]() .
Тогда радиус сферы равен …
.
Тогда радиус сферы равен …
|
|
|
7 |
17) Тема: Поверхности второго порядка
Сфера с центром проходит через точку . Тогда ее уравнение имеет вид …
|
|
|
|
18) Тема: Поверхности второго порядка
Даны уравнения поверхностей второго порядка: А) B) C) D) Тогда двуполостный гиперболоид задается уравнением …
|
|
|
B |
19) Тема: Поверхности второго порядка
Уравнение геометрического места точек, равноудаленных от точки и от плоскости , имеет вид …
|
|
|
|
20) Тема: Поверхности второго порядка
Уравнение поверхности второго порядка определяет …
|
|
|
эллипсоид |
21) Тема: Поверхности второго порядка
Уравнение поверхности второго порядка определяет …
|
|
|
эллипсоид |
22) Тема: Поверхности второго порядка
Центр сферы имеет координаты …
|
|
|
|
23) Тема: Поверхности второго порядка
Каноническое уравнение линии пересечения однополостного гиперболоида и плоскости имеет вид …
|
|
|
|
24) Тема: Поверхности второго порядка
Центр сферы имеет координаты …
|
|
|
|
25) Тема: Поверхности второго порядка
Уравнение поверхности второго порядка определяет …
|
|
|
эллипсоид |
26) Тема: Поверхности второго порядка
Центр сферы имеет координаты …
|
|
|
|
27) Тема: Поверхности второго порядка
Координаты центра поверхности равны …
|
|
|
|
28) Тема: Поверхности второго порядка
Каноническое уравнение линии пересечения однополостного гиперболоида и плоскости имеет вид …
|
|
|
|
29) Тема: Поверхности второго порядка
Центр сферы имеет координаты …
|
|
|
|
30) Тема: Поверхности второго порядка
Уравнение геометрического места точек, равноудаленных от точки и от плоскости , имеет вид …
|
|
|
|
31) Тема: Поверхности второго порядка
Центр сферы имеет координаты …
|
|
|
|
32) Тема: Поверхности второго порядка
Вершина параболоида имеет координаты …
|
|
|
|
33) Тема: Поверхности второго порядка
Сфера с центром проходит через точку . Тогда ее уравнение имеет вид …
|
|
|
|
34) Тема: Поверхности второго порядка
Уравнение поверхности второго порядка определяет …
|
|
|
эллипсоид |
35) Тема: Поверхности второго порядка
Уравнение геометрического места точек, равноудаленных от точки и от плоскости , имеет вид …
|
|
|
|
36) Тема: Поверхности второго порядка
Координаты центра поверхности равны …
|
|
|
|
37) Тема: Поверхности второго порядка
Сфера с центром проходит через точку . Тогда ее уравнение имеет вид …
|
|
|
|
Тема: Непрерывность функции, точки разрыва
Для
функции
 точка
точка
![]() является
точкой …
является
точкой …
|
|
|
разрыва первого рода |
Тема: Непрерывность функции, точки разрыва
Функция
 непрерывна
на отрезке …
непрерывна
на отрезке …
|
|
|
|
Тема: Непрерывность функции, точки разрыва
Функция
 не
является непрерывной на отрезке …
не
является непрерывной на отрезке …
|
|
|
|
Тема: Непрерывность функции, точки разрыва
Точка
![]() является
точкой разрыва функции …
является
точкой разрыва функции …
|
|
|
|
Тема: Непрерывность функции, точки разрыва
Для
функции
![]() точка
точка
![]() является
точкой …
является
точкой …
|
|
|
разрыва второго рода |
Тема: Непрерывность функции, точки разрыва
Количество
точек разрыва функции
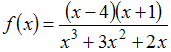 равно
…
равно
…
|
|
|
3 |
Тема: Непрерывность функции, точки разрыва
Точка
разрыва функции
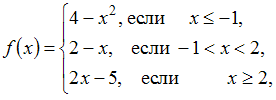 равна
…
равна
…
|
|
|
2 |
Тема: Непрерывность функции, точки разрыва
Количество
точек разрыва функции
 равно
…
равно
…
|
|
|
2 |
Тема: Непрерывность функции, точки разрыва
Функция непрерывна на отрезке …
|
|
|
|
Точка является точкой разрыва функции …
|
|
|
|
Тема: Непрерывность функции, точки разрыва
Точка разрыва функции равна …
|
|
|
2 |
Тема: Непрерывность функции, точки разрыва
Функция не является непрерывной на отрезке …
|
|
|
|
Тема: Непрерывность функции, точки разрыва
Точка
разрыва функции
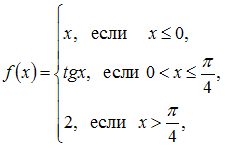 равна
…
равна
…
|
|
|
|
Тема: Непрерывность функции, точки разрыва
Для функции точка является точкой …
|
|
|
разрыва второго рода |
Тема: Непрерывность функции, точки разрыва
Количество точек разрыва функции равно …
|
|
|
3 |
Тема: Непрерывность функции, точки разрыва
Для функции точка является точкой …
|
|
|
разрыва первого рода |
Тема: Непрерывность функции, точки разрыва
Функция непрерывна на отрезке …
|
|
|
|
Тема: Непрерывность функции, точки разрыва
Количество
точек разрыва функции
 равно
…
равно
…
|
|
|
4 |
Тема: Непрерывность функции, точки разрыва
Точка является точкой разрыва функции …
|
|
|
|
Тема: Непрерывность функции, точки разрыва
Количество точек разрыва функции равно …
|
|
|
3 |
Тема: Непрерывность функции, точки разрыва
Точка разрыва функции равна …
|
|
|
2 |
Тема: Непрерывность функции, точки разрыва
Количество точек разрыва функции равно …
|
|
|
3 |
Тема: Непрерывность функции, точки разрыва
Функция непрерывна на отрезке …
|
|
|
|
Тема: Дифференциальное исчисление ФНП
Приближенное
значение функции
![]() в
точке
в
точке
![]() ,
вычисленное с помощью полного
дифференциала, равно …
,
вычисленное с помощью полного
дифференциала, равно …
|
|
|
|
Тема: Дифференциальное исчисление ФНП
Частная
производная
![]() функции
функции
![]() имеет
вид …
имеет
вид …
|
|
|
|
Тема: Дифференциальное исчисление ФНП
Частная
производная второго порядка
![]() функции
функции
![]() имеет
вид …
имеет
вид …
|
|
|
|
Тема: Дифференциальное исчисление ФНП
Частная
производная
![]() функции
функции
![]() имеет
вид …
имеет
вид …
|
|
|
|
Тема: Дифференциальное исчисление ФНП
Полный
дифференциал функции
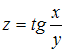 имеет
вид …
имеет
вид …
|
|
|
|
Тема: Дифференциальное исчисление ФНП
Приближенное
значение функции
![]() в
точке
в
точке
![]() ,
вычисленное с помощью полного
дифференциала, равно …
,
вычисленное с помощью полного
дифференциала, равно …
|
|
|
|
Тема: Дифференциальное исчисление ФНП
Частная
производная
![]() функции
функции
![]() имеет
вид …
имеет
вид …
|
|
|
|
Тема: Дифференциальное исчисление ФНП
Значение
частной производной
функции
 в
точке
в
точке
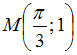 равно
…
равно
…
|
|
|
|
Тема: Дифференциальное исчисление ФНП
Частная производная функции имеет вид …
|
|
|
|
Тема: Дифференциальное исчисление ФНП
Частная производная функции имеет вид …
|
|
|
|
Тема: Дифференциальное исчисление ФНП
Смешанная
частная производная второго порядка
![]() функции
функции
![]() имеет
вид …
имеет
вид …
|
|
|
|
Тема: Дифференциальное исчисление ФНП
Приближенное значение функции в точке , вычисленное с помощью полного дифференциала, равно …
|
|
|
|
Тема: Дифференциальное исчисление ФНП
Смешанная частная производная второго порядка функции имеет вид …
|
|
|
|
Тема: Дифференциальное исчисление ФНП
Частная
производная второго порядка
![]() функции
функции
![]() имеет
вид …
имеет
вид …
|
|
|
|
Тема: Дифференциальное исчисление ФНП
Частная производная второго порядка функции имеет вид …
|
|
|
|
Тема: Дифференциальное исчисление ФНП
Приближенное значение функции в точке , вычисленное с помощью полного дифференциала, равно …
|
|
|
|
Тема: Дифференциальное исчисление ФНП
Частная производная второго порядка функции имеет вид …
|
|
|
|
Тема: Дифференциальное исчисление ФНП
Полный дифференциал функции имеет вид …
|
|
|
|
Тема: Дифференциальное исчисление ФНП
Смешанная частная производная второго порядка функции имеет вид …
|
|
|
|
Тема: Дифференциальное исчисление ФНП
Частная производная второго порядка функции имеет вид …
|
|
|
|
Тема: Дифференциальное исчисление ФНП
Частная производная второго порядка функции имеет вид …
|
|
|
|
Тема: Дифференциальное исчисление ФНП
Приближенное значение функции в точке , вычисленное с помощью полного дифференциала, равно …
|
|
|
|
Основные методы интегрирования
Множество
первообразных функции
![]() имеет
вид …
имеет
вид …
|
|
|
|
Основные методы интегрирования
Множество
первообразных функции
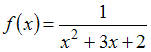 имеет
вид …
имеет
вид …
|
|
|
|
Основные методы интегрирования
Множество
первообразных функции
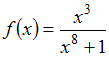 имеет
вид …
имеет
вид …
|
|
|
|
Основные методы интегрирования
Множество
первообразных функции
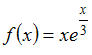 имеет
вид …
имеет
вид …
|
|
|
|
Основные методы интегрирования
Множество первообразных функции имеет вид …
|
|
|
|
Основные методы интегрирования
Множество первообразных функции имеет вид …
|
|
|
|
Основные методы интегрирования
Множество
первообразных функции
![]() имеет
вид …
имеет
вид …
|
|
|
|
Основные методы интегрирования
Множество первообразных функции имеет вид …
|
|
|
|
Основные методы интегрирования
Множество
первообразных функции
 имеет
вид …
имеет
вид …
|
|
|
|
Основные методы интегрирования
Множество
первообразных функции
![]() имеет
вид …
имеет
вид …
|
|
|
|
Основные методы интегрирования
Множество
первообразных функции
![]() имеет
вид …
имеет
вид …
|
|
|
|
Основные методы интегрирования
Множество первообразных функции имеет вид …
|
|
|
|
Основные методы интегрирования
Множество первообразных функции имеет вид …
|
|
|
|
Основные методы интегрирования
Множество первообразных функции имеет вид …
|
|
|
|
Основные методы интегрирования
Множество
первообразных функции
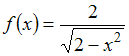 имеет
вид …
имеет
вид …
|
|
|
|
Основные методы интегрирования
Множество первообразных функции имеет вид …
|
|
|
|
Основные методы интегрирования
Множество первообразных функции имеет вид …
|
|
|
|
Основные методы интегрирования
Множество первообразных функции имеет вид …
|
|
|
|
Основные методы интегрирования
Множество
первообразных функции
 имеет
вид …
имеет
вид …
|
|
|
|
Основные методы интегрирования
Множество первообразных функции имеет вид …
|
|
|
|
Основные методы интегрирования
Множество первообразных функции имеет вид …
|
|
|
|
Основные методы интегрирования
Множество первообразных функции имеет вид …
|
|
|
|
Основные методы интегрирования
Множество первообразных функции имеет вид …
|
|
|
|
Основные методы интегрирования
Множество первообразных функции имеет вид …
|
|
|
|
Основные методы интегрирования
Множество первообразных функции имеет вид …
|
|
|
|
Основные методы интегрирования
Множество первообразных функции имеет вид …
|
|
|
|
Основные методы интегрирования
Множество первообразных функции имеет вид …
|
|
|
|
Основные методы интегрирования
Множество первообразных функции имеет вид …
|
|
|
|
Основные методы интегрирования
Множество первообразных функции имеет вид …
|
|
|
|
Тема: Приложения определенного интеграла
Площадь
фигуры, изображенной на рисунке
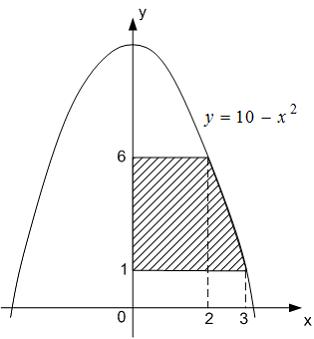 равна
…
равна
…
|
|
|
|
Тема: Приложения определенного интеграла
Площадь
фигуры, изображенной на рисунке
 равна
…
равна
…
|
|
|
|
Тема: Приложения определенного интеграла
Площадь
фигуры, изображенной на рисунке
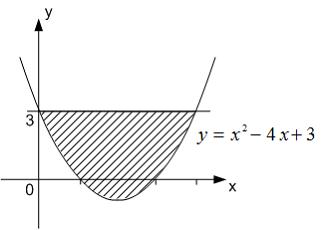 равна
…
равна
…
|
|
|
|
Тема: Приложения определенного интеграла
Площадь
фигуры, ограниченной параболой
![]() и
осью
,
равна …
и
осью
,
равна …
|
|
|
36 |
Тема: Приложения определенного интеграла
Длина
дуги кривой
![]() от
точки
от
точки
![]() до
точки
до
точки
![]() равна
…
равна
…
|
|
|
|
Тема: Приложения определенного интеграла
Площадь
фигуры, изображенной на рисунке
 равна
…
равна
…
|
|
|
|
Тема: Приложения определенного интеграла
Площадь
фигуры, изображенной на рисунке
 равна
…
равна
…
|
|
|
6 |
Тема: Приложения определенного интеграла
Площадь
фигуры, изображенной на рисунке
 равна
…
равна
…
|
|
|
|
Тема: Приложения определенного интеграла
Объем
тела, полученного вращением вокруг оси
криволинейной
трапеции, ограниченной параболой
![]() и
осью
,
равен …
и
осью
,
равен …
|
|
|
|
Тема: Приложения определенного интеграла
Объем
тела, полученного вращением вокруг оси
криволинейной
трапеции, ограниченной параболой
![]() и
осью
,
равен …
и
осью
,
равен …
|
|
|
|
Тема: Приложения определенного интеграла
Площадь фигуры, ограниченной параболой и осью , равна …
|
|
|
36 |
Векторный анализ
1.Норма вектора в евклидовом пространстве
1.1.
Даны
векторы
![]() и
и
![]() ,
угол между которыми равен
,
угол между которыми равен
![]() .
Тогда проекция вектора
.
Тогда проекция вектора
![]() на
вектор
равна
…
на
вектор
равна
…
|
|
|
|
1.2.
Даны
векторы
![]() и
,
угол между которыми равен
и
,
угол между которыми равен
![]() .
Тогда проекция вектора
на
вектор
равна
…
.
Тогда проекция вектора
на
вектор
равна
…
|
|
|
3 |
1.3.
Норма
вектора
![]() в
евклидовом пространстве со стандартным
скалярным произведением равна …
в
евклидовом пространстве со стандартным
скалярным произведением равна …
|
|
|
3 |
1.4.
Норма
вектора
![]() в
евклидовом пространстве со стандартным
скалярным произведением равна …
в
евклидовом пространстве со стандартным
скалярным произведением равна …
|
|
|
6 |
1.5.
Если
![]() и
–
ортогональные векторы из евклидова
пространства со стандартным скалярным
произведением, такие что
и
–
ортогональные векторы из евклидова
пространства со стандартным скалярным
произведением, такие что
![]() ,
,
![]() ,
то норма вектора
,
то норма вектора
![]() равна
…
равна
…
|
|
|
5 |
1.6. Скалярное произведение векторов и равно 5, угол между векторами равен , норма вектора равна 2. Тогда норма вектора равна …
|
|
|
5 |
1.7.
Если
и
–
ортогональные векторы из евклидова
пространства со стандартным скалярным
произведением, такие что
![]() ,
,
то норма вектора
,
,
то норма вектора
![]() равна
…
равна
…
|
|
|
10 |
1.8. Скалярное произведение векторов и равно 8, угол между векторами равен , норма вектора равна 4. Тогда норма вектора равна …
|
|
|
4 |
1.9. Норма вектора в евклидовом пространстве со стандартным скалярным произведением равна …
|
|
|
6 |
1.10.
Даны
векторы
и
,
угол между которыми равен
.
Проекция вектора
на
вектор
равна
![]() .
Тогда норма вектора
равна
…
.
Тогда норма вектора
равна
…
|
|
|
|
2.Векторное произведение векторов
2.1.
Даны
два вектора:
![]() и
и
![]() ,
где
,
где
![]() ,
,
![]() ,
угол между векторами
,
угол между векторами
![]() и
и
![]() равен
равен
![]() .
Тогда площадь треугольника, построенного
на векторах
и
будет
равна …
.
Тогда площадь треугольника, построенного
на векторах
и
будет
равна …
|
|
|
2,5 |
2.2.
Площадь
параллелограмма, построенного на
векторах
![]() и
и
![]() ,
равна …
,
равна …
|
|
|
|
2.3.
Площадь
треугольника, образованного векторами
![]() и
и
![]() ,
равна …
,
равна …
|
|
|
|
2.4.
Даны
два вектора:
![]() и
и
![]() ,
где
,
где
![]() ,
,
![]() ,
угол между векторами
и
равен
.
Тогда модуль векторного произведения
векторов
и
будет
равен …
,
угол между векторами
и
равен
.
Тогда модуль векторного произведения
векторов
и
будет
равен …
|
|
|
21 |
2.5.
Векторное
произведение векторов
![]() и
и
![]() равно
…
равно
…
|
|
|
|
2.6.
Даны
два вектора:
![]() и
и
![]() .
Тогда вектор
.
Тогда вектор
![]() будет
перпендикулярен и вектору
,
и вектору
,
при
будет
перпендикулярен и вектору
,
и вектору
,
при
![]() равном
…
равном
…
|
|
|
|
2.7.
Даны
два вектора:
![]() и
и
![]() ,
где
,
,
где
,
![]() ,
угол между векторами
и
равен
.
Тогда площадь параллелограмма,
построенного на векторах
и
,
будет равна …
,
угол между векторами
и
равен
.
Тогда площадь параллелограмма,
построенного на векторах
и
,
будет равна …
|
|
|
14 |
2.8.
Даны
два вектора:
![]() и
и
![]() .
Тогда вектор
.
Тогда вектор
![]() ,
перпендикулярный и вектору
и
вектору
,
можно представить в виде …
,
перпендикулярный и вектору
и
вектору
,
можно представить в виде …
|
|
|
|
2.9.
Площадь
треугольника с вершинами в точках
![]() ,
,
![]() и
и
![]() равна
…
равна
…
|
|
|
7,5 |
2.10.
Площадь
параллелограмма, построенного на
векторах
![]() и
и
![]() ,
равна …
,
равна …
|
|
|
|
3.Градиент скалярного поля
3.1.
Модуль
градиента скалярного поля
![]() в
точке
в
точке
![]() равен
…
равен
…
|
|
|
|
3.2.
Модуль
градиента скалярного поля
![]() в
точке
в
точке
![]()
![]() равен
7 при
равном
…
равен
7 при
равном
…
|
|
|
|
3.3.
Градиент
скалярного поля
![]() равен
нулевому вектору в точке …
равен
нулевому вектору в точке …
|
|
|
|
3.4.
Градиент
скалярного поля
![]() в
точке
в
точке
![]() равен
…
равен
…
|
|
|
|
3.5.
Модуль
градиента скалярного поля
![]() в
точке
в
точке
![]() равен
5 при
равном
…
равен
5 при
равном
…
|
|
|
|
3.6.
Модуль
градиента скалярного поля
![]() в
точке
в
точке
![]() равен
…
равен
…
|
|
|
3 |
3.7.
Градиент
скалярного поля
![]() в
точке пересечения оси
с
поверхностью
в
точке пересечения оси
с
поверхностью
![]() равен
…
равен
…
|
|
|
|
3.8.
Градиент
скалярного поля
![]() равен
нулевому вектору в точке …
равен
нулевому вектору в точке …
|
|
|
|
3.9.
Модуль
градиента скалярного поля
![]() в
точке пересечения оси
с
поверхностью
в
точке пересечения оси
с
поверхностью
![]() равен
…
равен
…
|
|
|
|
3.10.
Градиент
скалярного поля
![]() в
точке
в
точке
![]() равен
…
равен
…
|
|
|
|
Тема: Элементы теории множеств
Даны
три множества:
![]() ,
,
![]() и
и
![]() .
Тогда число элементов множества
.
Тогда число элементов множества
![]() равно
…
равно
…
|
1
|
Тема: Элементы теории множеств
Даны
два множества:
![]() и
и
![]() .
Тогда количество целых значений
.
Тогда количество целых значений
![]() ,
принадлежащих объединению множеств
и
,
равно …
,
принадлежащих объединению множеств
и
,
равно …
|
8
|
|
Тема: Элементы теории множеств
Даны
три множества:
![]() ,
,
![]() и
и
![]() .
Тогда число элементов множества
.
Тогда число элементов множества
![]() равно
…
равно
…
|
1
|
|
Тема: Элементы теории множеств
Даны
множества:
![]() ,
,
![]() .
Тогда число целых чисел, принадлежащих
их объединению равно …
.
Тогда число целых чисел, принадлежащих
их объединению равно …
|
9
|
|
Тема: Элементы теории множествД
Даны
два множества:
![]() и
и
![]() .
Тогда количество целых значений
,
принадлежащих пересечению множеств
и
,
равно …
.
Тогда количество целых значений
,
принадлежащих пересечению множеств
и
,
равно …
|
4
|
Тема: Элементы теории множествД
Даны
три множества:
![]() ,
,
![]() и
и
![]() .
Тогда число элементов множества
.
Тогда число элементов множества
![]() равно
…
равно
…
|
3
|
|
Тема: Элементы теории множеств
Даны
три множества:
![]() ,
,
![]() и
и
![]() .
Тогда число элементов множества
.
Тогда число элементов множества
![]() равно
…
равно
…
|
2 |
Тема: Элементы теории множеств
Даны
два множества:
![]() и
и
![]() .
Тогда количество целых значений
,
принадлежащих разности множеств
\
,
равно …
.
Тогда количество целых значений
,
принадлежащих разности множеств
\
,
равно …
|
4 |
Тема: Элементы теории множеств
Даны
множества:
![]() и
и
![]() .
Тогда число элементов, принадлежащих
их пересечению равно …
.
Тогда число элементов, принадлежащих
их пересечению равно …
|
3
|
Тема: Мера плоского множества
Мера
плоского множества, изображенного на
рисунке,
 равна
…
равна
…
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
Тема: Мера плоского множества
Мера
плоского множества
![]() равна
…
равна
…
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
0 |
Тема: Мера плоского множества
Мера
плоского множества
![]() равна
…
равна
…
|
|
|
4 |
|
|
|
1 |
|
|
|
2 |
|
|
|
0 |
Тема: Мера плоского множества
Мера
плоского множества
![]() равна
…
равна
…
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
Тема: Мера плоского множества
Мера
плоского множества, изображенного на
рисунке,
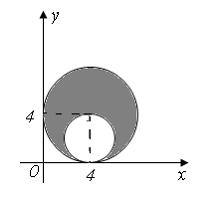 равна
…
равна
…
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
Тема: Мера плоского множества
Мера
плоского множества
![]() ,
где А=
и
,
где А=
и
![]() равна
…
равна
…
|
|
|
|
|
|
|
4 |
|
|
|
0 |
|
|
|
1 |
Тема: Мера плоского множества
Мера
плоского множества
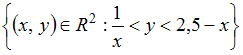 равна
…
равна
…
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
0 |
Тема: Мера плоского множества
Плоская
мера отрезка [0; 1], лежащего на оси
в
плоскости
![]() равна
…
равна
…
|
|
|
0 |
|
|
|
1 |
|
|
|
бесконечности |
|
|
|
несчетна |
Тема: Мера плоского множества
Плоская
мера множества
![]() равна
…
равна
…
|
|
|
0 |
|
|
|
32 |
|
|
|
8 |
|
|
|
18 |
Тема: Отображение множеств
Отображение
![]() действует
по правилу:
действует
по правилу:
 Тогда
Тогда
![]() имеет
вид …
имеет
вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема: Отображение множеств
Отображение,
действующее из отрезка
![]() на
действительную числовую ось и имеющее
обратное отображение, может быть задано
функцией …
на
действительную числовую ось и имеющее
обратное отображение, может быть задано
функцией …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема: Отображение множеств
Прообразом
множества
![]() при
отображении
является
…
при
отображении
является
…
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема: Отображение множеств
Обратимым
на
![]() является
отображение …
является
отображение …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема: Отображение множеств
Образом
отрезка
 при
отображении
при
отображении
![]() является
отрезок …
является
отрезок …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема: Отображение множеств
Отображение
действует
по правилу:
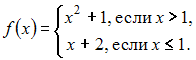 Тогда
имеет
вид …
Тогда
имеет
вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема: Отображение множеств
Пусть
задано отображение
![]() .
Тогда
.
Тогда
![]() имеет
вид …
имеет
вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема: Отображение множеств
Обратимым на является отображение …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема: Отображение множеств
Биективное
отображение отрезка
на
отрезок
![]() может
быть задано функцией …
может
быть задано функцией …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема: Отображение множеств
Пусть
задано отображение
![]() .
Тогда
.
Тогда
![]() представляет
собой …
представляет
собой …
|
|
|
единичную окружность |
|
|
|
отрезок
|
|
|
|
квадрат |
|
|
|
гиперболу |
Тема: Отображение множеств
Прообразом
множества
![]() при
отображении
при
отображении
![]() является
…
является
…
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема: Метрические пространства
Функция
![]() ,
где
,
где
![]() –
действительные числа, …
–
действительные числа, …
|
|
|
удовлетворяет всем трем аксиомам метрического пространства |
|
|
|
не удовлетворяет аксиоме тождества |
|
|
|
не удовлетворяет аксиоме симметрии |
|
|
|
не удовлетворяет аксиоме треугольника |
Тема: Метрические пространства
Функция
![]() ,
где
,
где
![]() и
и
![]()
|
|
|
не удовлетворяет аксиоме треугольника |
|
|
|
не удовлетворяет аксиоме симметрии |
|
|
|
не удовлетворяет аксиоме тождества |
|
|
|
удовлетворяет всем трем аксиомам метрического пространства |
Тема: Метрические пространства
Расстояние
между матрицами
 и
и
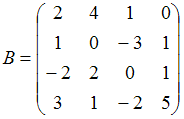 в
метрике
в
метрике
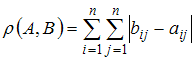 равно
…
равно
…
|
|
|
43 |
|
|
|
13 |
|
|
|
2 |
|
|
|
34 |
Тема: Метрические пространства
Функция
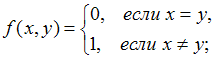 заданная
на множестве целых чисел …
заданная
на множестве целых чисел …
|
|
|
удовлетворяет всем трем аксиомам метрического пространства |
||||||||||||||||
|
|
|
не удовлетворяет аксиоме тождества |
||||||||||||||||
|
|
|
Тема: Метрические пространства Не
может служить
метрикой пространства
|
||||||||||||||||
|
|
|
|
Тема: Метрические пространства
Расстояние
между функциями
![]() и
и
![]() пространства
всех непрерывных действительных функций,
определенных на отрезке
пространства
всех непрерывных действительных функций,
определенных на отрезке
![]() ,
с метрикой
,
с метрикой
![]() ,
равно …
,
равно …
|
|
|
3 |
|
|
|
– 2 |
|
|
|
1 |
|
|
|
|
Тема: Метрические пространства
Расстояние
между точками
![]() и
и
![]() в
метрике
в
метрике
![]() ,
где
и
,
равно …
,
где
и
,
равно …
|
|
|
10 |
|
|
|
1 |
|
|
|
|
|
|
|
– 1 |
Тема: Метрические пространства
Функция
 ,
заданная на множестве натуральных чисел
…
,
заданная на множестве натуральных чисел
…
|
|
|
удовлетворяет всем трем аксиомам метрического пространства |
|
|
|
не удовлетворяет аксиоме тождества |
|
|
|
|
Тема: Метрические пространства
Расстояние
между точками
![]() и
в
метрике
,
где
и
,
равно …
и
в
метрике
,
где
и
,
равно …
|
|
|
4 |
|
|
|
2 |
|
|
|
|
|
|
|
0 |
Тема: Метрические пространства
Функция
![]() ,
где
–
действительные числа, …
,
где
–
действительные числа, …
|
|
|
не удовлетворяет аксиоме симметрии |
|
|
|
не удовлетворяет аксиоме тождества |
|
|
|
удовлетворяет всем трем аксиомам метрического пространства |
|
|
|
не удовлетворяет аксиоме треугольника |
Тема: Комплексные числа и их представление
Тригонометрическая
форма записи комплексного числа
![]() имеет
вид …
имеет
вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема: Комплексные числа и их представление
Комплексное
число задано в показательной форме
![]() Тогда
его тригонометрическая форма записи
имеет вид …
Тогда
его тригонометрическая форма записи
имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема: Комплексные числа и их представление
Модуль
комплексного числа
![]() равен
…
равен
…
|
|
|
2 |
|
|
|
4 |
|
|
|
|
|
|
|
– 1 |
Тема: Комплексные числа и их представление
Главное
значение аргумента комплексного числа
![]() равно
…
равно
…
|
|
|
|
Тема: Комплексные числа и их представление
Комплексное
число задано в тригонометрической форме
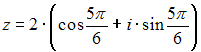 .
Тогда его алгебраическая форма записи
имеет вид …
.
Тогда его алгебраическая форма записи
имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема: Комплексные числа и их представление
Комплексное
число задано в показательной форме
![]() .
Тогда его алгебраическая форма записи
имеет вид …
.
Тогда его алгебраическая форма записи
имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема: Комплексные числа и их представление
Комплексное
число задано в тригонометрической форме
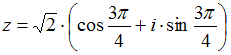 .
Тогда его показательная форма записи
имеет вид …
.
Тогда его показательная форма записи
имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема: Комплексные числа и их представление
Показательная
форма записи комплексного числа
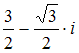 имеет
вид …
имеет
вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема: Комплексные числа и их представление
Комплексное
число задано в тригонометрической форме
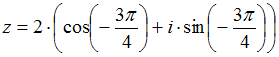 .
Тогда его алгебраическая форма записи
имеет вид …
.
Тогда его алгебраическая форма записи
имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Тригонометрическая
форма комплексного числа имеет вид
![]() ,
а алгебраическая –
,
а алгебраическая –
![]() .
Тогда для нахождения параметров
.
Тогда для нахождения параметров
![]() и
и
![]() получим
систему:
получим
систему:
 В
нашем случае она примет вид:
В
нашем случае она примет вид:
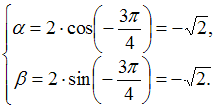 Следовательно,
.
Следовательно,
.

Тема: Дифференцирование функции комплексного переменного
Если
![]() ,
то
,
то
![]() равно
…
равно
…
|
|
|
4 |
|
|
|
0 |
Тема: Комплексные числа и их представление
Комплексное
число задано в показательной форме
![]() .
Тогда его алгебраическая форма записи
имеет вид …
.
Тогда его алгебраическая форма записи
имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема: Системы линейных уравнений с комплексными коэффициентами
Система
 решается
методом Крамера по формулам
,
,
.
Тогда вспомогательный определитель
решается
методом Крамера по формулам
,
,
.
Тогда вспомогательный определитель
![]() равен
…
равен
…
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
Тема: Системы линейных уравнений с комплексными коэффициентами
Если
![]() и
и
![]() являются
решением системы линейных уравнений
являются
решением системы линейных уравнений
 ,
то
,
то
![]() равно
…
равно
…
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
Тема: Системы линейных уравнений с комплексными коэффициентами
Система решается методом Крамера по формулам , , . Тогда вспомогательный определитель равен …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема: Системы линейных уравнений с комплексными коэффициентами
Определитель
системы
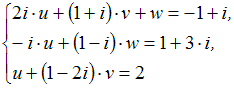 равен
…
равен
…
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема: Системы линейных уравнений с комплексными коэффициентами
Система
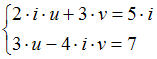 решается
матричным способом по формуле
решается
матричным способом по формуле
![]() ,
где
,
где
![]() ,
–
матрица свободных членов. Тогда
,
–
матрица свободных членов. Тогда
![]() –
матрица, обратная к матрице системы
,
имеет вид …
–
матрица, обратная к матрице системы
,
имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема: Системы линейных уравнений с комплексными коэффициентами
Система
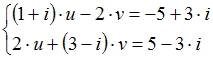 решается
методом Крамера по формулам
,
.
Тогда вспомогательный определитель
решается
методом Крамера по формулам
,
.
Тогда вспомогательный определитель
![]() равен
…
равен
…
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема: Системы линейных уравнений с комплексными коэффициентами
Если
и
являются
решением системы линейных уравнений
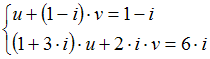 ,
то
,
то
![]() равно
…
равно
…
|
|
|
2 |
|
|
|
|
|
|
|
32 |
|
|
|
0 |
Тема: Системы линейных уравнений с комплексными коэффициентами
Система
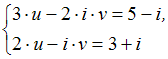 решается
матричным способом по формуле
решается
матричным способом по формуле
![]() ,
где
,
–
матрица свободных членов. Тогда матрица
,
обратная к матрице системы
,
имеет вид …
,
где
,
–
матрица свободных членов. Тогда матрица
,
обратная к матрице системы
,
имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема: Системы линейных уравнений с комплексными коэффициентами
Определитель
системы
 равен
…
равен
…
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема: Системы линейных уравнений с комплексными коэффициентами
Система
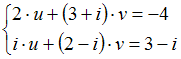 решается
методом Крамера по формулам
,
.
Тогда вспомогательный определитель
равен
…
решается
методом Крамера по формулам
,
.
Тогда вспомогательный определитель
равен
…
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема: Дифференцирование функции комплексного переменного
Если
![]() и
и
![]() ,
то производная функции
,
то производная функции
![]() имеет
вид …
имеет
вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема: Дифференцирование функции комплексного переменного
Если
и
![]() ,
то действительная часть производной
этой функции
,
то действительная часть производной
этой функции
![]() имеет
вид …
имеет
вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема: Дифференцирование функции комплексного переменного
Если
и
![]() ,
то мнимая часть производной этой функции
,
то мнимая часть производной этой функции
![]() имеет
вид …
имеет
вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема: Дифференцирование функции комплексного переменного
Если , то равно …
|
|
|
4 |
|
|
|
0 |
|
|
|
|
|
|
|
|
Тема: Дифференцирование функции комплексного переменного
Значение
производной функции
![]() в
точке
в
точке
![]() равно
…
равно
…
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема: Дифференцирование функции комплексного переменного
Значение
производной функции
![]() в
точке
равно
…
в
точке
равно
…
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема: Дифференцирование функции комплексного переменного
Значение
производной функции
 в
точке
равно
…
в
точке
равно
…
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема: Дифференцирование функции комплексного переменного
Значение
производной функции
![]() в
точке
в
точке
![]() равно
…
равно
…
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема: Дифференцирование функции комплексного переменного
Если
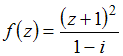 ,
то
,
то
![]() равно
…
равно
…
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
0 |
Тема: Дифференцирование функции комплексного переменного
Если
и
![]() ,
то мнимая часть производной этой функции
имеет
вид …
,
то мнимая часть производной этой функции
имеет
вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема: Периодические функции
Период
функции
![]() равен
…
равен
…
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема: Периодические функции
Период
функции
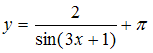 равен
…
равен
…
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема: Периодические функции
Основной
период функции
![]() равен
…
равен
…
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема: Периодические функции
Наименьший
положительный период функции
![]() равен
…
равен
…
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема: Периодические функции
Основной
период функции
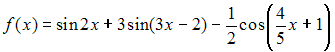 равен
…
равен
…
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема: Периодические функции
Период
функции
![]() равен
…
равен
…
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема: Периодические функции
Наименьший
положительный период функции
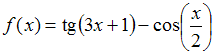 равен
…
равен
…
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема: Периодические функции
Период
функции
![]() равен
…
равен
…
|
|
|
2 |
|
|
|
|
|
|
|
1 |
|
|
|
|
Тема: Периодические функции
Основной
период функции
![]() равен
…
равен
…
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема: Периодические функции
Период
функции
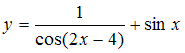 равен
…
равен
…
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема: Гармонические колебания
Гармонические
колебания с частотой 0,5 амплитудой
колебания
![]() и
начальной фазой, равной нулю, описывается
уравнением …
и
начальной фазой, равной нулю, описывается
уравнением …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема: Гармонические колебания
Амплитуда
гармонических колебаний равна
![]() ,
период равен 4 и начальная фаза равна
.
Тогда смещение колеблющейся точки от
нулевого положения при
,
период равен 4 и начальная фаза равна
.
Тогда смещение колеблющейся точки от
нулевого положения при
![]() равно
…
равно
…
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема: Гармонические колебания
Максимальное
значение скорости точки, совершающей
гармонические колебания, с амплитудой
![]() ,
и угловой частотой
,
и угловой частотой
![]() ,
равно …
,
равно …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема: Гармонические колебания
Модуль
скорости точки, совершающей гармонические
колебания, с амплитудой
![]() ,
угловой частотой
,
угловой частотой
![]() и
начальной фазой
и
начальной фазой
![]() ,
в момент времени
,
в момент времени
![]() равен
…
равен
…
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
Тема: Гармонические колебания
Точка
совершает гармонические колебания
вдоль оси
![]() по
закону:
по
закону:
![]() .
Тогда начальная фаза колебаний равна
…
.
Тогда начальная фаза колебаний равна
…
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема: Гармонические колебания
очка
совершает гармонические колебания
вдоль оси
по
закону
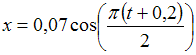 .
Тогда период колебаний равен …
.
Тогда период колебаний равен …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема: Гармонические колебания
Угловая
частота гармонических колебаний равна
![]() ,
начальная фаза
рад,
а смещение колеблющейся точки от нулевого
положения через 2 секунды равно 0,1. Тогда
амплитуда гармонических колебаний
составляет …
,
начальная фаза
рад,
а смещение колеблющейся точки от нулевого
положения через 2 секунды равно 0,1. Тогда
амплитуда гармонических колебаний
составляет …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема: Гармонические колебания
Амплитуда
гармонических колебаний равна
![]() ;
угловая частота равна
рад.;
а начальная фаза равна
.
Тогда смещение колеблющейся точки от
нулевого положения при
составляет
…
;
угловая частота равна
рад.;
а начальная фаза равна
.
Тогда смещение колеблющейся точки от
нулевого положения при
составляет
…
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема: Гармонические колебания
Если
амплитуда гармонических колебаний
равна
![]() и
за 2 минуты совершается 240 колебаний, а
начальная фаза колебаний равна
и
за 2 минуты совершается 240 колебаний, а
начальная фаза колебаний равна
![]() рад,
то уравнение гармонических колебаний
имеет вид …
рад,
то уравнение гармонических колебаний
имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема: Гармонические колебания
Модуль
ускорения точки, совершающей гармонические
колебания, с амплитудой
,
угловой частотой
,
и начальной фазой
,
в момент времени
![]() равен
…
равен
…
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема: Элементы гармонического анализа
Функцией,
ортогональной к функции
![]() на
на
![]() ,
является …
,
является …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема: Элементы гармонического анализа
Функцией,
ортогональной к функции
![]() на
[0,
на
[0,![]() ],
не
является
…
],
не
является
…
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема: Элементы гармонического анализа
Функцией,
ортогональной к функции
![]() на
[-
;
],
не
является
…
на
[-
;
],
не
является
…
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема: Элементы гармонического анализа
Функцией,
ортогональной к функции
![]() на
[-1; 1], является …
на
[-1; 1], является …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема: Элементы гармонического анализа
Функцией,
ортогональной к функции
![]() на
на
 ,
является …
,
является …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема: Элементы гармонического анализа
Функцией,
ортогональной к функции
![]() на
[-
;
],
не
является
…
на
[-
;
],
не
является
…
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема: Элементы гармонического анализа
Функцией,
ортогональной к функции
![]() на
[-1; 1], является …
на
[-1; 1], является …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема: Элементы гармонического анализа
Функцией,
ортогональной к функции
![]() на
на
![]() ,
является …
,
является …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема: Элементы гармонического анализа
Разложение
функции
![]() на
гармоники имеет вид …
на
гармоники имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема: Элементы гармонического анализа
Разложение
функции
![]() на
гармоники имеет вид …
на
гармоники имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема: Ряд Фурье. Теорема Дирихле
Коэффициент
![]() в
разложении в ряд Фурье функции
в
разложении в ряд Фурье функции
![]() на
интервале
на
интервале![]() равен
…
равен
…
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема: Ряд Фурье. Теорема Дирихле
Коэффициент
![]() в
разложении в ряд Фурье функции
в
разложении в ряд Фурье функции
![]() на
интервале
равен
…
на
интервале
равен
…
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема: Ряд Фурье. Теорема Дирихле
Коэффициент
в
разложении
-периодической
функции
![]() ,
,
![]() равен
…
равен
…
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема: Ряд Фурье. Теорема Дирихле
Коэффициент
в
разложении в ряд Фурье функции
![]() равен
…
равен
…
|
|
|
|
|
|
|
|
Тема: Ряд Фурье. Теорема Дирихле
Коэффициент
![]() в
разложении в ряд Фурье функции
в
разложении в ряд Фурье функции
![]() на
интервале
равен
…
на
интервале
равен
…
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема: Ряд Фурье. Теорема Дирихле
Значение
ряда Фурье функции
![]() в
точке
в
точке
![]() равно
…
равно
…
|
|
|
0 |
|
|
|
– 1 |
|
|
|
1 |
|
|
|
|
Тема: Ряд Фурье. Теорема Дирихле
Коэффициент
в
разложении в ряд Фурье функции
![]() на
интервале
равен
…
на
интервале
равен
…
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема: Ряд Фурье. Теорема Дирихле
Коэффициент
в
разложении в ряд Фурье функции
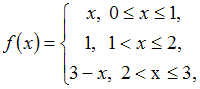 равен
…
равен
…
|
|
|
|
|
|
|
|
Тема: Ряд Фурье. Теорема Дирихле
Коэффициент
в
разложении в ряд Фурье функции
![]() в
ряд косинусов на отрезке
в
ряд косинусов на отрезке
![]() равен
…
равен
…
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
Тема: Ряд Фурье. Теорема Дирихле
Разложение
в ряд Фурье на промежутке
![]() существует
для функции…
существует
для функции…
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Числовые последовательность
Числовая
последовательность задана формулой
общего члена
 .
Тогда значение
.
Тогда значение
![]() равно
равно
|
|
|
|
Тема: Числовые последовательности
Общий
член числовой последовательности
![]() имеет
вид
имеет
вид
|
|
|
|
Числовые последовательности
Из
числовых последовательностей
 ,
,
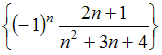 ,
,
 ,
,
 бесконечно
малой не
является
последовательность …
бесконечно
малой не
является
последовательность …
|
|
|
|
Тема: Числовые последовательности
Предел
числовой последовательности
![]() равен
…
равен
…
|
|
|
2 |
Тема: Числовые последовательности
Общий
член числовой последовательности
![]() имеет
вид …
имеет
вид …
|
|
|
|
Тема: Числовые последовательности
Числовая последовательность задана формулой общего члена . Тогда значение равно …
|
|
|
|
Тема: Числовые последовательности
Числовая
последовательность задана рекуррентным
соотношением
![]() ,
,
![]() ,
,
![]() .
Тогда значение выражения
.
Тогда значение выражения
![]() равно
…
равно
…
|
|
|
12 |
Тема: Числовые последовательности
Общий член числовой последовательности имеет вид …
|
|
|
|
Тема: Числовые последовательности
Из числовых последовательностей , , , бесконечно малой не является последовательность …
|
|
|
|
Тема: Числовые последовательности
Из
числовых последовательностей
 ,
,
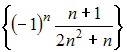 ,
,
 ,
,
 не
является
сходящейся последовательность …
не
является
сходящейся последовательность …
|
|
|
|
Тема: Числовые последовательности
Общий член числовой последовательности имеет вид …
|
|
|
|
Тема: Числовые последовательности
Числовая
последовательность задана формулой
общего члена
![]() .
Тогда значение
.
Тогда значение
![]() равно
…
равно
…
|
|
|
|
Тема: Числовые последовательности
Числовая
последовательность задана рекуррентным
соотношением
![]() ,
,
![]() ,
.
Тогда
,
.
Тогда
![]() равно
…
равно
…
|
|
|
|
Тема: Числовые последовательности
Предел
числовой последовательности
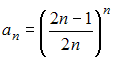 равен
…
равен
…
|
|
|
|
Тема: Числовые последовательности
Предел числовой последовательности равен …
|
|
|
|
Тема: Числовые последовательности
Общий член числовой последовательности имеет вид …
|
|
|
|
Тема: Числовые последовательности
Из числовых последовательностей , , , не является сходящейся последовательность …
|
|
|
|
Тема: Числовые последовательности
Предел числовой последовательности равен …
|
|
|
2 |
Тема: Числовые последовательности
Общий член числовой последовательности имеет вид …
|
|
|
|
Тема: Числовые последовательности
Из числовых последовательностей , , , бесконечно малой не является последовательность …
|
|
|
|
Тема: Сходимость числовых рядов
Даны
числовые ряды:
А)
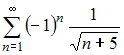 ,
В)
,
В)
 .
Тогда
…
.
Тогда
…
|
|
|
ряд А) сходится условно, ряд В) сходится абсолютно |
Тема: Сходимость числовых рядов
Сумма
числового ряда
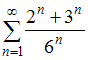 равна
…
равна
…
|
|
|
|
Тема: Сходимость числовых рядов
Даны
числовые ряды:
А)
 ,
В)
,
В)
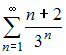 .
Тогда
…
.
Тогда
…
|
|
|
ряд А) расходится, ряд В) сходится |
Тема: Сходимость числовых рядов
Числовой
ряд
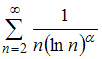 сходится
при
,
равном …
сходится
при
,
равном …
|
|
|
2 |
Тема: Сходимость числовых рядов
Даны
числовые ряды:
А)
 ,
В)
,
В)
 .
Тогда
…
.
Тогда
…
|
|
|
ряд А) сходится, ряд В) расходится |
Тема: Сходимость числовых рядов
Сумма
числового ряда
 равна
…
равна
…
|
|
|
|
Тема: Сходимость числовых рядов
Даны
числовые ряды:
А)
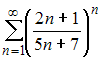 .
В)
.
В)
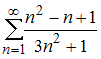 ,
Тогда
…
,
Тогда
…
|
|
|
ряд А) сходится, ряд В) расходится |
Тема: Сходимость числовых рядов
Сумма
числового ряда
 равна
…
равна
…
|
|
|
|
Тема: Сходимость числовых рядов
Сумма
числового ряда
 равна
…
равна
…
|
|
|
|
Тема: Сходимость числовых рядов
Даны числовые ряды: А) , В) . Тогда …
|
|
|
ряд А) сходится условно, ряд В) сходится абсолютно |
Тема: Сходимость числовых рядов
Сумма числового ряда равна …
|
|
|
|
Тема: Сходимость числовых рядов
Сумма числового ряда равна …
|
|
|
|
Тема: Сходимость числовых рядов
Даны числовые ряды: А) . В) , Тогда …
|
|
|
ряд А) сходится, ряд В) расходится |
Тема: Сходимость числовых рядов
Даны числовые ряды: А) , В) . Тогда …
|
|
|
ряд А) сходится, ряд В) расходится |
Тема: Сходимость числовых рядов
Числовой ряд сходится при , равном …
|
|
|
2 |
Тема: Сходимость числовых рядов
Даны
числовые ряды:
А)
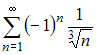 ,
В)
,
В)
 .
Тогда
…
.
Тогда
…
|
|
|
ряд А) сходится, ряд В) расходится |
Тема: Сходимость числовых рядов
Даны числовые ряды: А) . В) , Тогда …
|
|
|
ряд А) сходится, ряд В) расходится |
Тема: Сходимость числовых рядов
Даны числовые ряды: А) , В) . Тогда …
|
|
|
ряд А) сходится, ряд В) расходится |
Тема: Сходимость числовых рядов
Сумма числового ряда равна …
|
|
|
|
Тема: Сходимость числовых рядов
Даны числовые ряды: А) . В) , Тогда …
|
|
|
ряд А) сходится, ряд В) расходится |
Тема: Сходимость числовых рядов
Числовой ряд сходится при , равном …
|
|
|
2 |
Тема: Сходимость числовых рядов
Даны числовые ряды: А) , В) . Тогда …
|
|
|
ряд А) сходится, ряд В) расходится |
Тема: Сходимость числовых рядов
Сумма числового ряда равна …
|
|
|
|
Тема: Сходимость числовых рядов
Даны числовые ряды: А) , В) . Тогда …
|
|
|
ряд А) сходится условно, ряд В) сходится абсолютно |
Тема: Сходимость числовых рядов
Даны числовые ряды: А) , В) . Тогда …
|
|
|
ряд А) сходится, ряд В) расходится |
Тема: Сходимость числовых рядов
Даны числовые ряды: А) , В) . Тогда …
|
|
|
ряд А) сходится условно, ряд В) сходится абсолютно |
Тема: Область сходимости степенного ряда
Интервал
сходимости степенного ряда
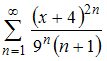 имеет
вид …
имеет
вид …
|
|
|
|
Тема: Область сходимости степенного ряда
Радиус
сходимости степенного ряда
 равен
…
равен
…
|
|
|
|
Тема: Область сходимости степенного ряда
Область
сходимости степенного ряда
 имеет
вид …
имеет
вид …
|
|
|
|
Тема: Область сходимости степенного ряда
Радиус
сходимости степенного ряда
 равен
5. Тогда интервал сходимости этого ряда
имеет вид …
равен
5. Тогда интервал сходимости этого ряда
имеет вид …
|
|
|
|
Тема: Область сходимости степенного ряда
Радиус
сходимости степенного ряда
 равен
…
равен
…
|
|
|
|
Тема: Область сходимости степенного ряда
Интервал
сходимости степенного ряда
 имеет
вид …
имеет
вид …
|
|
|
|
Тема: Область сходимости степенного ряда
Область
сходимости степенного ряда
 имеет
вид …
имеет
вид …
|
|
|
|
Тема: Область сходимости степенного ряда
Для
степенного ряда
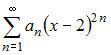 вычислен
предел
вычислен
предел
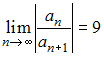 .
Тогда интервал сходимости данного ряда
имеет вид …
.
Тогда интервал сходимости данного ряда
имеет вид …
|
|
|
|
Тема: Область сходимости степенного ряда
Радиус
сходимости степенного ряда
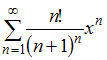 равен
…
равен
…
|
|
|
|
Тема: Область сходимости степенного ряда
Радиус
сходимости степенного ряда
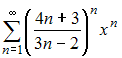 равен
…
равен
…
|
|
|
|
Дифференциальные уравнения
1.Типы дифференциальных уравнений
1.1.
Уравнение
![]() является
…
является
…
|
|
|
уравнением с разделяющимися переменными |
1.2.
Уравнение
![]() является
…
является
…
|
|
|
дифференциальным уравнением первого порядка в полных дифференциалах |
1.3.
Уравнение
![]() является
…
является
…
|
|
|
дифференциальным уравнением первого порядка в полных дифференциалах |
1.4.
Уравнение
![]() является
…
является
…
|
|
|
линейным неоднородным дифференциальным уравнением первого порядка |
1.5.
Уравнение
![]() является
…
является
…
|
|
|
уравнением в полных дифференциалах |
1.6.
Уравнение
![]() является
…
является
…
|
|
|
уравнением Бернулли |
1.7.
Уравнение
![]() является
…
является
…
|
|
|
линейным неоднородным дифференциальным уравнением первого порядка |
1.8.
Уравнение
 является
…
является
…
|
|
|
однородным
относительно
|
1.9.
Уравнение
![]() является
…
является
…
|
|
|
уравнением с разделяющимися переменными |
1.10.
Уравнение
![]() является
…
является
…
|
|
|
однородным относительно и дифференциальным уравнением первого порядка |
2.Однородные дифференциальные уравнения
2.1.
Дифференциальное
уравнение
![]() будет
однородным дифференциальным уравнением
первого порядка при
,
равном …
будет
однородным дифференциальным уравнением
первого порядка при
,
равном …
|
|
|
0 |
2.2.
Общий интеграл дифференциального
уравнения
![]() имеет
вид …
имеет
вид …
|
|
|
|
2.3.
Общий интеграл дифференциального
уравнения
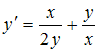 имеет
вид …
имеет
вид …
|
|
|
|
2.4.
Общее решение дифференциального
уравнения
![]() имеет
вид …
имеет
вид …
|
|
|
|
2.5.
Дифференциальное
уравнение
![]() будет
однородным дифференциальным уравнением
первого порядка при
будет
однородным дифференциальным уравнением
первого порядка при
![]() ,
равном …
,
равном …
|
|
|
3 |
2.6.
Дифференциальное
уравнение
![]() заменой
заменой
![]() приводится
к уравнению с разделенными переменными,
которое имеет вид …
приводится
к уравнению с разделенными переменными,
которое имеет вид …
|
|
|
|
2.7.
Общий
интеграл дифференциального уравнения
![]() имеет
вид …
имеет
вид …
|
|
|
|
2.8.
Дифференциальное
уравнение
![]() заменой
приводится
к уравнению с разделенными переменными,
которое имеет вид …
заменой
приводится
к уравнению с разделенными переменными,
которое имеет вид …
|
|
|
|
2.9.
Общее
решение дифференциального уравнения
![]() имеет
вид …
имеет
вид …
|
|
|
|
2.10.
Дифференциальное
уравнение
![]() будет
однородным дифференциальным уравнением
первого порядка при
,
равном …
будет
однородным дифференциальным уравнением
первого порядка при
,
равном …
|
|
|
4 |
3.Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами
3.1.
Общее решение линейного однородного
дифференциального уравнения второго
порядка
![]() имеет
вид …
имеет
вид …
|
|
|
|
3.2.
Общий вид частного решения
![]() линейного
неоднородного дифференциального
уравнения второго порядка
линейного
неоднородного дифференциального
уравнения второго порядка
![]() будет
выглядеть как …
будет
выглядеть как …
|
|
|
|
3.3.
Общий вид частного решения
![]() линейного
неоднородного дифференциального
уравнения второго порядка
линейного
неоднородного дифференциального
уравнения второго порядка
![]() будет
выглядеть как …
будет
выглядеть как …
|
|
|
|
3.4.
Общее решение линейного однородного
дифференциального уравнения второго
порядка
![]() имеет
вид …
имеет
вид …
|
|
|
|
3.5.
Общий
вид частного решения
линейного
неоднородного дифференциального
уравнения второго порядка
![]() будет
выглядеть как …
будет
выглядеть как …
|
|
|
|
3.6.
Общий
вид частного решения
линейного
неоднородного дифференциального
уравнения второго порядка
![]() будет
выглядеть как …
будет
выглядеть как …
|
|
|
|
3.7. Общий вид частного решения линейного неоднородного дифференциального уравнения второго порядка будет выглядеть как …
|
|
|
|
3.8.
Общее
решение линейного неоднородного
дифференциального уравнения второго
порядка
![]() имеет
вид …
имеет
вид …
|
|
|
|
3.9.
Частное
решение
линейного
неоднородного дифференциального
уравнения второго порядка
![]() имеет
вид …
имеет
вид …
|
|
|
|
3.10.
Общее
решение линейного однородного
дифференциального уравнения второго
порядка
![]() имеет
вид …
имеет
вид …
|
|
|
|
4.Системы двух линейных дифференциальных уравнений с постоянными коэффициентами
4.1.
Решение задачи Коши
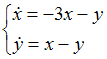 ,
,
![]() ,
имеет вид …
,
имеет вид …
|
|
|
|
4.2.
Общее решение системы дифференциальных
уравнений
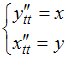 имеет
вид …
имеет
вид …
|
|
|
|
4.3.
Общее решение системы дифференциальных
уравнений
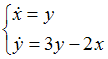 имеет
вид …
имеет
вид …
|
|
|
|
4.4.
При решении системы дифференциальных
уравнений
 можно
получить уравнение второго порядка
вида …
можно
получить уравнение второго порядка
вида …
|
|
|
|
4.5.
Общее
решение системы дифференциальных
уравнений
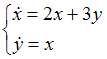 имеет
вид …
имеет
вид …
|
|
|
|
4.6. Общий вид частного решения линейного неоднородного дифференциального уравнения второго порядка будет выглядеть как …
|
|
|
|
4.7.
Решение
задачи Коши
 ,
,
![]() ,
имеет вид …
,
имеет вид …
|
|
|
|
4.8.
Решение
задачи Коши

![]() ,
имеет вид …
,
имеет вид …
|
|
|
|
4.9.
Решение
задачи Коши

![]() ,
имеет вид …
,
имеет вид …
|
|
|
|
4.10.
Общее
решение системы дифференциальных
уравнений
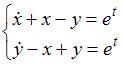 имеет
вид …
имеет
вид …
|
|
|
|