
- •3 Замена переменной в неопределенном интеграле
- •4Интегрирование по частям
- •5Определение интеграла и его свойства
- •Свойства интеграла
- •8Интегрирование рациональных дробей
- •6. Геометрические приложения определенного интеграла
- •9Интегрирование простейших дробей.
- •Интегрирование простейших дробей первого типа
- •10 Интегрирование иррациональных функций.
- •15 17Дифференциальные уравнения 1. Основные понятия
- •2. Линейные дифференциальные уравнения первого порядка
- •16Уравнения с разделяющимися переменными
- •18Дифференциальные уравнения, допускающие понижение порядка.
- •[Править]Охлаждение тела
1Свойства
первообразной и неопределенного
интеграла.Определение
первообразной.
Первообразной
функции f(x) на
промежутке (a;
b) называется
такая функция F(x),
что выполняется равенство ![]() для
любого х из
заданного промежутка.
Если принять
во внимание тот факт, что производная
от константы С равна
нулю, то справедливо равенство
для
любого х из
заданного промежутка.
Если принять
во внимание тот факт, что производная
от константы С равна
нулю, то справедливо равенство ![]() .
Таким образом, функция f(x) имеет
множество первообразных F(x)+C,
для произвольной константы С,
причем эти первообразные отличаются
друг от друга на произвольную постоянную
величину.
Определение
неопределенного интеграла.
Все
множество первообразных функции f(x) называется
неопределенным интегралом этой функции
и обозначается
.
Таким образом, функция f(x) имеет
множество первообразных F(x)+C,
для произвольной константы С,
причем эти первообразные отличаются
друг от друга на произвольную постоянную
величину.
Определение
неопределенного интеграла.
Все
множество первообразных функции f(x) называется
неопределенным интегралом этой функции
и обозначается ![]() .
Выражение
.
Выражение ![]() называют подынтегральным
выражением,
а f(x) – подынтегральной
функцией.
Подынтегральное выражение представляет
собой дифференциал функции f(x).
Действие
нахождения неизвестной функции по
заданному ее дифференциалу
называетсянеопределенным интегрированием,
потому что результатом интегрирования
является не одна функцияF(x),
а множество ее первообразных F(x)+C.
На
основании свойств производной можно
сформулировать и доказать свойства
неопределенного интеграла (свойства
первообразной).
называют подынтегральным
выражением,
а f(x) – подынтегральной
функцией.
Подынтегральное выражение представляет
собой дифференциал функции f(x).
Действие
нахождения неизвестной функции по
заданному ее дифференциалу
называетсянеопределенным интегрированием,
потому что результатом интегрирования
является не одна функцияF(x),
а множество ее первообразных F(x)+C.
На
основании свойств производной можно
сформулировать и доказать свойства
неопределенного интеграла (свойства
первообразной).
 Производная
результата интегрирования равна
подынтегральной функции.
Производная
результата интегрирования равна
подынтегральной функции.
 Неопределенный
интеграл дифференциала функции равен
сумме самой функции и произвольной
константы.
Неопределенный
интеграл дифференциала функции равен
сумме самой функции и произвольной
константы.
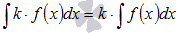 ,
где k –
произвольная константа.
Коэффициент
можно выносить за знак неопределенного
интеграла.
,
где k –
произвольная константа.
Коэффициент
можно выносить за знак неопределенного
интеграла.
 Неопределенный
интеграл суммы/разности функций равен
сумме/разности неопределенных интегралов
функций.
Неопределенный
интеграл суммы/разности функций равен
сумме/разности неопределенных интегралов
функций.
Промежуточные
равенства первого и второго свойств
неопределенного интеграла приведены
для пояснения.
Для доказательства
третьего и четвертого свойств достаточно
найти производные от правых частей
равенств:
 Эти
производные равны подынтегральным
функциям, что и является доказательством
в силу первого свойства. Оно же используется
в последних переходах.
Таким
образом, задача интегрирования является
обратной задаче дифференцирования,
причем между этими задачами очень тесная
связь:
Эти
производные равны подынтегральным
функциям, что и является доказательством
в силу первого свойства. Оно же используется
в последних переходах.
Таким
образом, задача интегрирования является
обратной задаче дифференцирования,
причем между этими задачами очень тесная
связь:
первое свойство позволяет проводить проверку интегрирования. Чтобы проверить правильность выполненного интегрирования достаточно вычислить производную полученного результата. Если полученная в результате дифференцирования функция окажется равной подынтегральной функции, то это будет означать, что интегрирование проведено верно;
второе свойство неопределенного интеграла позволяет по известному дифференциалу функции найти ее первообразную. На этом свойстве основано непосредственное вычисление неопределенных интегралов.
Рассмотрим
пример.
Пример.
Найти
первообразную функции ![]() ,
значение которой равно единице при х
= 1.
Решение.
Мы
знаем из дифференциального исчисления,
что
,
значение которой равно единице при х
= 1.
Решение.
Мы
знаем из дифференциального исчисления,
что ![]() (достаточно
заглянуть в таблицу производных основных
элементарных функций). Таким образом,
(достаточно
заглянуть в таблицу производных основных
элементарных функций). Таким образом, ![]() .
По второму свойству
.
По второму свойству ![]() .
То есть, имеем множество первообразных
.
То есть, имеем множество первообразных ![]() .
При х
= 1 получим
значение
.
При х
= 1 получим
значение ![]() .
По условию, это значение должно быть
равно единице, следовательно, С
= 1.
Искомая первообразная примет
вид
.
По условию, это значение должно быть
равно единице, следовательно, С
= 1.
Искомая первообразная примет
вид ![]() .
Пример.
Найти
неопределенный интеграл
.
Пример.
Найти
неопределенный интеграл ![]() и
результат проверить
дифференцированием.
Решение.
По
формуле синуса двойного угла из
тригонометрии
и
результат проверить
дифференцированием.
Решение.
По
формуле синуса двойного угла из
тригонометрии ![]() ,
поэтому
,
поэтому
![]() Из
таблицы производных для тригонометрических
функций имеем
Из
таблицы производных для тригонометрических
функций имеем
![]() То
есть,
То
есть, ![]() По
третьему свойству неопределенного
интеграла можем записать
По
третьему свойству неопределенного
интеграла можем записать ![]() Обращаясь
ко второму свойству,
получим
Обращаясь
ко второму свойству,
получим ![]() .
Следовательно,
.
Следовательно, ![]() Проверка.
Для
проверки результата продифференцируем
полученное выражение:
Проверка.
Для
проверки результата продифференцируем
полученное выражение:
![]() В
итоге получили подынтегральную функцию,
значит, интегрирование выполнено
правильно. В последнем переходе была
использована формула синуса двойного
угла.
Если таблицу производных
основных элементарных функций переписать
в виде дифференциалов, то из нее по
второму свойству неопределенного
интеграла можно составить таблицу
первообразных.
В
итоге получили подынтегральную функцию,
значит, интегрирование выполнено
правильно. В последнем переходе была
использована формула синуса двойного
угла.
Если таблицу производных
основных элементарных функций переписать
в виде дифференциалов, то из нее по
второму свойству неопределенного
интеграла можно составить таблицу
первообразных.
3 Замена переменной в неопределенном интеграле
Замена
переменной в неопределенном интеграле
производится с помощью подстановок
двух видов:
а) ![]() ,
где
,
где ![]() –
монотонная, непрерывно дифференцируемая
функция новой переменной t. Формула
замены переменной в этом случае:
–
монотонная, непрерывно дифференцируемая
функция новой переменной t. Формула
замены переменной в этом случае: ![]() ;
б)
;
б) ![]() ,
где U –
новая переменная. Формула замены
переменной при такой
подстановке:
,
где U –
новая переменная. Формула замены
переменной при такой
подстановке: ![]() .
Примеры.
1. Найти интеграл
.
Примеры.
1. Найти интеграл ![]() .
Решение. Перепишем данный интеграл в
виде
.
Решение. Перепишем данный интеграл в
виде ![]() .
Так как производная выражения
.
Так как производная выражения ![]() равна
2/х,
а второй множитель 1/х отличается
от этой производной только постоянным
коэффициентом 2, то нужно применить
подстановку
равна
2/х,
а второй множитель 1/х отличается
от этой производной только постоянным
коэффициентом 2, то нужно применить
подстановку ![]() .
Тогда
.
Тогда ![]() .
Следовательно,
.
Следовательно,
![]() .
2. Найти интеграл
.
2. Найти интеграл ![]() .
Решение.
.
Решение. ![]() ,
тогда
,
тогда ![]() и
и
![]() .
.
4Интегрирование по частям
Нахождение
интеграла ![]() по
формуле
по
формуле ![]() называется
интегрированием по частям. ЗдесьU=U(х),υ=υ( x)
непрерывно дифференцируемые функции
от х.
С помощью этой формулы нахождение
интеграла сводится к отысканию другого
интеграла
называется
интегрированием по частям. ЗдесьU=U(х),υ=υ( x)
непрерывно дифференцируемые функции
от х.
С помощью этой формулы нахождение
интеграла сводится к отысканию другого
интеграла ![]() ,
ее применение целесообразно в тех
случаях, когда последний интеграл либо
проще исходного, либо ему подобен.
При этом за υ берется такая функция,
которая при дифференцировании упрощается,
а за dU –
та часть подынтегрального выражения,
интеграл от которой известен или может
быть найден.
Так например,
для интегралов вида
,
ее применение целесообразно в тех
случаях, когда последний интеграл либо
проще исходного, либо ему подобен.
При этом за υ берется такая функция,
которая при дифференцировании упрощается,
а за dU –
та часть подынтегрального выражения,
интеграл от которой известен или может
быть найден.
Так например,
для интегралов вида ![]() ,
, ![]() ,
, ![]() ,
где P(x)
– многочлен, за υ следует принятьP(x),
а за dU соответствует
выражение
,
где P(x)
– многочлен, за υ следует принятьP(x),
а за dU соответствует
выражение ![]() ,
, ![]() .
Для интегралов вида
.
Для интегралов вида ![]() за
υ принимаются соответственно функции
за
υ принимаются соответственно функции ![]() ,
а за
,
а за ![]() –
выражение P(x)dx.
Пример.
Найти интеграл
–
выражение P(x)dx.
Пример.
Найти интеграл ![]() .
Решение. Положим
.
Решение. Положим ![]() ,
тогда
,
тогда ![]() .
Отсюда
.
Отсюда ![]()
5Определение интеграла и его свойства
Определение. Пусть ![]() .
Пусть
.
Пусть ![]() ,
, ![]() аддитивна,
и ее плотность равна
аддитивна,
и ее плотность равна ![]() .
Тогда
называется
интегралом.
.
Тогда
называется
интегралом.
Обозначение. Пусть ![]() .
Значение функции
на
отрезке
.
Значение функции
на
отрезке ![]() :
:
![]()
Теорема
(Ньютон, Лейбниц). Пусть
, ![]() –
первообразная функции
.
Тогда
–
первообразная функции
.
Тогда ![]()
![]()
Доказательство. По
теореме о плотности аддитивной функции
промежутка, ![]() и
равна плотности функции
и
равна плотности функции ![]() .
По определению тогда
–
интеграл функции
.
.
По определению тогда
–
интеграл функции
.
![]()
Свойства интеграла
1. ![]()
![]()
2. ![]() .
.
Доказательство. Пусть
- первообразная
, ![]() –
первообразная
–
первообразная ![]() .
Тогда
.
Тогда ![]() –
первообразная
–
первообразная ![]() .
.
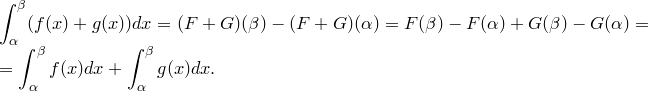
3. ![]() .
.
4. Пусть
функция ![]() ,
дифференцируема.
Пусть функция
задана
на промежутке, содержащем множество
значений функции
,
дифференцируема.
Пусть функция
задана
на промежутке, содержащем множество
значений функции
![]() ,
причем
,
причем ![]() .
Пусть у функции
есть
первообразная. Тогда
.
Пусть у функции
есть
первообразная. Тогда
![]()
Доказательство. Пусть – первообразная функции . Тогда

Следствие. Пусть ![]() .
Тогда
.
Тогда
![]()
Доказательство. Положим ![]() ,
применим предыдущую теорему:
,
применим предыдущую теорему:
![]()
5. Пусть ![]() ,
функции
и
дифференцируемы,
функция
,
функции
и
дифференцируемы,
функция ![]() имеет
первообразную. Тогда
имеет
первообразную. Тогда
![]()
Доказательство.
![]()
Функции ![]() и
имеют
первообразные, поэтому и функция
и
имеют
первообразные, поэтому и функция ![]() также
имеет первообразную, и можем записать
также
имеет первообразную, и можем записать

Определение. Пусть
, ![]() ,
, ![]() .
Тогда
.
Тогда
![]()
Задача
1. Пусть ![]() .
Докажите, что
.
Докажите, что
7
Производная интеграла с переменным верхним пределом |
Если
в определенном интеграле Обозначим
верхний предел x,
а переменную интегрирования, чтобы
не смешивать ее с верхним пределом,
обозначим t.
Таким образом, интеграл с переменным
верхним пределом является функцией
от x: Имеет
место теорема: производная
интеграла с переменным верхним пределом
от непрерывной функции равна
подынтегральной функции, в которой
переменная интегрирования заменена
верхним пределом: Доказательство. По определению производной
Тогда Это
значит, что интеграл с переменным
верхним пределом |

 изменять
верхний предел b,
то будет меняться и значение интеграла,
то есть интеграл будет функцией
верхнего предела.
изменять
верхний предел b,
то будет меняться и значение интеграла,
то есть интеграл будет функцией
верхнего предела. .
.
 где
где  [первый
интеграл представим в виде суммы двух
интегралов, пользуясь свойством
аддитивности]=
[первый
интеграл представим в виде суммы двух
интегралов, пользуясь свойством
аддитивности]=