Уравнение неразрывности

Ниже приведены примеры уравнений непрерывности, которые выражают одинаковую идею непрерывного изменения некоторой величины. Уравнения непрерывности — (сильная) локальная формазаконов сохранения.В электродинамике уравнение непрерывности выводится из уравнений Максвелла. Оно утверждает,чтодивергенция плотности тока равна изменению плотности заряда со знаком минус,ВыводЗакон Ампера гласитВзяв дивергенцию от обоих частей выражения, получим но дивергенция ротора равняется нулю, таким образом По теореме Гаусса Подставляя это выражение в предыдущее уравнение, получаем искомое уравнение непрерывности.Теория волнВ теории волн уравнение непрерывности выражает собой закон сохранения энергии в элементарном объеме, в котором распространяются волны любой природы. Его дифференциальная форма где   — вектор плотности потока энергии в точке с координатами   в момент времени  ,  — плотность энергии.ВыводПо определению, вектор плотности потока энергии — это вектор, модуль которого равен энергии, переносимой через единичную площадку, перпендикулярную направлению переноса энергии, за единицу времени, т.е.  , а направление его совпадает с направлением переноса энергии. Тогда энергия, вытекающая в единицу времени из некоторого макроскопического объема V, По закону сохранения энергии  , где W_in — энергия, находящаяся в объеме V. По определению, плотность энергии — энегрия единицы объема, тогда полная энегрия, заключенная в данном объеме, равна тогда выражение для потока энергии примет вид Применяя формулу Гаусса-Остроградского к левой части выражения, получим В силу произвольности выбранного объема, заключаем что подынтегральные выражения равны, откуда и получаем дифференциальную форму уравнения непрерывности.Гидродинамика.В гидродинамике уравнение непрерывности, иногда называемое уравнением неразрывности, выражает собой закон сохранения массы в элементарном объеме, то есть непрерывность потока жидкости или газа. Его дифференциальная форма где   — плотность жидкости (или газа),   — вектор скорости жидкости (или газа) в точке с координатами   в момент времени  .Вектор   называют плотностью потока жидкости. Его направление совпадает с направлением течения жидкости, а абсолютная величина определяет количество вещества, протекающего в единицу времени через единицу площади, расположенную перпендикулярно вектору скорости.Для несжимаемых жидкостей  . Поэтому уравнение принимает вид ,из чего следует соленоидальность поля скорости.Квантовая механикаВ нерелятивистской квантовой механике сохранение вероятности также приводит к уравнению непрерывности. Пусть P(x, t) — плотность вероятности, тогда уравнение запишется в виде где j — ток вероятности.

Уравнение Бернулли для элементарной струйки

2.4

где z – геометрическая высота, т.е. расстояние от произвольной горизонтальной плоскости сравнения до рассматриваемой точки в сечении (рис. 2.4). Индексы относятся к номерам сечений, проведенным нормально линиям тока;

p/γ – пьезометрическая высота, соответствующая полному или манометрическому давлению;

u²/(2g) – скоростной напор (высота) или удельная кинетическая энергия.

Удельная кинетическая энергия – кинетическая энергия единицы веса (массы) движущейся жидкости. Уравнение (2.4) называется уравнением Бернулли для элементарной струйки и является частной формой закона сохранения энергии.

Элементарная струйка – семейство (пучок) линий тока, проходящих через все точки бесконечно малой площадки.

Линия тока – линия, в каждой точке которой в данный момент времени вектор скорости направлен по касательной к ней.В этом виде оно обычно применяется к элементарной струйке невязкой жидкости при отмеченных выше условиях движения и доказывает постоянство суммы z + p/γ + u²/(2g)для всех ее живых сечений вдоль течения. Индексы 1 и 2 относятся к двум произвольно выбранным сечениям 1-1 и 2-2 (см. рис. 2.4).

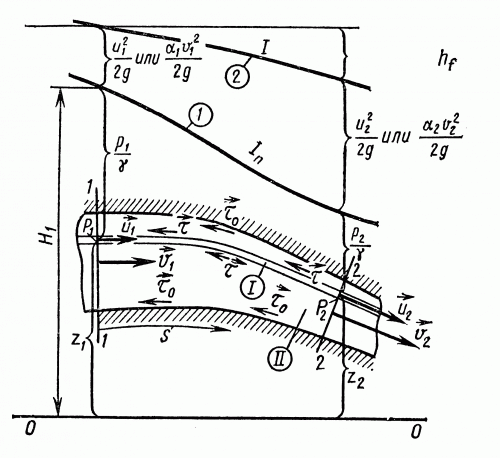
Рис. 2.4. Уравнение Бернулли для элементарной струйкиВсе эти отрезки, отложенные последовательно по вертикали, образуют в сумме величину H₀ = z + p/γ+u²/(2g),называемую гидродинамическим(полным)напором.Линия 1 на рис. 2.4, характеризующая изменение вдоль течения пьезометрического напора,называется пьезометрической линией.Ее уклон, т.е. изменение пьезометрического напора вдоль пути перемещения жидкости I_п, называется пьезометрическим уклоном. Уравнение Бернулли - основное уравнение гидравликиДля двух сечений потока 1—1 и 2—2 реальной жидкости (рисунок 1) при установившемся плавно изменяющемся движении уравнение Бернулли имеет вид:z₁ + p₁/γ + α₁υ₁²/(2g) = z₂ + p₂/γ + α₂υ₂²/(2g) + Σh_п    (1)где z — ордината, определяющая высоту положения центра выбранного сечения над произвольной горизонтальной плоскостью сравнения 0—0; p/γ — пьезометрическая высота;z + p/γ = H_п — гидростатический напор; αυ²/(2g) = h_v — скоростная высота, или скоростной напор; α — коэффициент Кориолиса, учитывающий неравномерность распределения скоростей в живом сечении потока.Сумма трех членов:z + p/γ + αυ²/(2g) = H есть полный напор; Σh_п — потеря напора между выбранными сечениями потока. Вместо выражения (1) можно написать:H₁ = H₂ + Σh_п.Все члены уравнения Бернулли в формуле (1) имеют линейную размерность и в энергетическом смысле представляют удельную энергию жидкости, т. е. энергию, отнесенную к единице веса жидкости.Так, z и p/γ - удельная потенциальная энергия соответственно положения и давления;  z + p/γ - удельная потенциальная энергия жидкости;  αυ²/(2g) - удельная кинетическая энергия, выраженная через среднюю скорость потока в данном сечении. Сумма всех трех членов z + p/γ + αυ²/(2g) = H представляет полный запас удельной механической энергии жидкости в данном сечении потока;  Σh_п - удельная механическая энергия, затрачиваемая на преодоление сопротивления движению жидкости между сечениями потока и переходящая в тепловую энергию, которая состоит из следующих слагаемых:Σh_п = Σh_дл + Σh_местгде Σh_дл — потери энергии (напора) на трение по длине; Σh_мест — местные потери энергии (напора).Если уравнение (1) умножить на γ, то получим:γz₁ + p₁ + γα₁υ₁²/(2g) = γz₂ + p₂ + γα₂υ₂²/(2g) + γΣh_п     (2).Члены уравнения (2) имеют размерность давления и представляют энергию, отнесенную к единице объема.Если уравнение (1) умножить на g, то получимgz₁ + p₁/ρ + α₁υ₁²/2 = gz₂ + p₂/ρ + α₂υ₂²/2 + gΣh_п     (3)Члены уравнения (3) имеют размерность м²/с² и представляют энергию, отнесенную к единице массы.

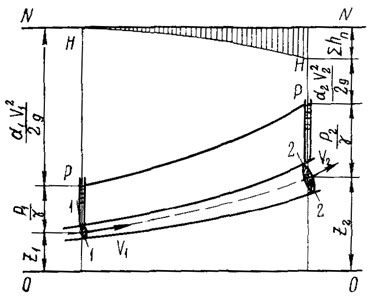На рисунке 1 приведена диаграмма уравнения Бернулли для потока реальной жидкости. Здесь 0—0 — плоскость сравнения; N—N — плоскость начального напора; Н—Н — напорная линия, или линия полной удельной энергии. Падение ее на единицу длины представляет гидравлический уклон J; Р—Р — пьезометрическая линия, или линия удельной потенциальной энергии. Падение ее на единицу длины представляет пьезометрический уклон J_п.Так как общий запас удельной энергии вдоль потока непрерывно уменьшается, линия Н—Н всегда нисходящая, а гидравлический уклон всегда положительный (J>0). Пьезометрическая линия может быть и нисходящей, и восходящей (последнее имеет место на расширяющихся участках, когда средняя скорость потока уменьшается), поэтому пьезометрический уклон может быть и положительным (J>0), и отрицательным(J<0).На участках с равномерным движением жидкости, где имеют место только потери напора на трение по длине, линии Н—Н и Р—Р представляют взаимно параллельные прямые, поэтому J = J_п =h_дл/L. 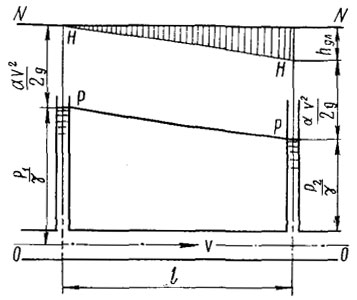В этом случае потеря напора может быть определена по разности гидростатических напоров:h_дл = (z₁ + p₁/γ) - (z₂ + p₂/γ)Для горизонтальных участков потоков (z₁=z₂) или в случае, если плоскость сравнения 0—0 проведена по оси потока (z₁=z₂=0) (рисунок 2), потеря напора на трение по длине может быть определена непосредственно по разности показаний пьезометров:h_дл = (p₁ — p₂)/γНа рисунке 3 показаны линия энергии Н—Н и пьезометрическая линия P—P для трубопровода переменного сечения, соединяющего два открытых резервуара.