
- •1.Электрические заряды и их свойства.
- •2. Сила и плотность постоянного электрического тока.
- •3.Циркуляция вектора намагниченности.
- •1.Закон Кулона.
- •2.Уравнение непрерывности.
- •3.Напряженность магнитного поля. Циркуляция вектора н.
- •1.Электрическое поле. Напряженность поля.
- •2.Закон Ома для однородного проводника в интегральной и локальной форме. Следствия.
- •3.Связь между вектором намагниченности и н, а также между в и н.
- •1.Потенциал.
- •3.Условия на границе двух магнетиков.
- •1.Связь между напряженностью и потенциалом поля.
- •2.Закон Ома в интегральной форме для неоднородного участка цепи.
- •3.Закон электромагнитной индукции. Правило Ленца.
- •1.Поток вектора е. Теорема Гаусса в интегральной форме.
- •2.Правила Кирхгофа.
- •3.Природа эл.Магн. Индукции (контур движется в магнитном поле).
- •1.Дифференциальная форма теоремы Гаусса для вектора е.
- •2.Мощность постоянного тока.
- •3.Природа эл.Магн. Индукции (контур покоится в переменном магнитном поле).
- •1.Электрический диполь.
- •2.Закон Джоуля – Ленца.
- •3.Самоиндукция.
- •1.Сила, действующая на диполь во внешнем электрическом поле.
- •2.Взаимодействие проводников с током.
- •3.Взаимная индукция.
- •1.Момент сил, действующих на диполь, энергия диполя в поле.
- •1) Под действием результирующей силы он перемещается в область более сильного поля,
- •2) Момент сил стремится установить диполь так, чтобы .
- •3.Классификация магнетиков.
- •1.Поляризация диэлектриков.
- •2.Магнитное поле движущегося заряда.
- •3.Энергия магнитного поля.
- •1.Объемные и связанные заряды диэлектрика.
- •2.Закон Био – Савара.
- •3.Магнитные свойства атомов. Магнитомеханическое отношение.
- •1.Электрическое поле в диэлектрике.
- •2.Сила Лоренца.
- •3.Опыт Эйнштейна и де – Хааса.
- •1.Поляризованность. Связь между р и е.
- •2.Закон Ампера.
- •3.Собственный механический и магнитный моменты электрона. Магнетон Бора.
- •1.Теорема Гаусса для вектора р.
- •2.Сила и момент сил, действующие на контур с током в однородном магнитном поле.
- •3.Диамагнетизм.
- •1.Вектор электрического смещения. Теорема Гаусса для вектора d. Линии вектора d.
- •2.Сила и момент сил, действующие на контур с током в неоднородном магнитном поле.
- •3.Магнитные моменты атомов.
- •1.Теорема о циркуляции вектора е. Потенциальное поле.
- •2.Теорема Гаусса для вектора в.
- •3.Парамагнетизм.
- •1.Условия для электростатического поля на границе двух диэлектриков.
- •2.Теорема о циркуляции вектора в.
- •1.Проводник во внешнем электрическом поле.
- •2.Импульс и плотность импульса эл.Магн. Поля.
- •3.Вихревое электрическое поле.
- •1.Поле у поверхности проводника.
- •2.Циркуляция и ротор электростатического поля.
- •3.Ток смещения. Теорема о циркуляции вектора н.
- •2. (Дивергенция и ротор электростатического поля). Давление эл.Магн. Волны
- •3.Система уравнений Максвелла в интегральной форме.
- •1.Энергия заряженного проводника.
- •2.Намагничение вещества. Вектор намагниченности.
- •3.Система уравнений Максвелла в дифференциальной форме.
- •1.Энергия заряженного конденсатора.
- •3.Электромагнитная волна.
- •Циркуляция вектора намагниченности.
- •1.Энергия и плотность энергии электростатического поля.
- •2.Циркуляция вектора намагниченности.
- •3.Энергия эл.Магн. Волны. Вектор Пойнтинга.
- •1.Энергия взаимодействия электрических зарядов.
- •2.Напряженность магнитного поля. Циркуляция вектора н.
- •3.Система уравнений Максвелла.
3.Условия на границе двух магнетиков.
На границе магнетиков векторы и должны удовлетворять определенным граничным условиям, которые следуют из выполнения теоремы Гаусса и теоремы о циркуляции для этих векторов:
![]() ;
;
Поместим очень
малой высоты цилиндрик на границе двух
магнетиков. Рис.7.6. Поток вектора
наружу из этого цилиндрика без учета
через боковую поверхность равен:
![]() .
Проекция
.
Проекция
![]() записывается со знаком “минус”,
т.к. нормаль к нижнему основанию цилиндра
направлена наружу, а вектор
записывается со знаком “минус”,
т.к. нормаль к нижнему основанию цилиндра
направлена наружу, а вектор![]() направлен к основанию. Таким образом,
граничное условие для нормальных
составляющих вектора
имеет вид:
направлен к основанию. Таким образом,
граничное условие для нормальных
составляющих вектора
имеет вид:
![]() ,
т.е. они равны по обе стороны границы.
,
т.е. они равны по обе стороны границы.
![]()
 Для
нормальных составляющих вектора
граничное
условие найдем из соотношения
Для
нормальных составляющих вектора
граничное
условие найдем из соотношения
![]() с
учетом условия
,
тогда:
с
учетом условия
,
тогда:
![]()

![]()
Рис.7.6.
Рис.7.7.
Теперь возьмем на
границе малый прямоугольный контур, в
пределах которого векторы
и
не изменяются и вычислим для него
циркуляцию вектора
.
Учтем, что вдоль поверхности может
протекать поверхностный ток проводимости
с линейной плотностью
![]() .
Тогда, считая, что высота контура мала,
запишем проекции на ось x,
направленную влево:
.
Тогда, считая, что высота контура мала,
запишем проекции на ось x,
направленную влево:
![]() ,
,
![]() -
проекция вектора
на нормаль
-
проекция вектора
на нормаль
![]() к контуру. Нормаль образует с направлением
обхода контура правовинтовую систему.
Если ток проводимости на границе есть,
то тангенциальные составляющие
претерпевают скачок:
к контуру. Нормаль образует с направлением
обхода контура правовинтовую систему.
Если ток проводимости на границе есть,
то тангенциальные составляющие
претерпевают скачок:
![]()
Если на поверхности раздела токов нет, то они равны:
![]()
Для тангенциальных
составляющих вектора
найдем соотношение, записывая отношение
тангенциальных составляющих
![]() через
через
![]() .
Тогда:
.
Тогда:
![]()
Таким образом,
если на границе раздела двух однородных
магнетиков тока проводимости нет, то
при переходе этой границы составляющие
![]() и
и
![]() изменяются
непрерывно, без скачка. Составляющие
изменяются
непрерывно, без скачка. Составляющие
![]() и
и
![]() претерпевают скачок. Вектор
ведет себя аналогично вектору смещения
в электростатике, а вектор
-
аналогично вектору
.
претерпевают скачок. Вектор
ведет себя аналогично вектору смещения
в электростатике, а вектор
-
аналогично вектору
.
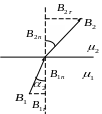 Линии
вектора
преломляются, при этом отношение
тангенсов углов, рис.7.8:
Линии
вектора
преломляются, при этом отношение
тангенсов углов, рис.7.8:

Рис.7.8. Рис.7.9.

, что при отсутствии токов проводимости дает:
![]() .
.
На рис.7.9 изображено
магнитное поле для векторов
и
вблизи границы двух магнетиков при
отсутствии токов проводимости для
![]() .
При сравнении густоты линий видно, что
.
При сравнении густоты линий видно, что
![]() ,
а
,
а
![]() .
Линии вектора
не терпят разрыва на границе, а линии
терпят
разрыв из-за поверхностных токов
намагничивания
.
.
Линии вектора
не терпят разрыва на границе, а линии
терпят
разрыв из-за поверхностных токов
намагничивания
.
На преломлении магнитных линий основано действие магнитной защиты и магнитных линз. При внесении, например, замкнутой железной оболочки (слоя) во внешнее магнитное поле линии поля будут концентрироваться (сгущаться) преимущественно в самой оболочке. Внутри же оболочки, в ее полости, магнитное поле оказывается сильно ослабленным по сравнению с внешним полем. Т.е. железная оболочка обладает экранирующим действием, что используется для защиты чувствительных к магнитным полям приборов.
Б-5
Связь между напряженностью и потенциалом поля.
Закон Ома в интегральной форме для неоднородного участка цепи.
Закон электромагнитной индукции. Правило Ленца.
