2.Теорема о циркуляции вектора в.

З апишем выражение для циркуляции вектора для магнитного поля постоянных токов в вакууме . Вычислим этот интеграл для магнитного поля прямого тока. Пусть плоскость замкнутого контура перпендикулярна току, рис.6.9. Ток перпендикулярен плоскости чертежа и направлен за чертеж.

I

I

Рис.6.9а Рис.6.9б

В каждой точке контура вектор направлен по касательной к окружности, проведенной через эту точку. Запишем выражение для циркуляции как ,где - проекция элемента длины контура на направление вектора . Из рис. видно, что , тогда = = . Интегрируя по углу: . При обходе по контуру (по часовой стрелке) радиальная прямая все время поворачивается в одном направлении и . Значит,

Если ток не охватывается контуром, рис.6.9б, то при обходе по контуру радиальная прямая поворачивается сначала в одном направлении (участок 1-2), а потом – в противоположном, (участок 2-1), вследствие чего , значит, если контур не охватывает ток, циркуляция вектора равна нулю. Знак выражения зависит от направления обхода по контуру, в этом же направлении отсчитывается и угол . Если направление тока образует с направлением обхода правовинтовую систему, эта величина положительная и, наоборот.

С помощью этой формулы легко вспомнить индукцию поля прямого тока, рис.6.10. Циркуляция в этом случае равна , откуда

, эта формула справедлива и для провода произвольной формы, например, для кругового тока.

Если токи текут через поверхность, охватываемую контуром, то ток представляют через плотность. тока:

Интеграл берется по произвольной поверхности , натянутой на контур, есть плотность тока в той точке, где расположена площадка , - положительная нормаль к ней. Значит, теорему Гаусса можно записать в виде:

.

3.Ферромагнетизм.

Особый класс магнетиков представляют ферромагнетики, обладающие намагниченностью в отсутствие внешнего магнитного поля. Кроме железа к ним относятся кобальт, никель, гадолиний, их сплавы и соединения, а также сплавы и соединения марганца и хрома с неферромагнитными материалами. Ферромагнетизм проявляется только в кристаллическом состоянии вещества.

Намагниченность ферромагнетика в 10¹⁰ раз больше диа- и парамагнетика, которые являются слабомагнитными веществами.

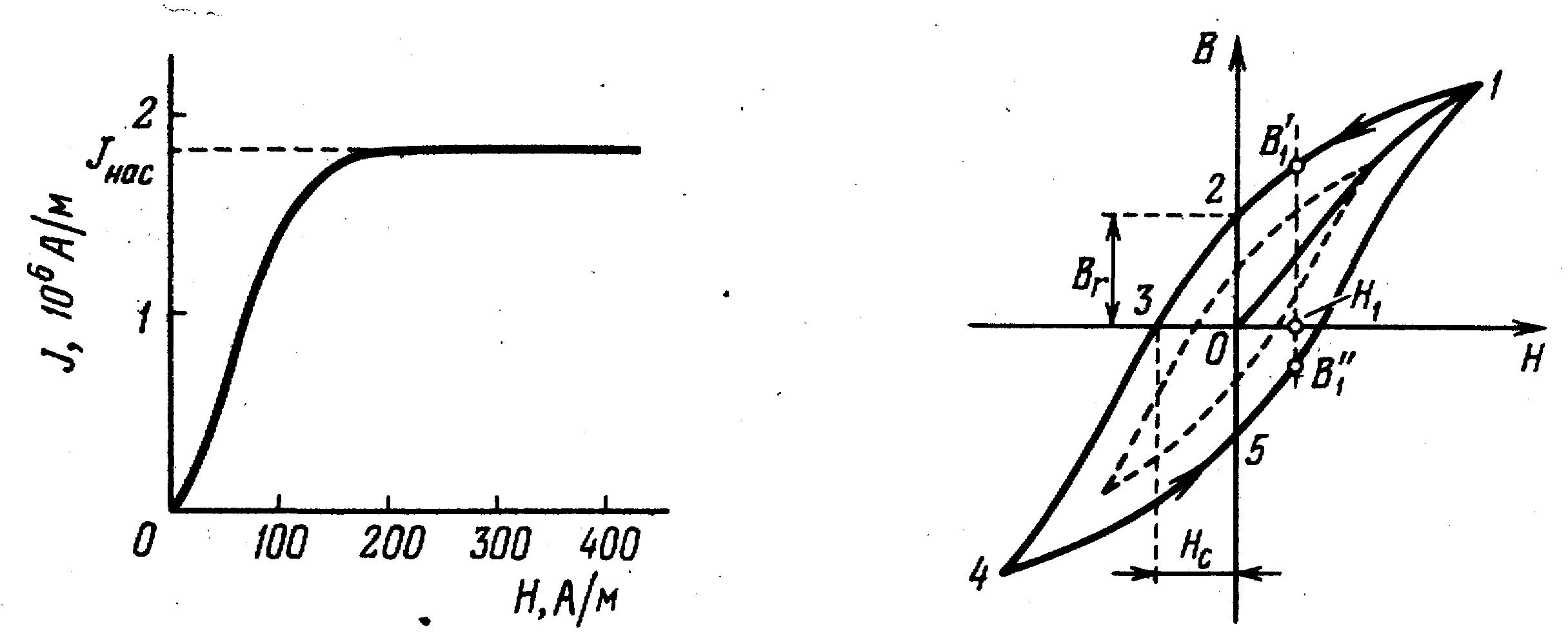
Рис.8.5а Рис.8.5б

Если в слабомагнитных веществах намагниченность линейно зависит от напряженности магнитного поля  , то для ферромагнетиков она более сложная. На рис.8.5а дана кривая намагничения ферромагнетика, магнитный момент которого вначале был равен нулю. Она называется основной кривой намагничения. Уже в полях порядка 100 A/м намагниченность достигает насыщения.

Кроме нелинейной зависимости от для ферромагнетика характерно явление гистерезиса. Если довести намагничение до насыщения (точка 1), а затем уменьшать внешнее поле , то индукция следует не по кривой 0-1, а по кривой 1-2. И при =0 намагничение не исчезает, а характеризуется - остаточной индукцией. Чтобы намагниченность исчезла, необходимо приложить внешнее поле в противоположном направлении, рис.8.5б.

Явление остаточной намагниченности позволяет изготавливать постоянные магниты.

При действии на ферромагнетик переменного магнитного поля индукция меняется по кривой 1-2-3-4-5-1, называемой петлей гистерезиса, рис.8.5б. Гистерезис приводит к тому, что намагниченность не является однозначной функцией поля, а зависит от предыстории образца, поэтому понятие магнитная проницаемость применяется к основной кривой намагничения.

Основы теории ферромагнетизма были созданы Френкелем и Гейзенбергом в 1928 г. Из опытов следует, что магнитные свойства ферромагнетиков обусловлены собственными (спиновыми) магнитными моментами электронов. При определенных условиях в кристаллах возникают силы (обменного взаимодействия), которые заставляют магнитные моменты электронов выстраиваться параллельно друг другу. Возникают области (домены) спонтанного намагничения до насыщения с размерами 1-10 мкм и с различными направлениями магнитных моментов.

При включении внешнего поля происходит смещение границ доменов, их ориентация, что приводит к резкому возрастанию магнитного момента магнетика. Эти процессы являются необратимыми, что объясняет явления гистерезиса.

Для каждого ферромагнетика имеется температура, называемая точкой Кюри Т_с, при которой домены распадаются и ферромагнетик становится парамагнетиком. Для железа Т_с = 768С, для никеля - 365С. Для такого парамагнетика выполняется закон Кюри – Вейсса:

.

В некоторых случаях (хром, марганец, и др.) обменные силы приводят к возникновению антиферромагнетизма. Это явление было предсказано Ландау в 1933г.

Б19

1. Проводник во внешнем электрическом поле.

2. Импульс и плотность импульса эл.магн. поля.

3. Вихревое электрическое поле.