4. Фреймы

Фрейм – это абстрактный образ для представления некого стереотипа восприятия.

Фрейм – формализованная модель для отображения образа.

Различают фреймы-образцы, хранящиеся в базе знаний, и фреймы–экземпляры, которые создаются для отображения реальных фактических ситуаций на основе поступающих данных.

Все многообразие знаний о мире можно отобразить через:

1. фреймы-структуры – для обозначения объектов и понятий (заем, залог, вексель);

2. фреймы-роли (менеджер, кассир, клиент);

3. фреймы-сценарии (банкротство, собрание акционеров);

4. фреймы-ситуации (тревога, авария, рабочий режим устройства).

Любой фрейм содержит набор атрибутов – слотов, значениями которых являются конкретные данные. Каждый слот имеет уникальное имя.

Пример фрейма «Лекция»

ПРЕДМЕТ	Информатика
ЛЕКТОР	Красилов И.И.
АУДИТОРИЯ	403
СЛУШАТЕЛИ	97

Фрейм может содержать процедуры, которые будут выполняться при определенных условиях.

Существует несколько способов получения слотом значений во фрейме-экземпляре:

• по умолчанию от фрейма-образца;

• через наследование свойств от фрейма, указанного в слоте АКО (A-Kind-Оf, это);

• по формуле, указанной в слоте;

• через присоединенную процедуру;

• явно из диалога с пользователем;

• из базы данных.

В качестве значения слота может выступать имя другого фрейма. Тогда образуются сети фреймов.

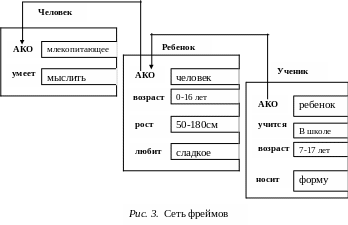
Преимущества: 1) отражает концептуальную основу организации памяти человека, а также ее гибкость и наглядность; 2) однородность представления знаний и возможность их типового текстового описания с помощью специальных языков представления знаний (н-р, FRL, KRL). Примеры фрейм-ориентированных экспертных системы – ANALYST, МОДИС, TRISTAN, ALTERID.

5. Формальные логические модели

Формальная логика – наука об общих структурах и законах правильного мышления, образования и сочетания понятий и высказываний, о правилах умозаключений независимо от их конкретного содержания.

Моделирование логики рассуждений происходит по схеме: из одной или нескольких посылок (которые считаются истинными) следует сделать «логически верное заключение» (вывод, следствие). И посылки, и заключение должны быть представлены на понятном языке, адекватно отображающем предметную область, в которой проводится вывод. В обычной жизни это наш естественный язык общения; в математике это язык определенных формул.

Логические выражения, построенные в данном языке, могут быть истинными или ложными. Некоторые из этих выражений, являющиеся всегда истинными, объявляются аксиомами (или постулатами). Они составляют ту базовую систему посылок, исходя из которой и пользуясь определенными правилами вывода, можно получить заключения в виде новых выражений, также являющихся истинными.

Классическими примерами аксиоматических (формальных) систем являются исчисление высказываний и исчисление предикатов.

Исчисление высказываний – область математической логики, называемая булевой алгеброй. Она изучает высказывания и операции над ними. Высказывание – это предложение, которое может быть истинно или ложно. Наиболее известными операциями булевой алгебры являются конъюнкция и дизъюнкция.

Так, дизъюнкция высказываний – новое высказывание:

• сконструированное их двух и более исходных высказываний;

• истинное в тех случаях, когда истинно хотя бы одно из исходных высказываний.

Конъюнкция высказываний – новое высказывание:

• сконструированное из двух и более исходных высказываний;

• истинное в тех случаях, когда истинны все исходные высказывания.

В булевой алгебре высказывания рассматриваются как нераздельные целые и только с точки зрения их истинности или ложности. Ни структура высказываний, ни их содержание не затрагиваются.

В то же время и в науке, и в практике используются заключения, существенно зависящие как от структуры, так и от содержания используемых в них высказываний. Возникает необходимость в расширении логики высказываний – в логике предикатов.

Логика предикатов расчленяет элементарное высказывание на субъект (подлежащее) и предикат (сказуемое). Субъект – это то, о чем что-то утверждается в высказывании; предикат – это то, что утверждается о субъекте (н-р, в высказывании «7 – простое число», «7» – субъект, «простое число» – предикат). Это высказывание утверждает, что «7» обладает свойством «быть простым числом».

Если число 7 заменить переменной Х из множества натуральных чисел N, то получим высказывательную форму «Х – простое число». При одних значениях Х (н-р, Х=13, Х=17) она дает истинные высказывания, а при других значениях Х (н-р, Х=10, Х=18) – ложные высказывания.

Эта высказывательная форма определяет функцию одной переменной Х, определенной на множестве N, и принимающую значения из множества {1;0}. Здесь предикат становится функцией субъекта и выражает свойство субъекта.

Достоинство формальных систем – исчисления высказываний и исчисления предикатов – в том, что они хорошо исследованы и имеют прекрасно разработанные модели логического вывода.

Поэтому все, что может и гарантирует каждая из этих систем, гарантируется и для прикладных формальных систем как моделей конкретных предметных областей. В частности, это гарантии непротиворечивости вывода, алгоритмической разрешимости (для исчисления высказываний) и полуразрешимости (для исчислений предикатов).

Недостатки – закрытость, негибкость. Модификация и расширение всегда связаны с перестройкой всей формальной системы, что для практических систем сложно и трудоемко. Поэтому формальные системы как модели представления знаний могут использоваться только в тех предметных областях, которые хорошо локализуются и мало зависят от внешних факторов.

К тому же, очень высокие требования к предметной области – полнота и непротиворечивость «базового аксиоматического набора» – обусловили то, что в промышленных экспертных системах формальные логические модели практически не используются.