Оценка точности совместных измерений

Исходные данные:

1. Измерение электрического сопротивления R медного стержня при разной температуре дали следующие результаты:

Таблица 1 – Экспериментальные данные

i	1	2	3	4	5	6	7
ti , 0C	19,1	25,0	30,1	36,0	40,0	45,1	50,0
Ri , Ом	76,30	77,80	79,75	80,80	82,35	83,90	85,10

Провести обработку экспериментально полученных данных, представленных в таблице 1.

По данным таблицы 1 необходимо:

- установить математическую модель;

- обработать результаты измерений;

- построить график, указать на графике доверительный интервал (Р = 0,95)

Математическая модель объекта исследования– приближённое описание какого-либо класса явлений внешнего мира, выраженное с помощью математической символики. Математическая модель – мощный метод познания внешнего мира, а также прогнозирования и управления. Анализ математической модели позволяет проникнуть в сущность изучаемых явлений.

Процедуру получения математической модели объекта можно разбить на следующие этапы:

1. Составление гносеологической (мысленной) модели объекта. Исходя из технического задания и изучения режимов работы объекта, у инженера возникает приближенная мысленная модель, которая в дальнейшем уточняется и приобретает вид математической модели.

2. Определение независимых переменных, которые характеризуют объект, и уточнение их размерностей. При этом число управляющих воздействий не может быть меньше числа выходных переменных. Размерность переменных состояния не может быть меньше размерности выходных переменных. Размерность возмущающих воздействий M может быть произвольной и никак не связана с размерностью y, x, u.

3. Запись физических законов, в силу которых развиваются процессы в объекте.

4. Приведение уравнений объекта к стандартному, с точки зрения теории автоматического управления, виду.

Математическая модель никогда не бывает тождественна рассматриваемому объекту, так как при ее составлении всегда делают какие-либо допущения и упрощения. Поэтому для одной и той же системы, в зависимости от целей управления, она может быть разной.

При составлении математической модели приходится искать компромиссный вариант между двумя противоречивыми требованиями: с одной стороны, модель должна наиболее полно отражать свойства реальной системы; с другой стороны - она должна быть простой, чтобы не затруднять исследований.

Задача построения математической модели в данной работе сводится к тому, чтобы выявить зависимость измеряемого сопротивления от температуры.

Анализируя исходные данные, получаем следующую математическую модель:

Полученная зависимость является нелинейной.

Измеренными величинами являются - и .

Искомые величины - , и .

Где, и - температурные коэффициенты электрического сопротивления;

- сопротивление проводника при температуре 20 ⁰С, Ом.

Обработка результатов совместных измерений

Совместные измерения — проводимые одновременно измерения двух или нескольких неодноимённых величин для определения зависимости между ними.

В практике измерений встречаются случаи, когда искомые величины не могут быть измерены непосредственно и представлены как явные функции непосредственно измеряемых величин. В таких случаях измеряют величины функционально связанные с искомыми величинами.

Обработка экспериментальных данных методом наименьших квадратов

В общем виде уравнение для трех неизвестных величин можно представить как:

,

где искомые величины;

непосредственно измеряемые величины.

Для данной задачи уравнение имеет вид:

,

где искомые величины;

непосредственно измеряемые величины.

Решение данного уравнения проводится по способу наименьших квадратов. Для того чтобы применить способ наименьших квадратов необходимо выполнить ряд требований, одним из которых является – нормальность распределения. Но так как (по задаче число измерений равно 7), то проверить гипотезу о виде распределения экспериментальных данных невозможно. Допускаем, что распределение экспериментальных данных является нормальным.

В соответствии с принципом Лежандра искомые величины имеют наиболее достоверное решение, если сумма квадратов функции независимых величин принимает наименьшее значение:

Условие выполняется, если полный дифференциал функции равен нулю:

Условие суммы полного дифференциала выполняется, если все частные производные также равны нулю:

Полученная система представляет собой систему нормальных уравнений, где число уравнений равно числу неизвестных.

Примем:

; .

Раскрывая скобки получим:

Составим матрицу коэффициентов:

Рассчитаем значения членов матрицы:

Подставим в матрицу полученные значения:

Определим дискриминант матрицы:

Заменим первый столбец матрицы на столбец свободных членов, найдем дискриминант полученной матрицы :

= 23260366967,2729

Заменим второй столбец матрицы на столбец свободных членов, найдем дискриминант полученной матрицы :

87358596,2112

Заменим третий столбец матрицы на столбец свободных членов, найдем дискриминант полученной матрицы :

6972,0669

Рассчитаем оценки искомых величин , и используя следующие формулы:

Полученные оценки подставляем в условные уравнения:

Вычисляем остаточные погрешности:

СКО условных уравнений (остаточных погрешностей) вычисляют по формуле:

,

где число условных уравнений:

число искомых величин:

Отсюда получаем:

Среднее квадратическое отклонение вычисленных значений искомых величин определяют по формулам:

; ;

алгебраические дополнения элементов определителя матрицы, получаемые путем удаления из исходной матрицы столбца и строчки, на пересечении которых находится данный элемент:

Алгебраическое дополнение получаем, вычеркивая первую строку и первый столбец исходной матрицы, тогда:

Алгебраическое дополнение получаем, вычеркивая вторую строку и второй столбец исходной матрицы, тогда:

Алгебраическое дополнение получаем, вычеркивая третью строку и третий столбец исходной матрицы, тогда:

Тогда среднее квадратическое отклонение искомых величин будет равно:

2.2 Построение доверительного интервала

Определив СКО полученных оценок искомых величин строим доверительный интервал для истинного значения величины, используя распределение Стьюдента. Число степеней свободы при этом для всех измеряемых величин равно: Тогда:

при

Доверительный интервал погрешности результата измерений - интервал значений случайной погрешности, внутри которого с заданной вероятностью находится искомое значение погрешности результата измерений.

Для значения доверительный интервал имеет вид:

Истинное значение находится в интервале:

Для значения доверительный интервал имеет вид:

Истинное значение находится в интервале:

Для значения доверительный интервал имеет вид:

Истинное значение находится в интервале:

Заключительным этапом обработки результатов совместных измерений является построение графика функции .

Составим таблицу данных для построения графика функции:

Таблица 2 – Исходные данные для построения графика

t
20,0	76,526	75,947	77,105
25,0	77,962	76,858	79,065
30,1	79,427	77,638	81,217
36,0	81,124	78,349	83,899
40,0	82,275	78,715	85,835
45,1	83,744	79,046	88,442
50,0	85,157	79,221	91,093

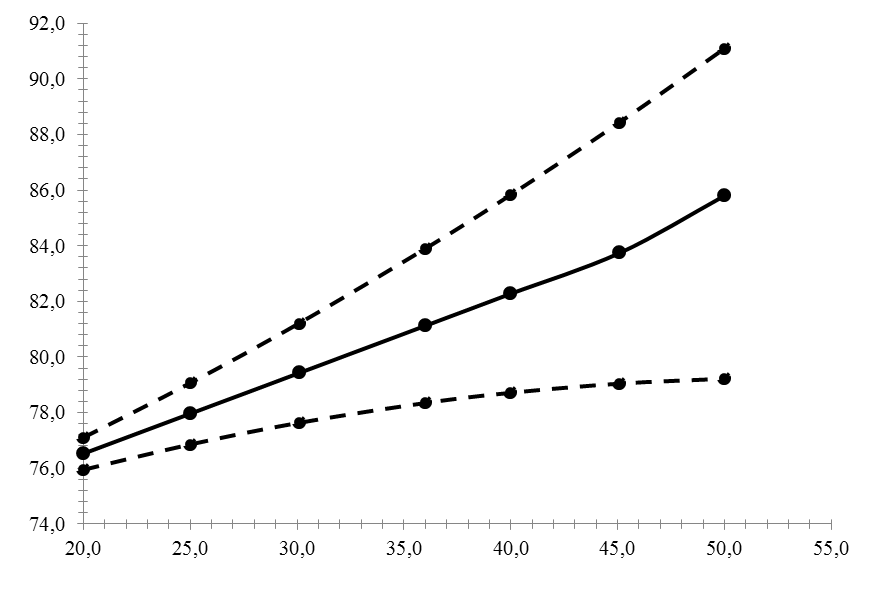
Рисунок 1 - График зависимости сопротивления от температуры

Анализируя график функции можно сказать о том, что погрешность определения искомых величин лежит в доверительном интервале, обозначенном на рисунке 1. Также можно судить о том, что с увеличением температуры увеличивается погрешность измерения сопротивления.