
- •Информационно измерительные системы.
- •Введение.
- •2.1. Дискретизация сигналов.
- •2.2. Методы дискретизации. Дискретизация посредством выборок.
- •2.2.1. Равномерная дискретизация. Теорема Котельникова.
- •2.2.2. Свойства функций отсчетов.
- •2.2.3. Первое следствие теоремы Котельникова.
- •2.2.4. Второе следствие теоремы Котельникова.
- •2.2.5. Теорема Котельникова для сигналов, имеющих ограниченный спектр (полосовой спектр, помещающийся в полосе определенных частот).
- •3. Аналого-цифровое преобразование.
- •3.1. Оцифровка.
- •3.2. Квантование по уровню (выборка-хранение).
- •1 Способ.
- •2 Способ.
- •3.3. Квантование сигналов при наличии помех.
- •4. Теоретические основы передачи дискретной информации в иис.
- •4.1. Основные понятия.
- •4.2. Пропускная способность каналов связи и теоремы оптимального кодирования.
- •4.2.1. Пропускная способность дискретного канала без помех.
- •4.2.2. Теорема Шеннона для дискретного канала без помех.
- •4.2.3. Скорость передачи информации и пропускная способность дискретного канала с помехами.
- •4.2.4. Основная теорема Шеннона для дискретного канала с помехами.
- •4.3. Отношение сигнал/шум и скорость передачи информации по каналу связи с помехами.
- •4.4. Влияние распределения шумов по спектру (форма кривой спектральной плотности) на скорость передачи информации.
- •5. Согласование сенсоров с каналами передачи информации.
- •5.1. Методы уплотнения каналов.
- •5.1.1. Уплотнение (селекция) по времени.
- •5.1.2. Частотное уплотнение (селекция).
- •5.2.5. Определение энтропии комплексного датчика.
- •5.2.6. Определение скорости опроса комплексного датчика.
- •5.2.7. Согласование скорости выдачи информации комплексного датчика с пропускной способностью канала.
- •5.2.8. Зависимость комплексного датчика от отношения сигнал/шум.
2.2.5. Теорема Котельникова для сигналов, имеющих ограниченный спектр (полосовой спектр, помещающийся в полосе определенных частот).
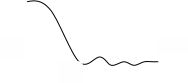
Рис 5

Рис 6
Радиосигналы (промодулирована низкочастотными колебаниями)

Рис 7
Спектр высокочастотный, т.к. график начинается не из 0.
Если
задана функция времени
спектром в полосе частот
 ,
где
,
где
 (высокочастотная), то она представима
своими отсчетами, взятыми через интервал
(высокочастотная), то она представима
своими отсчетами, взятыми через интервал
 .
При этом в каждой точке отсчета необходимо
подсчитать значения и амплитуды, и фазы
сигнала.
.
При этом в каждой точке отсчета необходимо
подсчитать значения и амплитуды, и фазы
сигнала.
Если
 то количество отсчетов
то количество отсчетов
 .
.
Поскольку
мы берем отсчеты амплитуды и фазы, то
количество отсчетов равно
 .
.
Таким образом, непрерывная функция , имеющая спектр в полосе , представляется с помощью такого же количества отсчетов, что и произвольная функция из теоремы Котельникова.
Доказательство этого утверждения аналогично уже проведенного нами для сигнала, имеющего полосу от 0 до .
Результатом такого доказательства будет Ряд Котельникова для высокочастотного сигнала.

где
 – значение амплитуды огибающей
высокочастотного сигнала в k-той
точке отсчета,
– значение амплитуды огибающей
высокочастотного сигнала в k-той
точке отсчета,
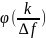 – значение
фазы высокочастотного сигнала в k-той
точке отсчета,
– значение
фазы высокочастотного сигнала в k-той
точке отсчета,
 -
среднее значение круговой частоты,
определяемое граничными значениями
спектра сигнала:
-
среднее значение круговой частоты,
определяемое граничными значениями
спектра сигнала:

Для
определения отсчетных значений
и
целесообразно представить значение
амплитуды и фазы в виде непрерывных
функций времени
и
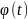 ,
а затем производить дискретные отсчеты
через промежутки времени
,
а затем производить дискретные отсчеты
через промежутки времени
 .
.
Формула 1:

Где синус – огибающая, а косинус – несущая.

Рис 8
Амплитуда функции отсчета задается первым множителем, огибающей. Ее вид аналогичен виду функции отсчетов низкочастотного сигнала.
Множитель
 характеризует высокочастотный характер
функции отсчета и определяется средней
круговой частотой, фазой и смещен на
время
характеризует высокочастотный характер
функции отсчета и определяется средней
круговой частотой, фазой и смещен на
время
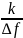 ,
т.е. в точку отсчета.
,
т.е. в точку отсчета.
Из
последнего рисунка видно, что ширина
основного лепестка функции отсчетов
одинакова для всех моментов отсчета и
равна
 .
.
Поскольку
любое колебание с полосой частот
 определяется суммой функции отсчетов
с шириной огибающей
,
следовательно, любая функция времени
с таким спектром будет иметь самые
короткие выбросы примерно такой же
длительности.
определяется суммой функции отсчетов
с шириной огибающей
,
следовательно, любая функция времени
с таким спектром будет иметь самые
короткие выбросы примерно такой же
длительности.
Так например, если - шумовое напряжение с полосой , то оно может иметь наиболее короткие выбросы с длительностью приблизительно равной .

Рис 9

Рис 10
3. Аналого-цифровое преобразование.
3.1. Оцифровка.
Итак, аналоговый сигнал необходимо преобразовать в поток двоичных слов, соответствующих моментом взятия выборок t.

Рис 11
Эти отсчеты (двоичные слова, соответствующие им) поступают на вход процессора параллельно, т.е. в виде одного полного слова на каждую выборку.
При оцифровке в последовательность чисел вносятся ошибки и искажения. Эти ошибки возникают по нескольким причинам:
-
есть погрешность взятия отсчетов

-
возникает амплитудная погрешность
 ,
погрешность, которая тем больше, чем
круче функция.
,
погрешность, которая тем больше, чем
круче функция.
В
действительности
 меняется в пределах полосы, ограниченной
_._._
меняется в пределах полосы, ограниченной
_._._


 определяется
следующими составляющими:
определяется
следующими составляющими:
- ошибка квантования;
- погрешность АЦП;
-
погрешность в задании точек
 (отбора выбора);
(отбора выбора);
- погрешность, возникающая при взятии выборки.
