
- •Интеллектуальные мехатронные системы
- •Лекция № 8. Синтез нечетких регуляторов
- •4.1. Практические примеры построения ису с нечеткими регуляторами
- •4.1.1. Нечеткий регулятор для управления неустойчивым объектом
- •Методы функций близости
- •Методы дискриминантных функций
- •Процедуры самообученя распознаванию образов
- •Статистические методы распознавания.
- •Лингвистические методы распознавания образов.
- •1.Синтез нечеткого регулятора электропривода постоянного тока в среде «MatLab» Синтез нечеткого регулятора с одним входом и выходом.
- •Основные компоненты нечеткого логического вывода. Фаззификатор.
- •Дефаззификатор.
- •Оптимизация нечеткого регулятора.
- •2.Синтез комплексного закона управления электроприводом постоянного тока с помощью нечеткой логики.
- •Настройка быстродействующего регулятора.
- •2.3. Настройка точного регулятора.
- •Повышение точности
- •Синтез комбинированного управления
1.Синтез нечеткого регулятора электропривода постоянного тока в среде «MatLab» Синтез нечеткого регулятора с одним входом и выходом.
Проблема состоит в том, чтобы заставить привод точно следить за различными входными сигналами. Выработка управляющего воздействия осуществляется нечетким регулятором, в котором структурно можно выделить следующие функциональные блоки: фаззификатор, блок правил и дефаззификатор.
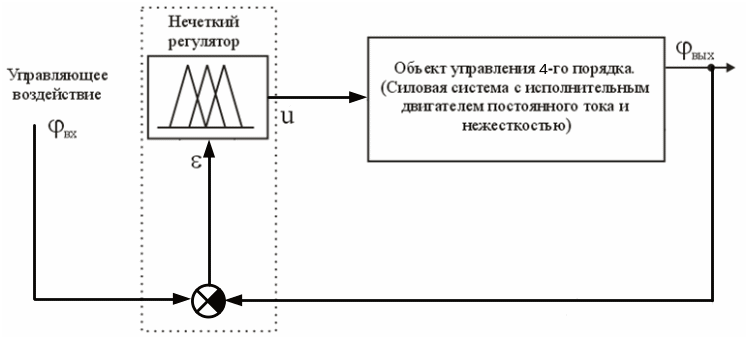 Рис.4
Обобщенная функциональная схема системы
с двумя лингвистическими переменными.
Рис.4
Обобщенная функциональная схема системы
с двумя лингвистическими переменными.
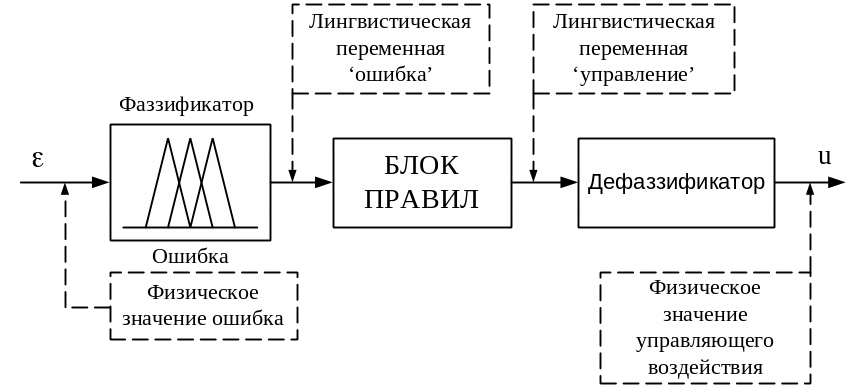 Рис.5
Принципиальная схема нечеткого регулятора
с двумя лингвистическими переменными.
Рис.5
Принципиальная схема нечеткого регулятора
с двумя лингвистическими переменными.
Алгоритм нечеткого управления в общем случае представляет собой преобразование входных переменных нечеткого регулятора в его выходные переменные с помощью следующих взаимосвязанных процедур:
1. преобразование входных физических переменных, получаемых от измерительных датчиков с объекта управления во входные лингвистические переменные нечеткого регулятора;
2. обработка логических высказываний, называемых лингвистическими правилами, относительно входных и выходных лингвистических переменных регулятора;
3. преобразование выходных лингвистических переменных нечеткого регулятора в физические управляющие переменные.
Рассмотрим сначала самый простой случай, когда для управления следящим электроприводом вводятся всего две лингвистические переменные:
«угол» - входная переменная;
«управляющее воздействие» - выходная переменная.
Синтез регулятора будем осуществлять в среде «MatLab» с помощью тулбокса «Fuzzy Logic». Он позволяет создавать системы нечеткого логического вывода и нечеткой классификации в рамках среды MatLab, с возможностью их интегрирования в Simulink. Базовым понятием Fuzzy Logic Toolbox является FIS-структура - система нечеткого вывода (Fuzzy Inference System). FIS-структура содержит все необходимые данные для реализации функционального отображения “входы-выходы” на основе нечеткого логического вывода согласно схеме, приведенной на рис. 6.
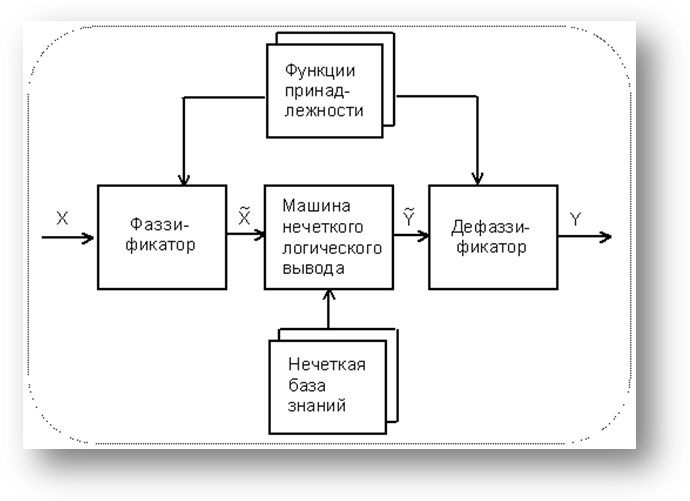 Рисунок 6.
Нечеткий логический вывод.
Рисунок 6.
Нечеткий логический вывод.
X -
входной четкий вектор;![]() -
вектор нечетких множеств, соответствующий
входному вектору X;
-
вектор нечетких множеств, соответствующий
входному вектору X;
![]() -
результат логического вывода в виде
вектора нечетких множеств;Y - выходной
четкий вектор.
-
результат логического вывода в виде
вектора нечетких множеств;Y - выходной
четкий вектор.
Модуль fuzzy позволяет строить нечеткие системы двух типов - Мамдани и Сугэно. В системах типа Мамдани база знаний состоит из правил вида “Если x1=низкий и x2=средний, то y=высокий”. В системах типа Сугэно база знаний состоит из правил вида “Если x1=низкий и x2=средний, то y=a0+a1x1+a2x2". Таким образом, основное отличие между системами Мамдани и Сугэно заключается в разных способах задания значений выходной переменной в правилах, образующих базу знаний. В системах типа Мамдани значения выходной переменной задаются нечеткими термами, в системах типа Сугэно - как линейная комбинация входных переменных. В нашем случаем будем использовать систему Сугэно, т.к. она лучше поддается оптимизации.
Для управления следящим электроприводом, вводятся две лингвистические переменные: «ошибка» (по положению) и «управляющее воздействие». Первая из них является входной, вторая – выходная. Определим терм-множество для указанный переменных.
