Министерство образования и науки Российской Федерации

Санкт-Петербургский государственный электротехнический

Университет «ЛЭТИ» им. В.И. Ульянова (Ленина)

Кафедра ТОЭ

Курсовая работа

по теме

«АНАЛИЗ ЛИНЕЙНОЙ ЦЕПИ»

Выполнила: *******

ФЭЛ

гр. ******

Преподаватель: Башарин С.А.

Санкт-Петербург

2008

Цепь задана тройками чисел:

141 – ИТ i₁; 224 –R_н= 1 Ом; 314 –R₃= 0,5 Ом; 434 –R₄= 0,5 Ом; 513 –L₅=1 Гн;

632 – L₆= 0,5 Гн.

На рис. 1 приведена схема данной цепи, для которой будет выполняться задание курсовой работы.

1. Анализ цепи операторным методом при воздействии одиночного импульса на входе.

Вмомент времениt=0 на вход цепи при нулевых независимых начальных условиях подается сигнал в виде одиночного импульса тока, форма которого приведена на рис. 2.

Параметры сигнала:

I_m= 10A;

t_и= 1,5 с.

t

0. Определение функции передачи цепи.

Функция передачи цепи по току определяется как , где I₁(S),I₂(S) – изображения по Лапласу реакции и воздействия.

Изображаем операторную схему цепи, в которой L-элементы заменяем операторными сопротивлениямиZ_L=SL(рис.1.1).

Z_H = R_H = 1;

Z₃ = R₃ = 0,5;

Z₄ = R₄ = 0,5;

Z₅ = Sּ1 = S;

Z₆ = Sּ0,5 = 0,5S.

Представим цепь в виде четырехполюсника, к левым зажимам которого подключается источник, а к правым – сопротивление нагрузки (рис.1.2).

Метод пропорциональных величин:

I₂(S) = 1;

U_H(S) = i₂(S)ּZ_H = 1;

U₆ = i₂ּZ₆ = 1ּ0.5S = 0.5S;

U₄ = U₆ + U_H;

U₄ = 0.5S + 1;

i₄ = S + 2;

i₅ = i₄ + i₆; i₅ = S + 2 + 1 = S + 3;

U₅ = i₅ּZ₅; U₅ = (S + 3)S = S² + 3S.

Для дальнейшего удобства расчета перерисуем цепь (рис. 1.3).

,,

, , ____

, , .

,

Передаточная функция:

Рассчитаем функцию передачи токов приS= 0,S­∞.

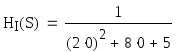
H_I(∞) = 0

Проверим полученные значения H_I(0) иH_I(∞) по схемам замещения, соответствующимS= 0 (рис. 1.4.а), гдеLКЗ, иS­∞ (рис. 1.4,б), гдеL­ХХ.

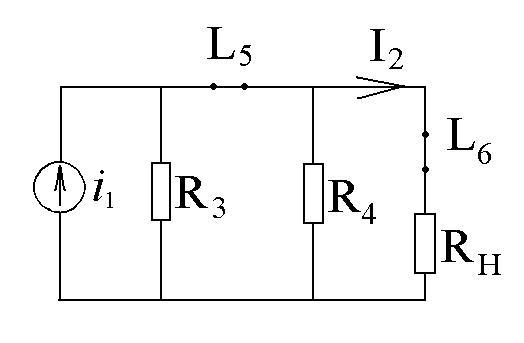
а б

рис. 1.4

Из схемы рис. 1.4, а:

U₃ = U₄ = U_H = U

Из схемы рис. 1.4, б:

I₂ = 0,

Проверка по схемам замещения для H_I(0) иH_I(∞) дала такие же результаты, какие были получены при расчете передаточной функции операторным методом. Таким образом, можно сделать вывод, что эти значения были найдены верно.

0. Определение нулей и полюсов функции передачи.

Нули – корни полинома числителя, полюса – корни полинома знаменателя передаточной функции цепи.

Конечных нулей не имеет. Найдем полюса:

S₁=−0.78

S₂=−3.22

Расположение полюсов на плоскости комплексной частоты приведено на рис. 1.5.

Исходя из вида полюсов (отрицательные, простые), можно заключить, что переходный процесс в рассматриваемой цепи имеет апериодический, затухающий характер. Его практическая длительность:

0. Определение переходной характеристики цепи.

Передаточную характеристику h₁(t) – реакцию цепи на единичную ступенчатую функцию δ₁(t) при нулевых независимых начальных условиях – находим как оригинал функции передачи цепи.

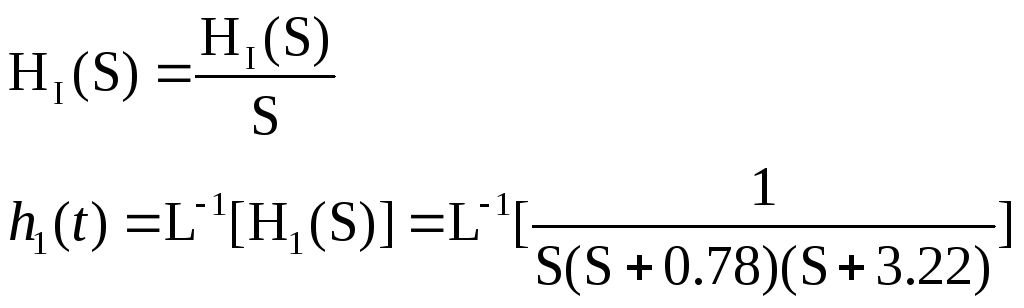
S₁ = 0,

S₂=−0.78,

S₃=−3.22.

Таким образом,

Определим значения h₁(t) приt= 0⁺и приt∞.

Проверим полученные значения по схемам замещения исходной цепи, соответствующим t=0⁺ (рис. 1.6, а), гдеLХХ, иt∞ (рис 1.6, б), гдеLКЗ.

а б

рис. 1.6

Из схемы рис. 1.6, а: h₁(0⁺) =I₂(0⁺) = 0.

Из схемы рис. 1.6, б по теореме о предельном значении функции:

Это сошлось с полученными выше значениями. Следовательно, вычисления выполнены верно.

График переходной характеристики цепи представлен на рис. 1.7.