
 ФЕДЕРАЛЬНОЕ
АГЕНТСТВО ПО ОБРАЗОВАНИЮ
ФЕДЕРАЛЬНОЕ
АГЕНТСТВО ПО ОБРАЗОВАНИЮ
Государственное образовательное учреждение высшего профессионального образования
«Санкт-Петербургский государственный электротехнический университет
"ЛЭТИ" имени В.И. Ульянова (Ленина)»

Кафедра МО ЭВМ
ИНДИВИДУАЛЬНОЕ ЗАДАНИЕ № 1
по дисциплине «Теория вычислительных процессов»
Часть 4 численная процедура минимизация булевской функции на гиперкубах
Вариант 13
Выполнил студент группы 4351 Довбыш А.А.
Руководитель Красюк В.И.

Санкт-Петербург
2007 г
Содержание
ИНДИВИДУАЛЬНОЕ ЗАДАНИЕ № 1 0
Выполнил студент группы 4351 Довбыш А.А. 0
Санкт-Петербург 1
1. Общие сведения 3
2. Численная процедура минимизация на гиперкубах 4
Список литературы 0
1. Общие сведения
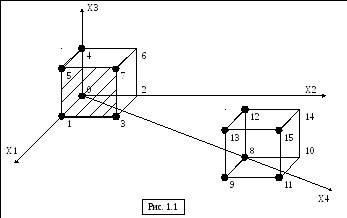
Определение:
Элементом гиперкуба будем называть множество из 2m (m = 0, 1, 2, .. , n – 1) вершин, обладающих (n – m) равными координатами (n – размерность гиперкуба, m – размерность элемента гиперкуба).
Различают следующие элементы гиперкуба:
m = 0, 20 = 1 – вершина (например, вершина 0 на рисунке 1.1);
m = 1, 21 = 1 – ребро (например, ребро 1-3 на рисунке 1.1);
m = 2, 22 = 1 – грань (например, грань 1-3-7-5 на рисунке 1.1);
n > m ≥ 3, 2m – подкуб размерности m.
Семейство элементов гиперкуба – покрытие множества его вершин.
Определение:
Элемент функции – элемент гиперкуба, такой, что все входящие в него вершины являются элементами множества Т.
Определение:
Основной элемент функции – элемент функции, который не является подмножеством ни одного другого элемента функции.
Каждому основному элементу функции соответствует простая импликанта этой функции.
Минимальной формой гиперкуба является приведенная система основных элементов функции:
1) | xl – xk | = 2i-1
2) | index xl – index xk | = 1
3) xk > xl index xk > index xl
Определение:
Опорная вершина гиперкуба – элемент функции размерности 0 (вершина), относительно которого мы будем искать другие элементы функции.
2. Численная процедура минимизация на гиперкубах
В качестве исходных данных мы имеем множество T = {0, 1, 3, 4, 5, 7, 8, 9, 11, 12, 13, 15, 16, 17, 19, 20, 21, 23, 24, 25, 26, 27, 28, 29, 31}. Нам необходимо найти минимальную форму функции на этом множестве с помощью численной процедуры минимизации на гиперкубах. Сначала построим гиперкуб для данного множества (см. рис. 2.1).
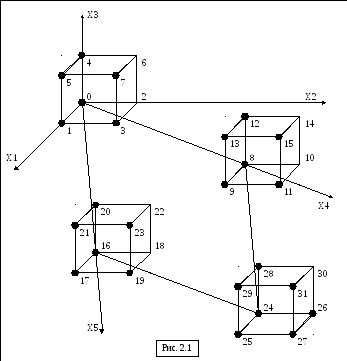
Элементы функции размерности 0 (вершины) выделены на рисунке 2.1 жирными точками. Они соответствуют исходному множеству Т.
Для определения элементов функции большей размерности выберем начальную опорную вершину (J* = 0) и найдем ее ближайших соседей:
J1=J* + (-1)0 20= 0 + 1 = 1
J2=J*
+
(-1)0
21=
0 + 2 = 2
J3=J* + (-1)0 22= 0 + 4 = 4
J4=J* + (-1)0 23= 0 + 8 = 8
J5=J* + (-1)0 24= 0 + 16 = 16
Таким образом, элементы размерности 1 для опорной вершины J*=0 будут следующими:
J1={0, 1}
J3={0, 4}
J4={0, 8}
J5={0, 16}
Необходимым условием для проверки наличия элементов размерности 2 является наличие более одного элемента размерности 1.
J13= J1+J3-J* = 1+4-0 = 5
J14= J1+J4-J* = 1+8-0 = 9
J15= J1+J5-J* = 1+16-0 = 17
J34= J3+J4-J* = 4+8-0 = 12
J35= J3+J5-J* = 4+16-0 = 20
J45= J4+J5-J* = 8+16-0 = 24
Найдем элементы размерности 2 для опорной вершины J*=0:
J13= (0, 1, 4, 5)
J14= (0, 1, 8, 9)
J15= (0, 1, 16, 17)
J34= (0, 4, 8, 12)
J35= (0, 4, 16, 20)
J45= (0, 8, 16, 24)
Необходимым условием для проверки наличия элементов размерности 3 является наличие не менее трех попарно смежных элемента размерности 2.
(J13, J14, J34) J134 = J1+J3+J4-2J* = 1+4+8-2*0 = 13
(J13, J15, J35) J135 = J1+J3+J5-2J* = 1+4+16-2*0 = 21
(J14, J15, J45) J145 = J1+J4+J5-2J* = 1+8+16-2*0 = 25
(J34, J35, J45) J345 = J3+J4+J5-2J* = 4+8+16-2*0 = 28
Тогда элементы размерности 3 для опорной вершины J*=0 будут следующими:
J134= {0, 1, 4, 5, 8, 9, 12, 13}
J135= {0, 1, 4, 5, 16 ,17, 20, 21}
J145= {0, 1 ,8 ,9, 16, 17, 24, 25}
J345= {0, 4, 8 ,12, 16, 20, 24, 28}
Необходимым условием для проверки наличия элементов размерности 4 является наличие не менее четырех попарно смежных элемента размерности 3.
(J134, J135, J145, J345)
J1345 = J1+J3+J4+J5-3J* = 1+4+8+16-2*0 = 29
Тогда элемент размерности 4 для опорной вершины J*=0 будут следующим:
J1345= {0, 1, 4, 5, 8, 9, 12, 13, 16, 17, 20, 21, 24, 25, 28, 29}
Очевидно, получить элементы большей размерности не получится.
В качестве опорной вершины возьмем следующую не покрытую вершину, то есть 3 и найдем ее ближайших соседей:
J1=J*
+
(-1)1
20=
3 - 1 = 2
J2=J* + (-1)1 21= 3 - 2 = 1
J3=J* + (-1)0 22= 3 + 4 = 7
J4=J* + (-1)0 23= 3 + 8 = 11
J5=J* + (-1)0 24= 3 + 16 = 19
Таким образом, элементы размерности 1 для опорной вершины J*=3 будут следующими:
J1={3, 1}
J3={3, 7}
J4={3, 11}
J5={3, 19}
Необходимым условием для проверки наличия элементов размерности 2 является наличие более одного элемента размерности 1.
J13= J1+J3-J* = 1+4-0 = 5
J14= J1+J4-J* = 1+8-0 = 9
J15= J1+J5-J* = 1+16-0 = 17
J34= J3+J4-J* = 4+8-0 = 12
J35= J3+J5-J* = 4+16-0 = 20
J45= J4+J5-J* = 8+16-0 = 24
Найдем элементы размерности 2 для опорной вершины J*=0:
J23= (3, 1, 7, 5)
J24= (3, 1, 9, 11)
J25= (3, 1, 19, 17)
J34= (3, 7, 11, 15)
J35= (3, 7, 19, 23)
J45= (3, 11, 19, 27)
Необходимым условием для проверки наличия элементов размерности 3 является наличие не менее трех попарно смежных элемента размерности 2.
(J13, J14, J34) J134 = J1+J3+J4-2J* = 1+4+8-2*0 = 13
(J13, J15, J35) J135 = J1+J3+J5-2J* = 1+4+16-2*0 = 21
(J14, J15, J45) J145 = J1+J4+J5-2J* = 1+8+16-2*0 = 25
(J34, J35, J45) J345 = J3+J4+J5-2J* = 4+8+16-2*0 = 28
Тогда элементы размерности 3 для опорной вершины J*=3 будут следующими:
J134= {3, 1, 7, 5, 8, 9, 12, 13}
J135= {3, 1, 9, 11, 16 ,17, 20, 21}
J145= {3, 7, 11, 15, 16, 17, 24, 25}
J345= {3, 7, 19, 23, 16, 20, 24, 28}
Необходимым условием для проверки наличия элементов размерности 4 является наличие не менее четырех попарно смежных элемента размерности 3.
(J134, J135, J145, J345)
J1345 = J1+J3+J4+J5-3J* = 1+4+8+16-2*0 = 29
Тогда элемент размерности 4 для опорной вершины J*=0 будут следующим:
J2345= {1,3,5,7,9,11,13,15,17,19,21, 23,25,27,29,31}
Очевидно, получить элементы большей размерности не получится.
В качестве опорной вершины возьмем следующую не покрытую вершину, то есть 26 и найдем ее ближайших соседей:
J1=J* + (-1)0 20= 26 + 1 = 27
J2=J* + (-1)1 21= 26 - 2 = 24
J3=J*
+
(-1)0
22=
26 + 4 = 30
J4=J*
+
(-1)1
23=
26 - 8 = 18
J5=J*
+
(-1)1
24=
26 - 16 = 10
Таким образом, элементы размерности 1 для опорной вершины J*=26 будут следующими:
J1={24, 26}
J2={26, 27}
Необходимым условием для проверки наличия элементов размерности 2 является наличие более одного элемента размерности 1.
J12= J1+J2-J* = 24+27-26 = 25
Найдем элементы размерности 2 для опорной вершины J*=0:
J12= (24, 25, 26, 27)
Очевидно, получить элементы большей размерности не получится.
Теперь мы можем построить таблицу элементов функции.
|
X1X2X3X4X5 |
| X | |
0 |
3 |
26 |
|
00000 |
0 |
|
- |
- |
|
10000 |
1 |
j1 |
j2 |
- |
|
11000 |
3 |
- |
|
- |
|
00100 |
4 |
j3 |
- |
- |
|
10100 |
5 |
j13 |
j23 |
- |
|
11100 |
7 |
- |
j3 |
- |
|
00010 |
8 |
j4 |
- |
- |
|
10010 |
9 |
j14 |
j24 |
- |
|
11010 |
11 |
- |
j4 |
- |
|
00110 |
12 |
j34 |
- |
- |
|
10110 |
13 |
j134 |
j234 |
- |
|
11110 |
15 |
- |
j34 |
- |
|
00001 |
16 |
j5 |
- |
- |
|
10001 |
17 |
j15 |
j25 |
- |
|
11001 |
19 |
- |
j5 |
- |
|
00101 |
20 |
j35 |
- |
- |
|
10101 |
21 |
j135 |
j235 |
- |
|
11101 |
23 |
- |
j35 |
- |
|
00011 |
24 |
j45 |
- |
j2 |
|
10011 |
25 |
j145 |
j245 |
j12 |
|
01011 |
26 |
- |
- |
|
|
11011 |
27 |
- |
j45 |
j1 |
|
00111 |
28 |
j345 |
- |
- |
|
10111 |
29 |
j1345 |
j2345 |
- |
|
11111 |
31 |
- |
j345 |
- |
Теперь выделим основные элементы функции. Для этого отсортируем все элементы функции в порядке уменьшения размерности. После этого пометим элементы функции максимальной размерности – они являются основными элементами функции. Затем для всех остальных элементов функции проверим, являются ли они подмножеством основных элементов функции. Если не являются, то их тоже следует пометить, как основные элементы функции.
|
J = 0 |
J = 3 |
J = 26 |
|
j1345 (29) |
j2345 (29) |
j12 (25) |
|
j134 (13) |
j234 (13) |
j1 (27) |
|
j135 (21) |
j235 (21) |
j2 (24) |
|
j145 (25) |
j345 (31) |
|
|
j345 (29) |
j23 (5) |
|
|
j13 (5) |
j24 (9) |
|
|
j14 (9) |
j25 (17) |
|
|
j15 (17) |
j34 (15) |
|
|
j34 (12) |
j35 (23) |
|
|
j35 (20) |
j45 (27) |
|
|
j45 (24) |
j2 (1) |
|
|
j1 (1) |
j3 (7) |
|
|
j3 (4) |
j4 (11) |
|
|
j4 (8) |
j5 (19) |
|
|
j5 (16) |
|
|
Таким образом, мы получили 3 основных элементов функции:
J
= 0: j1345 (![]() )
)
J
= 3: j2345 (![]() )
)
J
= 26: j12 (![]() )
)
Теперь мы можем написать неприведенную систему простых импликант, которая представляет собой дизъюнкцию основных элементов функции:
![]() - неприведенная
система простых импликант
- неприведенная
система простых импликант
Теперь с помощью импликантной матрицы определим, не является ли эта система простых импликант избыточной:
|
|
0 |
1 |
3 |
4 |
5 |
7 |
8 |
9 |
11 |
12 |
13 |
15 |
16 |
17 |
19 |
20 |
21 |
23 |
24 |
25 |
26 |
27 |
28 |
29 |
31 |
|
|
_ _ _ _ _ X1X2X3X4X5 |
_ _ _ _ X1X2X3X4X5 |
_ _ _ X1X2X3X4X5 |
_ _ _ _ X1X2X3X4X5 |
_ _ _ X1X2X3X4X5 |
_ _ X1X2X3X4X5 |
_ _ _ _ X1X2X3X4X5 |
_ _ _ X1X2X3X4X5 |
_ _ X1X2X3X4X5 |
_ _ _ X1X2X3X4X5 |
_ _ X1X2X3X4X5 |
_ X1X2X3X4X5 |
_ _ _ _ X1X2X3X4X5 |
_ _ _ X1X2X3X4X5 |
_ _ X1X2X3X4X5 |
_ _ _ X1X2X3X4X5 |
_ _ X1X2X3X4X5 |
_ X1X2X3X4X5 |
_ _ _ X1X2X3X4X5 |
_ _ X1X2X3X4X5 |
_ _ X1X2X3X4X5 |
_ X1X2X3X4X5 |
_ X1X2X3X4X5 |
_ _ X1X2X3X4X5 |
X1X2X3X4X5 |
|
|
|
+ |
+ |
|
+ |
+ |
|
+ |
+ |
|
+ |
+ |
|
+ |
+ |
|
+ |
+ |
|
+ |
|
+ |
+ |
|
+ |
|
|
+ |
|
|
+ |
+ |
|
+ |
+ |
|
+ |
+ |
|
+ |
+ |
|
+ |
+ |
|
+ |
+ |
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
+ |
+ |
+ |
|
|
Как видно из таблицы все простые импликанты являются существенными. Таким образом, приведенная система простых импликант будет совпадать с неприведенная системой простых импликант.
![]() - приведенная
система простых импликант (минимальная
форма гиперкуба).
- приведенная
система простых импликант (минимальная
форма гиперкуба).
