29.Функция распределения дискретной случайной величины и ее свойства. График функции распределения дискретной случайной величины.
31.Функция распределения и ее свойства.
31.Плотность распределения и ее свойства, связь с функцией распределения
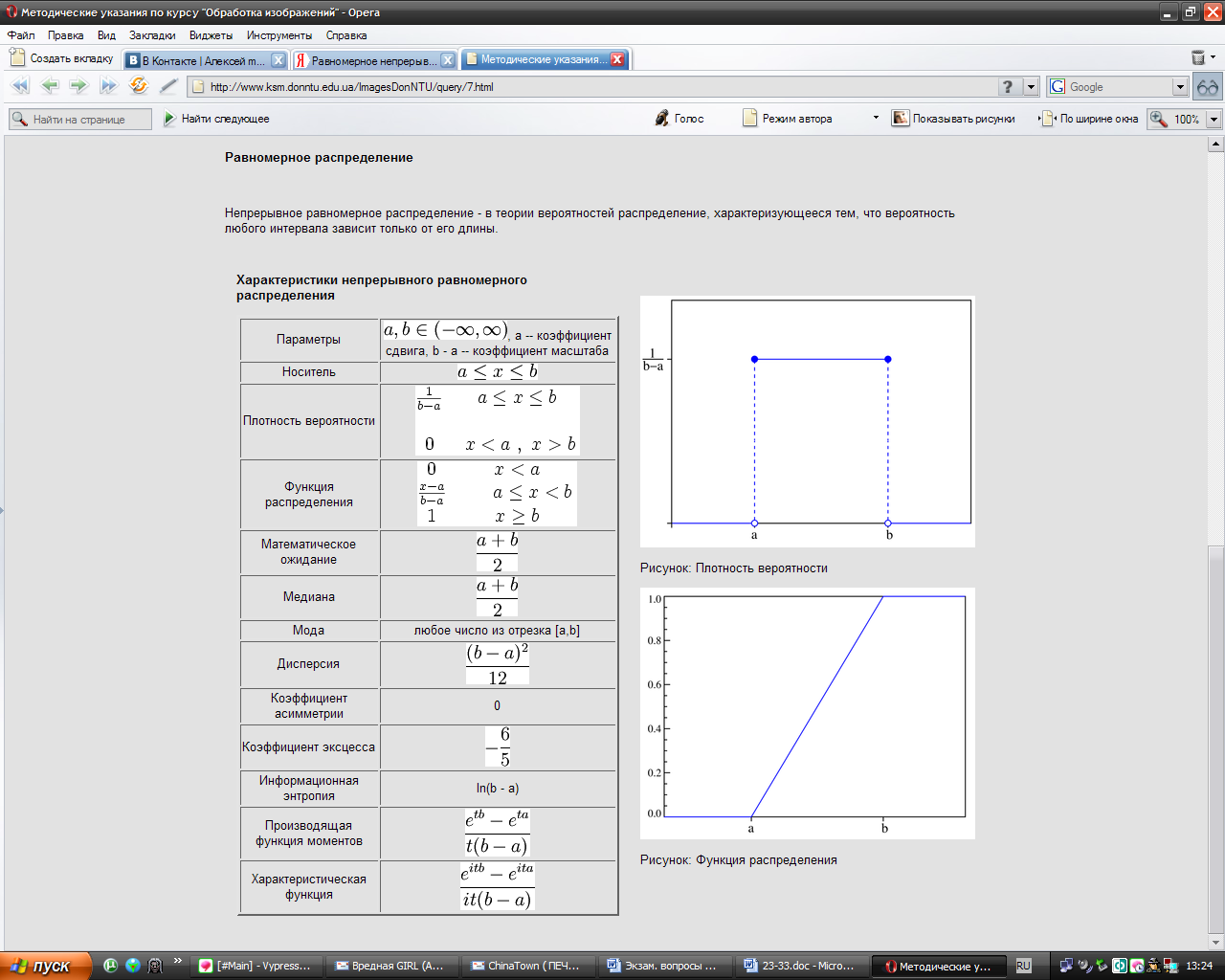
Непрерывная случайная величина x имеет равномерное распределение на отрезке [a,b], если на этом отрезке плотность распределения случайной величины постоянна, а вне его равна нулю, т.е.
где С = Const. Используя условие нормировки 2 из § 9, определим С.
,
откуда с = 1/(b-a) и, следовательно, плотность равномерного распределения имеет вид:
Теперь определим вид интегральной функции распределения для этого закона, который в силу (9.1) будет следующим:
Изобразим графики f(x) и F(x):
Определим числовые характеристики данной случайной величины:
Наконец, найдем вероятность попадания значений равномерно распределенной случайной величины на интервале (a,b) в интервал (a , b ):
Непрерывная случайная величина подчинена равномерному закону распределения, если ее возможные значения лежат в пределах некоторого определенного интервала, кроме того, в пределах этого интервала все значения случайной величины одинаково вероятны (обладают одной и той же плотностью вероятности). С такими случайными величинами часто встречаются в измерительной практике при округлении от счетов измерительных приборов до целых делений шкал. Ошибка при округлении отсчета до ближайшего целого деления является случайной величиной x , которая с постоянной плотностью вероятности принимает любое значение между соседними целыми делениями.
32.Математическое ожидание непрерывной случайной величины. И его свойства
Математическое ожидание непрерывной
случайной величины X,
возможное значение которой принадлежит
отрезку [a,b]
– это определенный интеграл 
(6.4)
Последнее определение (для непрерывной
случайной величины) получено на основании
того, что вероятность попадания X
в интервал приблизительно равна
.
Математическое ожидание случайной величины (как дискретной, так и непрерывной) есть неслучайная (постоянная) величина. Она характеризует среднее значение случайной величины.
Свойства математического ожидания:
M(C)=C – математическое ожидание константы равно самой константе
M(X+Y)=M(X)+M(Y)
Вероятностный смысл математического ожидания:
Математическое ожидание приблизительно равно среднему арифметическому наблюдаемых значений случайной величины:
где:
mk– частота наблюдений, Wk– относительная частота.
Дисперсия и среднее квадратичное отклонение – это числовые характеристики случайной величины, которые позволяют оценить, как рассеяны возможные значения случайной величины вокруг ее математического ожидания.
Отклонением называют разность между значением случайной величины и ее математическим ожиданием, т. е.
xI - M(X).
Пусть закон распределения дискретной случайной величины известен:
X x1 x2 … xn
P p1 p2 … pn
Тогда закон распределения отклонения этой случайной величины имеет вид:
X-M(X) x1-M(X) x2-M(X) … xn-M(X)
P p1 p2 … pn
Так как одни возможные отклонения положительны, а другие отрицательны, то математическое ожидание отклонения обладает важным свойством:
M(X – M(X))=0,
т.е. математическое ожидание отклонения всегда равно нулю.
Поэтому для оценки рассеяния случайной величины вокруг ее математического ожидания вычисляют квадрат отклонения случайной величины, т. е.
(xi - M (X))2.
33.Равномерное непрерывное распределение и его числовые характеристики.
Показательное (экспоненциальное) непрерывное распределение и его числовые характеристики.
С
тандартное
нормальное распределение и его свойства.
37 Асимметрия и эксцесс.
Эксцесс характеризует остроконечность (положительное значение) или пологость (отрицательное значение) распределения по сравнению с нормальной кривой. Теоретически, эксцесс нормального распределения должен быть равен 0. Однако на практике для генеральных совокупностей больших объемов его малыми значениями можно пренебречь. Обычно, если эксцесс положителен, то пик заострен, если отрицательный, то пик закруглен. Эксцесс нормального распределения равен 0.
Асимметричность (коэффициент асимметрии или скоса – s) характеризует смещение распределения относительно математического ожидания. При положительном значении коэффициента распределение скошено вправо, т.е. его более длинная часть лежит правее центра (математического ожидания) и обратно. Для нормального распределения коэффициент асимметрии равен 0. На практике, его малыми значениями можно пренебречь. (термин был впервые введен Пирсоном, 1895)
Осуществим оценку значимости коэффициента асимметрии для распределения NPV. Наиболее простым способом получения такой оценки является определение стандартной (средней квадратической) ошибки асимметрии, рассчитываемой по формуле:
(6.6)
где n – число значений случайной величины (в данном случае – 500).
Если отношение коэффициента асимметрии s к величине ошибки s as меньше трех (т.е.: s /s as < 3), то асимметрия считается несущественной, а ее наличие объясняется воздействием случайных факторов. В противном случае асимметрия статистически значима и факт ее наличия требует дополнительной интерпретации.
Аналогичным способом можно осуществить проверку значимости величины эксцесса – е. Формула для расчета стандартной ошибки эксцесса имеет следующий вид:
(6.7)
где n – число значений случайной величины.
Если отношение e /s ex < 3, эксцесс считается незначительным и его величиной можно пренебречь.
№38