Предмет теории вероятностей

Попробуем ознакомиться с основными закономерностями случайных процессов.

Для начала, возьмем в руки монетку, будем ее бросать и записывать результат последовательно в виде строки: О, Р, Р, О, О, Р. Здесь буквами О и Р обозначено выпадение орла или решки. В нашем случае бросание монетки – это испытание , а выпадение орла или решки – событие , то есть возможный исход нашего испытания.

Пусть мы провели испытание N раз, R раз выпала решка, O = N – R раз выпал орел.

Предположим, что при большом числе испытаний N отношение стремится к некоторой постоянной величине. Назовём её вероятностью p наступления события.

Если существует идеализированный процесс, который можно представить в виде испытаний, и частота случайного события приближается к пределу то этот предел называется вероятностью данного случайного события. Часто вероятность, которая в нашем определении заключена в интервале 0 ≤ p ≤ 1, выражают в процентах, умножая число p на 100 %.

Иногда вероятность события можно предсказать из соображений симметрии. Например, при бросании «идеального» игрального кубика выпадение любой грани равновозможно (равновероятно). Всего граней 6, значит, вероятность выпадения i -й грани p ( A i ) = p ( A 1 ) = p ( A 2 ) = p ( A 3 ) = p ( A 4 ) = p ( A 5 ) = p ( A 6 ) = 1/6.

Если мы имеем дело с измеримыми случайными величинами, например, измеряем в течение нескольких лет количество снега, выпавшего за день, то понятие вероятности тоже можно ввести. Для этого запишем результаты измерения в таблицу с точностью, например, в сантиметр и подсчитаем относительную частоту появления того или иного

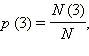
значения. Например, вероятность того, что выпадет 3 см снега, – где N (3) – количество дней, в каждый из которых выпало 3 см, N – общее количество дней, в которые проводились измерения.

Для того чтобы найти вероятность события A , происходящего в серии испытаний, нужно:

найти число N всех возможных исходов (элементарных событий);

принять предположение о равновероятности этих исходов;

найти количество N ( A ) тех исходов, в которых наступает событие A ;

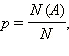
найти частное оно и будет равно вероятности p ( A ) наступления события A .

События. Пространство элементарных событий. Полная группа событий.

Будем полагать, что результатом реального опыта (эксперимента) может быть один или несколько взаимоисключающих исходов; эти исходы неразложимы и взаимно исключают друг друга. В этом случае говорят, что эксперимент заканчивается одним и только одним элементарным исходом.

Множество всех элементарных событий, имеющих место в результате случайного эксперимента, будем называть пространством элементарных событий W (элементарное событие соответствует элементарному исходу).

Случайными событиями (событиями), будем называть подмножества пространства элементарных событий W .

Пространством элементарных событий называют произвольное множество W, W ={w}. Элементы w этого множества W называют элементарными событиями.

Понятия элементарное событие, событие, пространство элементарных событий, являются первоначальными понятиями теории вероятностей. Невозможно привести более конкретное описание пространства элементарных событий. Для описания каждой реальной модели выбирается соответствующее пространство W.

Событие W называется достоверным событием.

Достоверное событие не может не произойти в результате эксперимента, оно происходит всегда.

Невозможным событием называется пустое множество .

Невозможное событие не может произойти в результате эксперимента, оно не происходит никогда.

Случайное событие может произойти или не произойти в результате эксперимента, оно происходит иногда.

Операции над событиями и их свойства.

Суммой событий A и B называется событие, состоящее из всех элементарных событий, принадлежащих одному из событий A или B. Обозначается A + B.

Произведением событий A и B называется событие, состоящее из всех элементарных событий, принадлежащих одновременно событиям A и B. Обозначается AB.

Разностью событий A и B называется событие, состоящее из всех элементарных событий принадлежащих A, но не принадлежащих B. Обозначается A\B.

Статистическое определение вероятности.

Рассмотрим случайный эксперимент, заключающийся в том, что подбрасывается игральная кость, сделанная из неоднородного материала. Ее центр тяжести не находится в

геометрическом центре. В этом случае мы не можем считать исходы (выпадение

единицы, двойки и т.д.) равновероятными. Из физики известно, что кость более

часто будет падать на ту грань, которая ближе к центру тяжести. Как определить вероятность выпадения, например, трех очков? Единственное, что можно сделать, это

подбросить эту кость n раз (где n-достаточно большое число, скажем n=1000 или

n=5000), подсчитать число выпадений трех очков n3 и считать вероятность исхода, заключающегося в выпадении трех очков, равной n3/n – относительной частоте выпадения трех очков. Аналогичным образом можно определить вероятности остальных элементарных исходов – единицы, двойки, четверки и т.д. Теоретически такой образ действий можно оправдать, если ввести статистическое определение вероятности.

Вероятность P(wi) определяется как предел относительной частоты появления исхода wi в процессе неограниченного увеличения числа случайных экспериментов n, то есть

, где mn(wi) – число случайных экспериментов (из общего числа n произведенных случайных экспериментов), в которых зарегистрировано появление элементарного исхода wi. Так как здесь не приводится никаких доказательств, мы можем только надеяться, что предел в последней формуле существует, обосновывая надежду жизненным опытом и интуицией. В практике очень часто возникают задачи, в которых какой-либо другой способ определения вероятности события, кроме статистического определения, найти невозможно или крайне трудно. Непрерывное вероятностное пространство. Как уже

говорилось ранее, множество элементарных исходов может быть более, чем счетным

(то есть несчетным). Так несчётное множество исходов имеет эксперимент,

состоящий в случайном бросании точки на отрезок [a1; a2]. Можно себе представить, что

эксперимент, заключающийся в измерении температуры в заданный момент в заданной

точке тоже имеет несчётное число исходов (действительно, температура может

принять любое значение из некоторого промежутка, хотя в действительности мы

можем измерять её лишь с определённой точностью, и практическая реализация

такого эксперимента даст конечное число исходов). В случае эксперимента с несч ётным множеством W элементарных исходов нельзя считать любое подмножество множества W событием. Следует заметить, что подмножества W, не являющиеся событиями, являются

математическими абстракциями и не встречаются в практических задачах. Поэтому в

нашем курсе данный параграф является необязательным. Чтобы ввести определение случайного события, рассмотрим систему (конечную или счетную) подмножеств пространства элементарных исходов W. В случае

выполнения двух условий:

1) из принадлежности А этой системе следует принадлежность этой системе;

2) из принадлежности и этой системе следует принадлежность AiAj этой системе такая система подмножеств называется алгеброй. Пусть W — некоторое пространство элементарных исходов. Убедитесь в том, что две системы подмножеств:

1) W, Æ;

2) W, А, , Æ (здесь А— подмножествоW) являются алгебрами.

Пусть A1 и A2 принадлежат некоторой алгебре. Докажите, что A1 A2 и принадлежат этой алгебре. Назовём s-алгеброй систему Á подмножеств множества W, удовлетворяющую

условию 1) и условию 2)¢: 2)¢ если подмножества А1, А2,¼, Аn, ¼принадлежат Á, то их счётное объединение (по аналогии с суммированием это счётное объединение кратко записывается формулой ) тоже принадлежит Á. Подмножество А

множества элементарных исходов W является событием, если оно принадлежит

некоторой s-алгебре. Можно доказать,

что если выбрать любую счётную систему событий, принадлежащих некоторой s-алгебре и проводить с этими событиями любые принятые в теории множеств операции

(объединение, пересечение, взятие разности и дополнения), то результатом будет

множество или событие, принадлежащее той же s-алгебре.

Сформулируем аксиому, называемую аксиомой А.Н. Колмогорова.

Каждому событию соответствует неотрицательное и не превосходящее единицы число P(А), называемое вероятностью события А, причем функция P(А) обладает следующими свойствами:

1) Р(W)=1

2) если события

A1, A2,..., An, ¼ несовместны, то =

Если задано пространство

элементарных исходов W, алгебра событий и определенная на ней

функция Р, удовлетворяющая условиям приведенной аксиомы, то говорят, что задано

вероятностное пространство.

Это определение вероятностного пространства можно перенести на случай конечного пространства элементарных исходов W. Тогда в качестве алгебры можно взять

систему всех подмножеств множества W.

Геометрическая вероятность

В одном специальном случае дадим правило расчёта вероятности события для случайного

эксперимента с несчетным множеством исходов. Если между

множеством W элементарных исходов случайного эксперимента и множеством

точек некоторой плоской фигуры S (сигма большая) можно установить

взаимно-однозначное соответствие, а также можно установить взаимно-однозначное

соответствие между множеством элементарных исходов, благоприятствующих событию

А, и множеством точек плоской фигуры s (сигма малая), являющейся частью фигуры S, то , где s – площадь фигуры s, S — площадь фигуры S. Здесь, естественно, подразумевается, что фигуры S и s имеют площади. В частности, например, фигура s может представлять собой отрезок прямой линии, с площадью, равной нулю.

Заметим, что в этом определении вместо плоской фигуры S можно рассматривать промежуток S, а вместо её части s – промежуток s, целиком принадлежащий промежутку s, и вероятность представлять как отношение длин соответствующих промежутков.

Пример. Два человека обедают в столовой, которая открыта с 12 до 13 часов. Каждый из них приходит в произвольный момент времени и обедает в течение 10 минут. Какова

вероятность их встречи?

Пусть x — время

прихода первого в столовую, а y — время прихода второго .

Можно установить взаимно-однозначное соответствие между всеми парами чисел (x;y) (или множеством исходов) и множеством точек квадрата со стороной, равной 1, на координатной плоскости, где начало координат соответствует числу 12 по оси X и по оси Y, как изображено на рисунке 6. Здесь, например, точка А соответствует исходу,

заключающемуся в том, что первый пришел в 12.30, а второй - в 13.00. В этом

случае, очевидно, встреча не состоялась. Если первый

пришел не позже второго (y ³ x), то встреча произойдет при условии 0 £ y - x £

1/6 (10 минут– это 1/6 часа).

Если второй пришел не позже первого (x³y), то встреча произойдет при условии 0 £ x – y £ 1/6.. Между множеством исходов, благоприятствующих встрече, и множеством точек области s, изображенной на рисунке7 в заштрихованном виде, можно установить

взаимно-однозначное соответствие.

Искомая вероятность p равна отношению площади области s к площади всего квадрата. Площадь квадрата равна единице, а площадь области s можно определить как разность единицы и суммарной площади двух треугольников, изображенных на рисунке7. Отсюда следует:

Аксиоматическое определение вероятности.

Вероятностью называется числовая функция, определенная на поле событий S и обладающая следующими свойствами: Аксиома 1. Для любого события A прин. S Р(А)>=0. Аксиома 2. Вероятность достоверного события равна единице Р (омега)=1. Аксиома 3. Вероятность объединения двух несовместных событий равна сумме вероятностей этих событий: А прин. S, В прин. S, А*В=0, Р(А+В)=Р(А)+Р(В). Док-во: Событие А является подмножеством омега, так как А={wi1,…,wim},то, согласно конечной схеме, Р(А)=сумме по l от 1 до m рil, 0<=pil<=1, l=1,…,m, поэтому Р(А)>=0, т.е. условие аксиомы 1 выполняется. Условие аксиомы 2 выполняется, поскольку омега={w1,…,wn}и на основании того, что Р(А)=сумме по l от 1 до m рil, то Р(омега)=сумма по i от 1 до n pi=1. Условие аксиомы 3 также выполняется, так как оно представляет собой содержание теоремы сложения для конечной схемы. Итак, конечная схема является примером объекта, для которого выполняется система аксиом теории вероятностей.

Теорема сложения вероятностей.

Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления: Р(А+В)=Р(А)+Р(В)-Р(АВ). Теорема может быть обобщена на любое конечное число совместных событий. Например, для трех совместных событий Р(А+В+С)=Р(А)+Р(В)+Р(С)-Р(АВ)-Р(АС)-Р(ВС)+Р(АВС). Если два составных события А={wi1,…,wim}и В={wj1,…,wjk} являются несовместными, то вероятность объединенного события С=А+В равна сумме вероятностей этих двух событий.

Условная вероятность. Теорема умножения вероятностей.

1) Условная вероятность события А при условии В равна Р(А/B)=P(A*B)/P(B), Р(В)>0. 2) Событие А не зависит от события В, если Р(А/B)=P(A). Независимость событий взаимна, т.е. если событие А не зависит от В, то событие В не зависит от А. В самом деле при Р(А)>0 имеем Р(B/A)=P(A*B)/P(A)=P(A/B)*P(B)/P(A)=P(A)*P(B)/P(A)=P(B). Вытекает следующая формула умножения вероятностей: Р(А*В)=Р(А)*Р(В/A). Для независимых событий вероятность произведения событий равна произведению их вероятностей: Р(А*В)=Р(А)*Р(В). 3) События А1,А2,…,Аn образуют полную группу событий, если они попарно несовместны и вместе образуют достоверное событие, т.е. Аi*Aj=0, i не=j, U по i от 1 до n Аi=омега.

Вероятность совместного появления двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие уже наступило: Р(АВ)=Р(А)*Ра(В). В частности для независимых событий Р(АВ)=Р(А)*Р(В), т.е. вероятность совместного появления двух независимых событий равна произведению вероятностей этих событий.

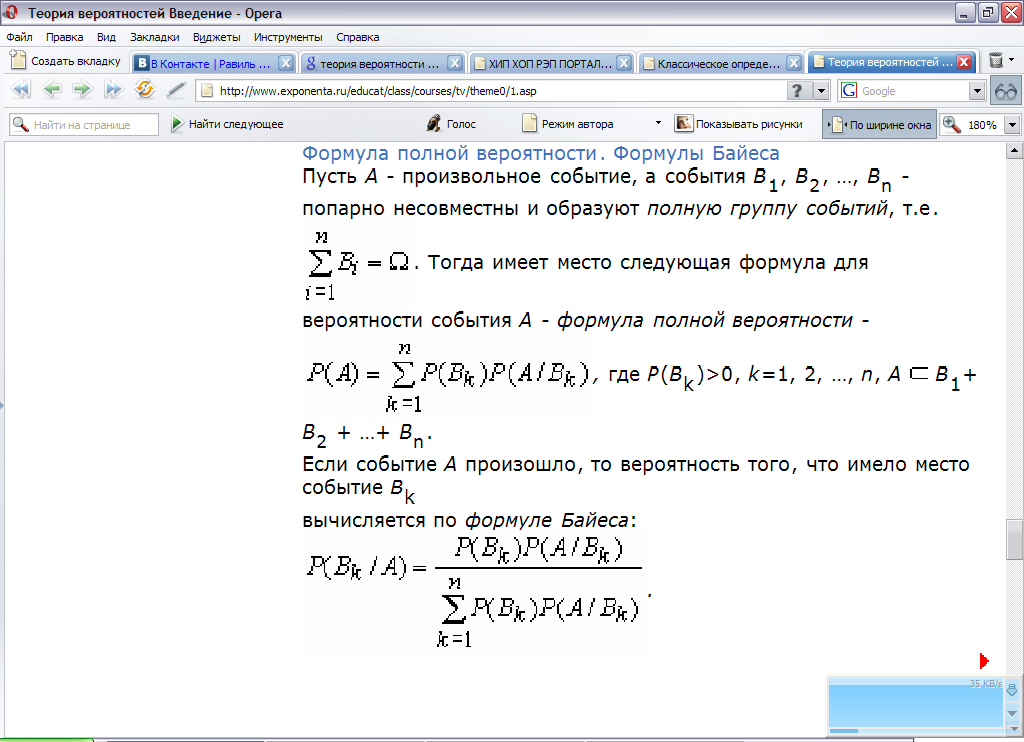
Формула Байеса.

Из формулы полной вероятности легко получить формулу Байеса: для события В с Р(В)>0 и для системы попарно несовместных событий Аi, P(Ai)>0, B прин. U по i от 1 до n Аi . Р(Аk/B)=P(Ak)*P(B/Ak)/сумма по i от 1 до n P(Ai)*P(B/Ai).

Независимые события

События А и В называются независимыми, если появление одного из них никак не влияет на вероятность другого.

Теорема умножения для независимых событий имеет такой вид:

Р(АВ) = Р(А) х Р(В) (1.3)

Иначе говоря, вероятность произведения независимых событий равна произведению их вероятностей.

С логической точки зрения, вероятность произведения независимых событий определяет вероятность сложного события, заключающегося в совместном благоприятном исходе и события А, и события В. Поэтому формула (1.3) называется принципом логического умножения.

Принцип логического умножения позволяет решать множество задач, в которых речь идет о двух и нескольких событиях, так как легко обобщается на произвольное количество событий.

Например, если мы имеем еще и третье событие С, то формула будет выглядеть следующим образом:

Р(А, и В, и С) = Р(А) х Р(В) х Р(С).

Это вероятность того, что обязательно произойдут совместно три события: А, В и С.