
- •Предмет теории вероятностей
- •События. Пространство элементарных событий. Полная группа событий.
- •12. Повторение испытаний. Формула Бернулли.
- •13. Мода биноминального распределения (дописать)
- •14. Локальная предельная теорема Муавра-Лапласа.
- •15.Интегральная теорема Муавра-Лапласа.
- •16. Формула Пуассона и ее применение
- •18.Дискретная случайная величина. Способы её задания.
- •Вероятностные характеристики дискретных случайных величин.
- •Биномиальное распределение и его числовые характеристики.
- •29.Функция распределения дискретной случайной величины и ее свойства. График функции распределения дискретной случайной величины.
- •31.Функция распределения и ее свойства.
- •31.Плотность распределения и ее свойства, связь с функцией распределения
- •32.Математическое ожидание непрерывной случайной величины. И его свойства
- •Правило трёх сигм
- •39. Неравенство Чебышёва
- •Неравенство Маркова ( из этого неравенства следует н. Чебышёва)
- •40. Закон больших чисел. Теорема Чебышева
- •Закон больших чисел
- •46. Вероятность попадания случайной точки в полуполосу, в прямоугольник
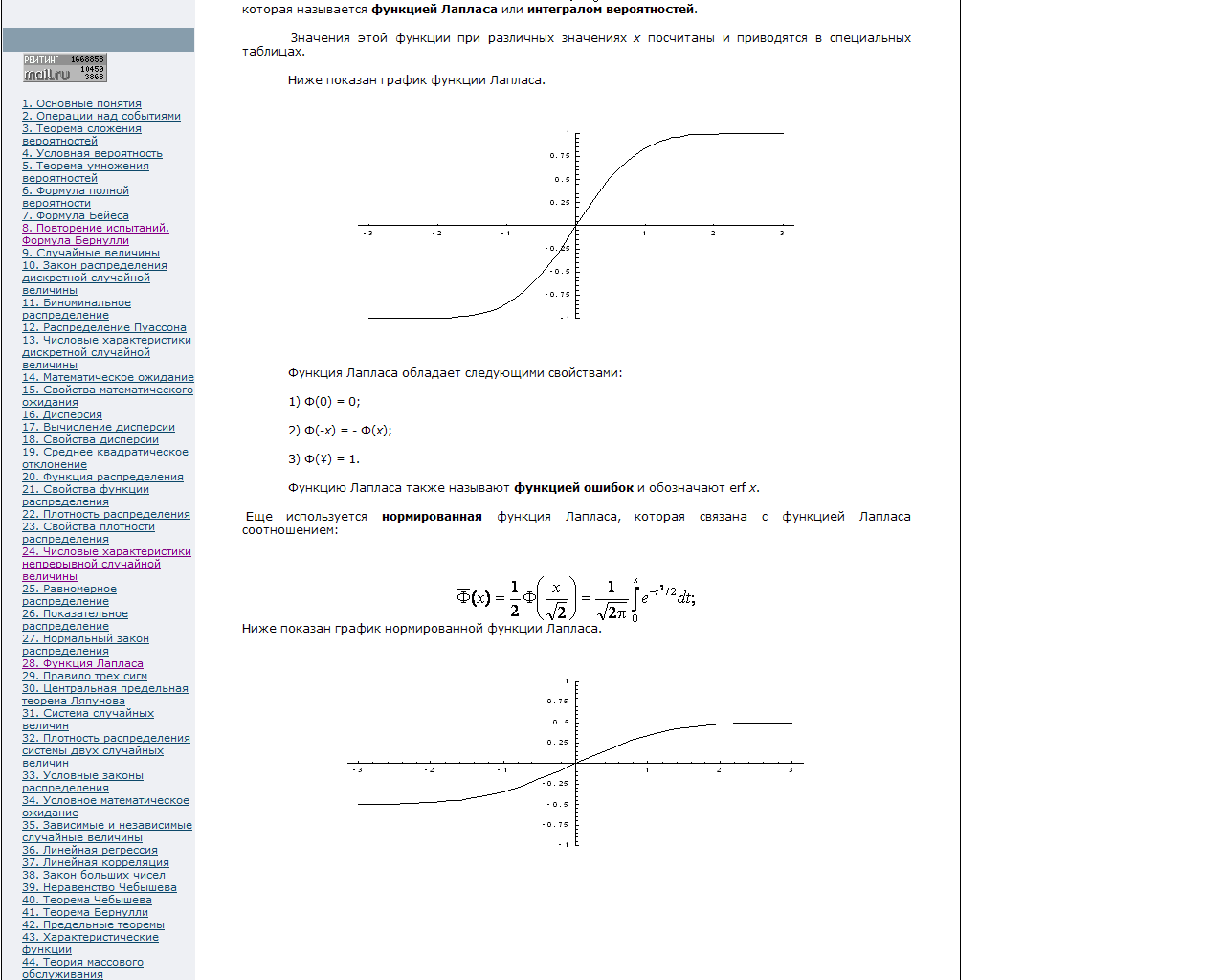
- •49. Коэффициент корреляции и его свойства
- •Свойства коэффициента корреляции
- •51. Линейная регрессия. Прямые линии регрессии
- •Первая модель распределения Пуассона
- •Вторая модель распределения Пуассона
14. Локальная предельная теорема Муавра-Лапласа.
Рассмотрим последов-ть n-нез-ых исп-ий Бернулли
Т-ма: Если вер-ть наступления события А в n-незав-ых исп-ях постоянна и равна р, причем р
не равно 0 и 1, то вер-ть Pn(m) того, что в n-исп-ях соб. А наступит ровно m раз приближенно равна
![]() ,
где
,
где
![]() ,
,
![]() -
Ф-ция Гаусса
-
Ф-ция Гаусса
e=2,7182
Теорема: если вер-ть р появления события А в каждом испытании постоянна и отлична от 0 и 1, то Рn(k) того, что соб-е А появ-ся в n испытаниях ровно k раз, приближённо равна (тем точнее, чем больше n) зн-ю ф-ции Pn(k)=1/(корень из npq)*фи(z). Здесь Фи(z)=1/(корень из 2пи)*е в степени –х*2/2, z=k – np/(корень из npq).Док-во: Рn(k) = P(k<=k<k+1) = 1\корень из 2п ∫(от z1 доz2) e^(-z^2\2)dz = (z2-z1)e^(-z^2\2)\корень из 2п = 1\корень из npq * φ(z)
15.Интегральная теорема Муавра-Лапласа.

16. Формула Пуассона и ее применение
Рассматривается обычная схема биноминального распределения, в котором n - велико, а p - достаточно мало. Тогда точная формула для вероятности появления события A в m испытаниях имеет вид
![]()
Эта формула при больших n вычисляется сложно. Такую вероятность заменяют приближенной
![]()
Для найденного a построим гипотетический ряд вероятностей
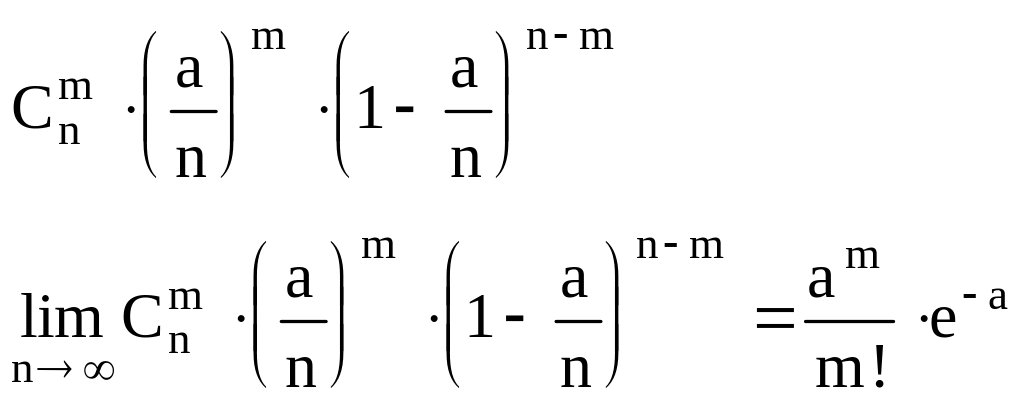
Предполагается, что для достаточно больших n и малых p искомая вероятность
![]()
является членом построенного гипотетического ряда вероятностей, а во вторых находится в малой окрестности предельного значения этого ряда. И, следовательно, это значение можно взять в качестве допустимой хорошей аппроксимации значений искомой вероятности.
18.Дискретная случайная величина. Способы её задания.
Случайная величина называется дискретной, если в результате испытания она может принять значение из конечного либо счетного множества возможных числовых значений.
Случайные величины в дальнейшем будем обозначать большими буквами:
X, Y, Z
Вероятностное пространство дискретной случайной величины задается в виде:
![]() ,
n - конечное или бесконечное.
,
n - конечное или бесконечное.
Пример:
Испытание
- композиция n-независимых испытаний, в
каждом из которых происходит событие
A с вероятностью p, либо
![]() с вероятностью 1-p.
с вероятностью 1-p.
Вероятностное пространство
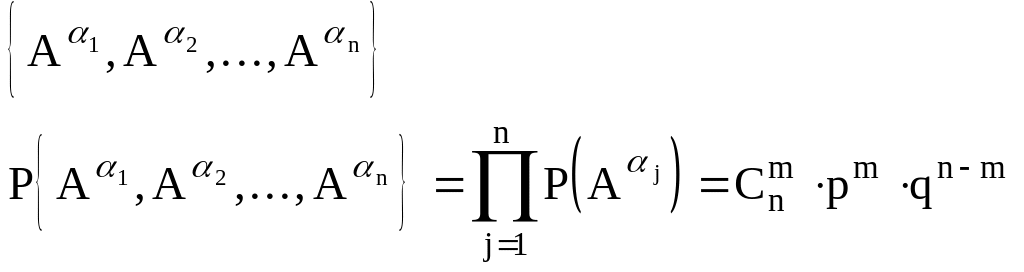
В этом примере -алгеброй является множество всех подмножеств пространства элементарных событий. Введенную нами случайную величину x по определению можно задать:
![]()
- верхняя строчка - это совокупность возможных числовых значений, которые может принимать случайная величина;
- нижняя строчка - вероятность наступления этих числовых значений.
Практически
во всех задачах естествознания отсутствует
промежуточный этап: испытание,
- пространство всех возможных исходов
испытания,
![]() -
числовая скалярная функция, элементы
которой .
-
числовая скалярная функция, элементы
которой .
На самом деле структура:
- испытание;
- исход испытания;
- число на числовой оси.
Вероятностные характеристики дискретных случайных величин.
Математическим ожиданием случайной величины X называется число вида
![]()
xi - все возможные различные конкретные исходы испытания;
pi - вероятности их наступления.
Математическое ожидание является как бы аналогом центра масс точечной механической системы:
![]()
Как центр масс:
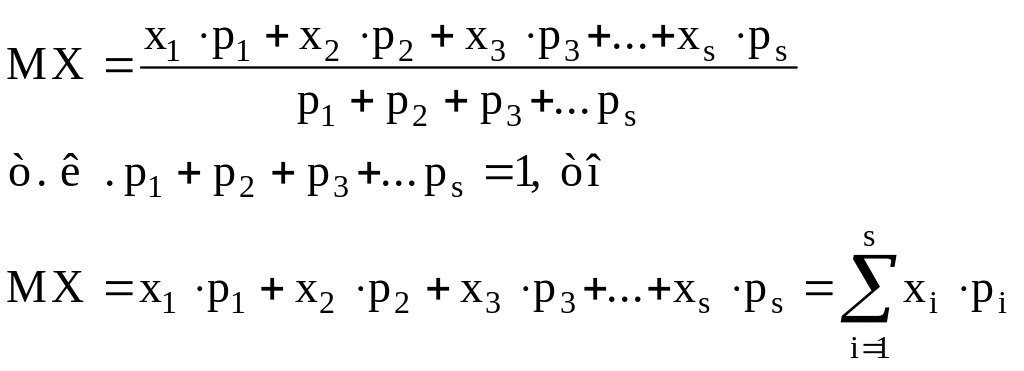
Смысл характеристики мат.ожидания заключается в следующем: это точка на числовой оси, относительно которой группируются результаты конкретных испытаний над дискретной случайной величиной.
