3.3. Линеаризация статических характеристик сау

 

Обычно статические характеристики элементов САУ существенно нелинейных, что затрудняет, а иногда делает невозможным, процесс их исследования и проектирования. Для упрощения решения этой задачи производят реализацию статических характеристик.

Линеаризацией называется замена реальных нелинейных уравнений статических характеристик САУ близкими к ним линейными уравнениями. Для линеаризации характеристик САУ используется метод малых отклонений.

Рассмотрим систему, статическая характеристика которой представляется нелинейным уравнением вида:

.

Графическое представление этой характеристики показано на рис. 7. В установившемся режиме работы САУ на входе и выходе рассматриваемого элемента устанавливаются определенные значения соответствующих сигналов, определяемые режимом работы системы. То есть для любого режима работы с САУ справедливо следующее равенство:

.

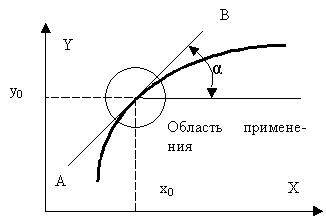
Рис. 6. Графическая интерпретация линеаризации статических характеристик.

 

Функцию, имеющую n непрерывных производных, можно разложить в ряд Тейлора. Эта операция дает следующий результат:

,

где 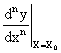— n-ая производная искомой функции в точке установившегося режима работы.

При малых отклонениях от положения равновесия величина . Поэтому все слагаемые разложения в ряд Тейлора будут много меньше, чем два первых. То есть можно считать, что

.

Исходя из этого можно считать, что

.

Из этого выражения следует, что

.

Величина равна тангенсу угла наклона касательной, проведенной к кривой статической характеристики в точке . Это показано на рис. 7. То есть

Следовательно, уравнение линеаризованной характеристики можно представить как:

,

где — коэффициент передачи линеаризованного элемента или системы.

Отсюда следует, что при линеаризации нелинейное уравнение заменяется линейным уравнением в приращениях рассматриваемых переменных.

Аналогичный подход используется, если выходной сигнал устройства является функцией нескольких входных переменных. То есть

.

Для линеаризации статических характеристик такого вида определяют частные производные по каждому входному воздействию.

После разложения в ряд Тейлора получаем, что

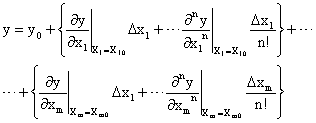
Пренебрегая всеми производными, кроме первых для каждой входной переменной, получаем, что с достаточной степенью точности выходной сигнал элемента определяется как:

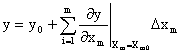
Из этого уравнения следует, что приращение выходного сигнала определяется как

Следовательно, элемент САУ с несколькими входными сигналами может быть представлен как совокупность нескольких линейных элементов и сумматора, объединяющего выходные сигналы этих элементов.

Область применения такого подхода к линеаризации статических характеристик САУ ограничивается наличием непрерывных производных у исходной функции. При наличии разрывов в производных исходной функции, что характерно для элементов с существенно нелинейными характеристиками, такой способ, строго говоря, не применим к точкам, в которых непрерывность производных не обеспечивается.

Для примера рассмотрим линеаризацию статической характеристики вида:

.

Производная этой функции определяется как

.

Следовательно, линеаризованная характеристика рассматриваемого элемента определяется как:

.

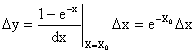Коэффициент передачи линеаризованного элемента определяется как

.