10.3. Определение времени опорожнения резервуаров

Закономерности истечения вязкой несжимаемой жидкости через отверстия в стенках сосудов имеют важное приложение к задачам практики в нефтяной промышленности. Это, прежде всего, задачи о времени опорожнения всевозможных резеруаров и подвиженых емкостей.

Покажем, как, например, вычислить время истечения жидкости из резервуара, форма которого известна. Рассмотрим случай, когда жидкость вытекает в атмосферу через отверстие площадью в дне сосуда. Давление на свободной поверхности принимается равным атмосферному (рис. 10.9).

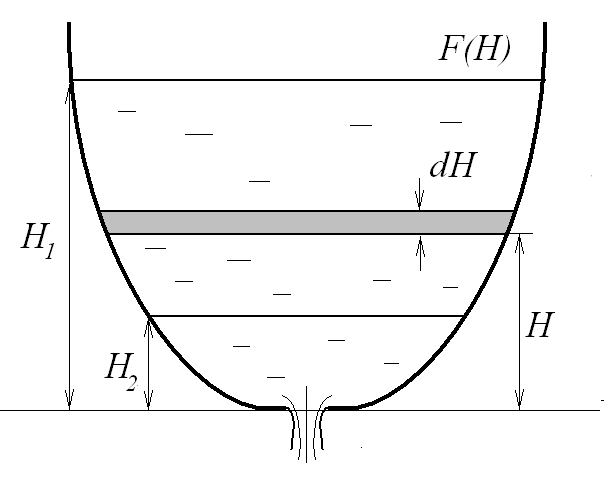
Рис. 10.9. Расчет времени опорожнения резервуара

Движение жидкости в рассматриваемом случае является неустановившимся, т. к. напор изменяется с течением времени, а, следовательно, меняется и расход вытекающей жидкости. В тех случаях, когда истечение жидкости происходит медленно, можно пользоваться гипотезой последовательной смены стационарных состояний.

Смысл этой гипотезы состоит в том, что если уровень жидкости в сосуде меняется медленно, то истечение жидкости в течение каждого интервала времени можно считать установившимся и пользоваться формулой, полученной для расхода жидкости при постоянном напоре

полагая в ней величину равной значению напора в данный момент времени. Таким образом:

. (10.22)

За малый интервал времени уровень жидкости в сосуде уменьшится на величину . Если площадь свободной поверхности жидкости в сосуде обозначить через , то объем жидкости, соответствующий уменьшению уровня жидкости на величину , дается выражением

, (10.23)

причем знак минус в этой формуле берется потому, что при .

Объем жидкости, вытекающей из сосуда, можно выразить по-другому, через расход :

.

Подставляя вместо его выражение, согласно, (10.22), получаем

. (10.24)

Сравнивая (10.23) и (10.24), находим:

,

или

. (10.25)

Для определения времени опорожнения резервуара от уровня до уровня проинтегрируем обе части уравнения (10.25): левую часть по от 0 до и правую часть по H от до . Получим:

(10.26)

Коэффициент , входящий в эту формулу, зависит, вообще говоря, от числа Рейнольдса , которое определяется переменной во времени величиной напора . Поэтому в общем случае интеграл в формуле (10.20) следует вычислять с учетом зависимости . Однако для многих, не слишком вязких жидкостей, величина коэффициента расхода остается постоянной на протяжении всего времени истечения. Рассмотрим случай, когда коэффициент расхода постоянен, тогда:

(10.27)

Если резервуар имеет постоянную площадь сечения (например, призматический резервуар, рис.10.10), то из (10.27) получим:

.

В частности, время полного опорожнения призматического резервуара от уровня до уровня определится по формуле:

(10.28)

В формуле (10.28) в числителе стоит удвоенный объем резервуара, а в знаменателе — расход жидкости из отверстия при постоянном напоре , поэтому

Таким образом, если умножить расход при постоянном напоре на время истечения, то получим удвоенный объем резервуара. Следовательно, для истечения количества жидкости, равного объему резервуара, при переменном уровне требуется время в два раза больше того, за которое вытекает то же количество жидкости при постоянном напоре, равном начальной высоте уровня жидкости в резервуаре.

Пример. Задача об определении времени истечения жидкости из цистерны. Требуется найти время опорожнения круглой горизонтальной цистерны с длиной и радиусом , рис. (10.10) и рис. (10.11).

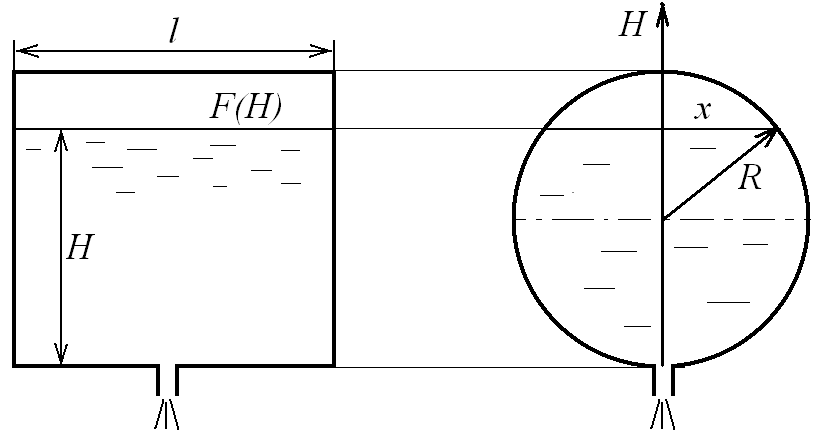
Рис. 10.10. Призматический резервуар

Рис. 10.11. Цилиндрическая цистерна

Площадь опускающейся свободной поверхности жидкости в цистерне записывается в виде

где ,

тогда

(10.29)

Определим время полного опорожнения цистерны, при котором уровень жидкости будет уменьшаться от до . Из общей формулы (10.26) с учетом выражения (10.29) для получим:

. .(10.30)

10.4. Расчет объемных потерь нефти при разгерметизации трубопровода

Еще одним важным техническим приложением теории истечения несжимаемой жидкости через отвертие в стенке сосуда является проблема расчета потерь нефти или нефтепродукта в протяженном резервуаре (трубопроводе) из-за аварии. При нарушении герметичности трубопровода истечение нефти через отверстие происходит, как правило, при переменном напоре. Для продоления жидкостью отверстия требуется некоторая разность давлений внутри трубопровода и вне него, или в терминах напоров - разность напоров . Если размеры отверстия много меньше , говорят о малом отверстии. Расход нефти через малое отверстие выражается, как известно, формулой

, (10.31)

поэтому для вычисления объема вытекшей нефти неоходимо найти величину действующего напора, а фактически – величину давления в том сечении трубопровода, в котором находится отверстие.

Различают три случая [ ].

Первый случай. Площадь отверстия настолько мала, что вытекающая жидкость не создает в трубе сколько-нибудь заметного движения, и нефть в трубопроводе можно считать покоящейся . Тогда для распределения давления в трубопроводе справедлива гидростатическая формула

,

где упругость насыщенных паров нефти; высотная отметка зеркала жидкости в трубопроводе (одинаковая для обеих ветвей трубопровода, расположенных слева и справа от отверстия); высотная отметка сечения, в котором имеется сквозное отверстие. Если при этом внешнее давление равно атмосферному давлению , то

,

где вакууметрическое давление в полости, насыщенной парами перекачиваемой нефти. В терминах напоров последнее уравнение имеет вид:

, (10.32)

т.е. разность напоров, заставляющая вытекать жидкость через отверстие в стенке трубопровода, равна высоте давящего столба жидкости над отверстием за вычетом вакуумметрической высоты, создаваемой разряжением, образующимся в парогазовой полости трубы над зеркалом опускающейся нефти.

С учетом (10.32) формула (10.31) дает для расхода вытекающей нефти выражение

. (10.33)

Формулу (10.33) используют следующим образом. На профиле трубопровода отмечают сечение, в котором находится отверстие, и сечение, в котором профиль трубопровода имеет максимальную высоту. Разность высот этих сечений дает значение, которое входит в формулу (10.33). По мере вытекания нефти высота максимального сечения (теперь зеркала жидкости) уменьшается, так что есть убывающая функция времени: .

Длина столба опускающейся жидкости может уменьшаться как непрерывно, так и скачками - из нее могут исключаться целые участки трубопровода, имеющие образную форму. Это случается всякий раз, когда зеркало нефти сравнивается по высоте с лежащей по ходу движения местной вершиной профиля (рис. 10.12). Например, после достижения опускающимся зеркалом сечения , происходит мгновенная остановка жидкости в образном колене . В сечении столб жидкости разрывается и в этом месте образуется очередная парогазовая полость. Далее зеркало нефти продолжает опускаться, начиная с сечения

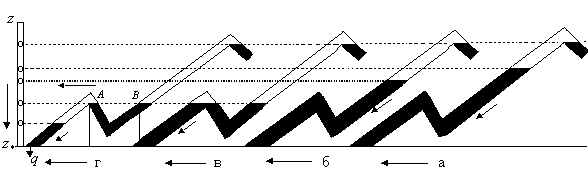
Рис. 10.12. Истечение нефти из рельефного трубопровода

Второй случай. Площадь отверстия в стенке трубы настолько велика, что можно пренебречь разностью напоров внутри и вне трубы в этом сечении, т.е. принять условие , в этом случае предположение о гидростатическом распределении давления неверно. Для отверстий больших размеров разность напоров, входящая в формулу (10.31), не выражается гидростатичесой формулой (10.32). В трубопроводе возникает интенсивное течение нефти к отверстиию, так что значительная часть движущего напора теряется на преодоление внутренних сил вязкого трения.

Поскольку предположение о гидростатике неверно, то процесс истечения жидкости нужно рассматривать в динамике. В рассматриваемом случае расчеты облегчаются тем, что большая величина площади отверстия позволяет считать известным давление внутри трубопровода в том месте, где находится отверстие, а именно, равным давлению вне трубопровода. При свободном истечении нефти в атмосферу это давление равно атмосферному. Скорости нефти в каждой из ветвей трубопровода следует определять из уравнения Бернулли. Имеет место следующая система уравнений:

(10.34)

где координата и геометрическая высота сечения трубопровода, в котором имеется отверстие; координата и высотная отметка зеркала жидкости в левой (от отверстия) ветви трубопровода; координата и высотная отметка зеркала жидкости в правой (от отверстия) ветви трубопровода; коэффициент гидравлического сопротивления, вычисленный соответственно по параметрам течения нефти в левой и правой ветвях трубопровода; d - внутренний диаметр трубопровода; площадь поперечного сечения трубопровода. Для вычисления используются существующие формулы в зависимости от режима течения в левой или правой ветви трубопровода.

Расход нефти вычисляется по формуле

.

Для каждого момента времени из первого уравнения находится скорость течения нефти в левой ветви трубопровода, из второго - скорость течения нефти в правой ветви трубопровода, а затем на основании третьего и четвертого уравнений вычисляются изменения и координат и :

и затем рассчитываются сами координаты и :

Новые координаты зеркала жидкости в трубе позволяют найти соответствующие им высотные отметки и и с помощью уравнений (8.4) повторить весь расчет заново. При этом нужно учитывать также и скачкообразные изменения координат и при отключении образных участков трубопровода, о которых говорилось в предыдущем случае.

Третий (общий) случай. Отверстие в стенке трубопровода таково, что нужно учитывать как течение нефти к месту аварии, так и разность давлений внутри и вне трубопровода. В этом случае процесс истечения из отверстия описывается следующей системой уравнений:

(10.35)

где p_* - давление в месте аварии. При известных значениях и первые три уравнения этой системы позволяют рассчитать три неизвестные величины: и . Два последние уравнения дают возможность найти смещение границ и жидкости в трубопроводе, после чего процесс расчета повторяется.

Напорный режим истечения нефти (т.е. истечения при работающей насосной станции) описывается системой уравнений (10.35), в которой упругость насыщенных паров нефти в первом уравнении заменяется давлением в линии нагнетания насосной станции, расположенной в начале рассматриваемого участка трубопровода, а давление во втором уравнении - давлением в конце рассматриваемого участка. Для напорного режима истечения координаты и равны координатам насосной станциии и конца участка трубопровода, соответственно.