
- •10. Истечение жидкости через отверстия и насадки
- •10.1. Истечение жидкости через малые отверстия
- •Истечение жидкости через малое отверстие в тонкой стенке
- •10.2. Установившееся истечение жидкости через большие отверстия
- •10.2. Истечение жидкости через насадки
- •10.3. Определение времени опорожнения резервуаров
- •Глава 11 течение неньютоновских жидкостей в трубах
- •11.1. Классификаия неньютоновских жидкостей
- •11.2. Ламинарное течение вязкопластичной жидкости в круглой трубе
- •Распределение скорости по сечению трубы
- •Расход вязкопластичной жидкости
- •Коэффициент гидравлического сопротивления
- •Коэффициент гидравлического сопротивления
- •11.4. Турбулентное течение неньютоновских жидкостей
- •12. Неустановившееся течение слабо сжимаемой жидкости в трубопроводе
- •12.1. Прямой гидравлический удар
- •Гидравлический удар в трубопроводе
- •12.2. Общий случай учета инерционных свойств потока капельной жидкости в трубопроводе
- •Амплитуда и скорость распространения волн давления в трубопроводе
- •Защита трубопроводов от гидравлических ударов
- •12.3. Расчет неустановившихся течений жидкости в трубопроводе
- •Дифференциальные уравнения неустановившегося течения жидкости
- •Упрощающие допущения
- •Основные уравнения
- •12.4. Метод характеристик для расчета неустановившихся течений слабосжимаемой жидкости в трубопроводах
- •Начальные и краевые условия; условия сопряжения
Упрощающие допущения
При рассмотрении нестационарных течений многих капельных жидкостей (например, нефтей, нефтепродуктов, воды и т.п.), обычно принимаются следующие допущения и делаются следующие упрощения.
нефть считается слабо сжимаемой жидкостью, т.е. в уравнении состояния
 считается, что
считается, что
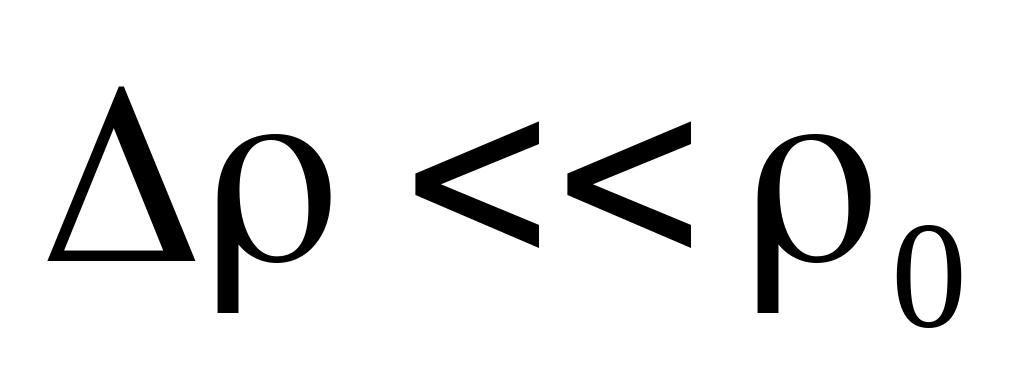 ,
поэтому во всех коэффициентах плотность
нефти заменяется ее невозмущенным
значением;
,
поэтому во всех коэффициентах плотность
нефти заменяется ее невозмущенным
значением;считается, что площадь сечения стального нефтепровода изменяется под воздействием давления крайне незначительно, т.е.
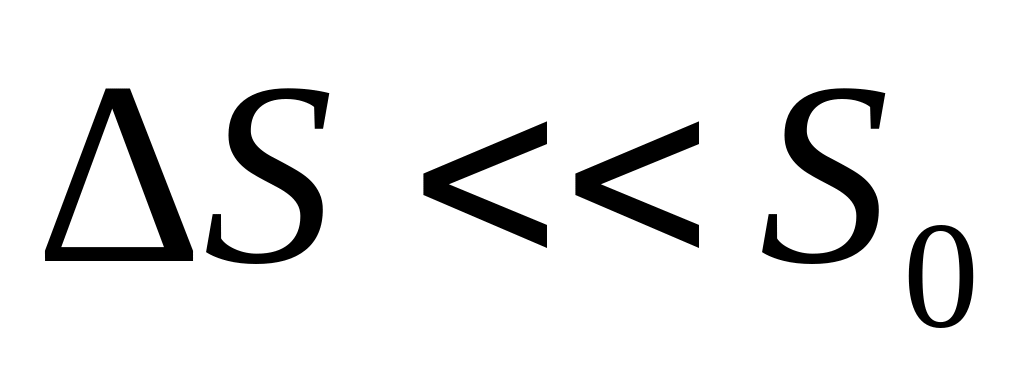 ,
поэтому во всех коэффициентах площадь
сечения трубопровода заменяется ее
невозмущенным значением;
,
поэтому во всех коэффициентах площадь
сечения трубопровода заменяется ее
невозмущенным значением;изменениями величины скоростного напора пренебрегают по сравнению с изменениями пьезометрического напора:
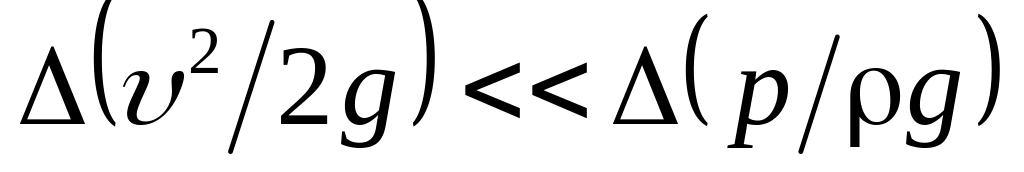 ;
;принимается, что скорость
 течения жидкости в трубопроводе много
меньше скорости
распространения волн давления;
течения жидкости в трубопроводе много
меньше скорости
распространения волн давления;принимается так называемая гипотеза квазистационарности трения, согласно которой
 ,
представленное формулой
,
представленное формулой
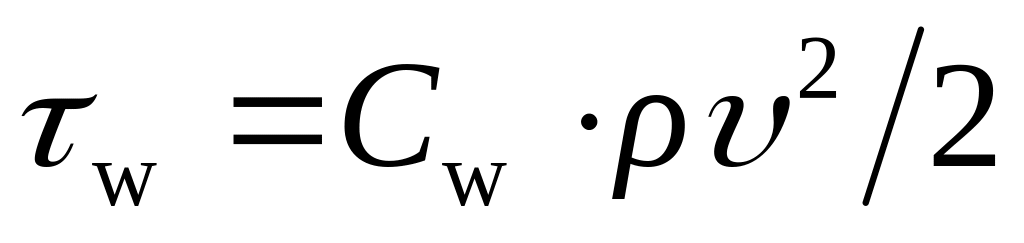 ,
где
,
где
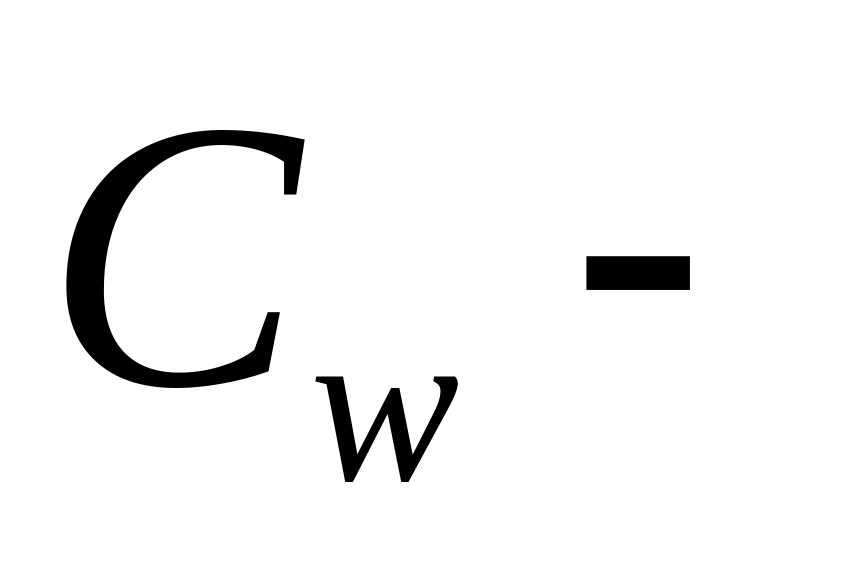 коэффициент трения (или множитель
Фанинга), выражается через коэффициент
гидравлического сопротивления:
коэффициент трения (или множитель
Фанинга), выражается через коэффициент
гидравлического сопротивления:
![]() (т.е.
(т.е.
![]() ),
),
причем для коэффициента используются зависимости, справедливые для стационарного течения.
Основные уравнения
С учетом сделанных допущений уравнение (12.8) преобразуется к виду:
![]() .
.
Учитывая формулы (12.2), (12.4), согласно которым
![]() и
и
![]() ,
,
получаем уравнение
![]() ,
где
.
,
где
.
Можно
показать, что из условия
![]() следует, что
следует, что
![]() .
Тогда уравнение неразрывности получает
окончательную форму:
.
Тогда уравнение неразрывности получает
окончательную форму:
![]() .
(12.12)
.
(12.12)
Уравнение (12.11) также упрощается и принимает вид:
![]() .
(12.13)
.
(12.13)
Таким
образом, мы приходим к основной системе
двух дифференциальных уравнений (12.12)
и (12.13) с частными производными, используемых
для расчета двух неизвестных функций
![]() и
.
и
.
![]() (12.14)
(12.14)
где
![]() .
.
Если
учесть, что
![]() ;
;
![]() и
и
![]() ,
то систему уравнений, определяющих
нестационарное течение нефти в
трубопроводе, можно записать в терминах
объемного расхода
,
то систему уравнений, определяющих
нестационарное течение нефти в
трубопроводе, можно записать в терминах
объемного расхода
![]() и напора
и напора
![]() :
:
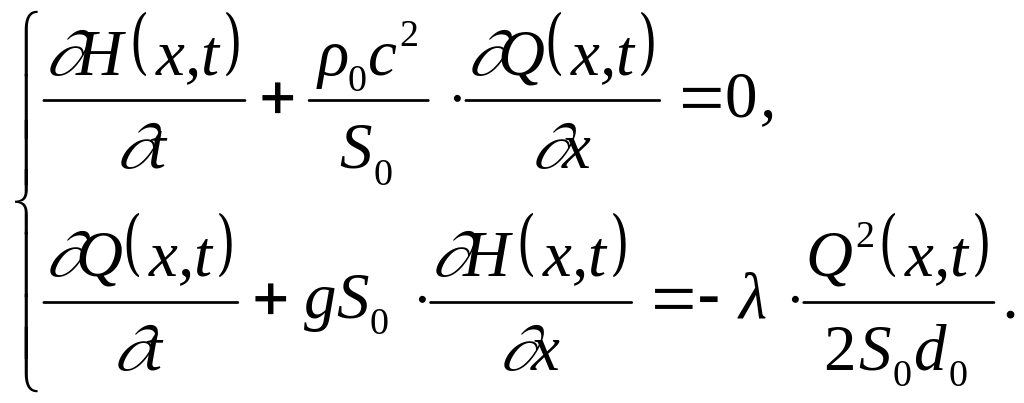 (12.15)
(12.15)
12.4. Метод характеристик для расчета неустановившихся течений слабосжимаемой жидкости в трубопроводах
Расчет неустановившихся течений жидкости в трубопроводах более сложен, чем расчет установившихся течений. Не существует простых алгебраических формул для вычисления параметров течения в неустановившихся течениях хотя бы потому, что таких течений существует бесчисленное множество. Поэтому расчеты неустановившихся течений, например тех, которые были поименованы в начале этого параграфа, осуществляют численно с использованием компьютеров. Приведем один из эффективных алгоритмов расчета, основанный на математическом методе, получившем название метода характеристик.
Умножим второе уравнение системы уравнений (12.14) на и сложим результат с первым уравнением. Получим:
![]() .
.
Аналогичным образом после вычитания второго уравнения системы (12.14), умноженного на , из первого, получим
![]() .
.
Если
на плоскости переменных
![]() рассмотреть прямые линии, которые
определяются уравнениями
рассмотреть прямые линии, которые
определяются уравнениями
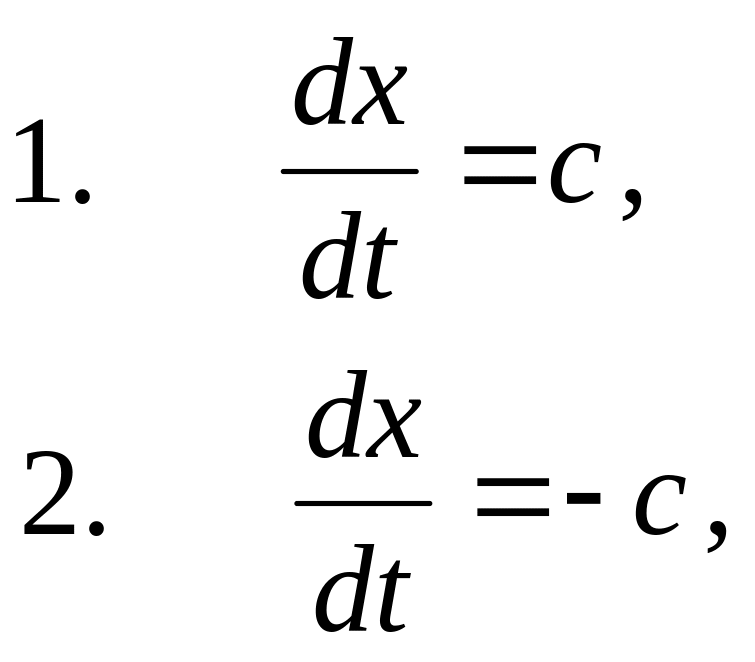
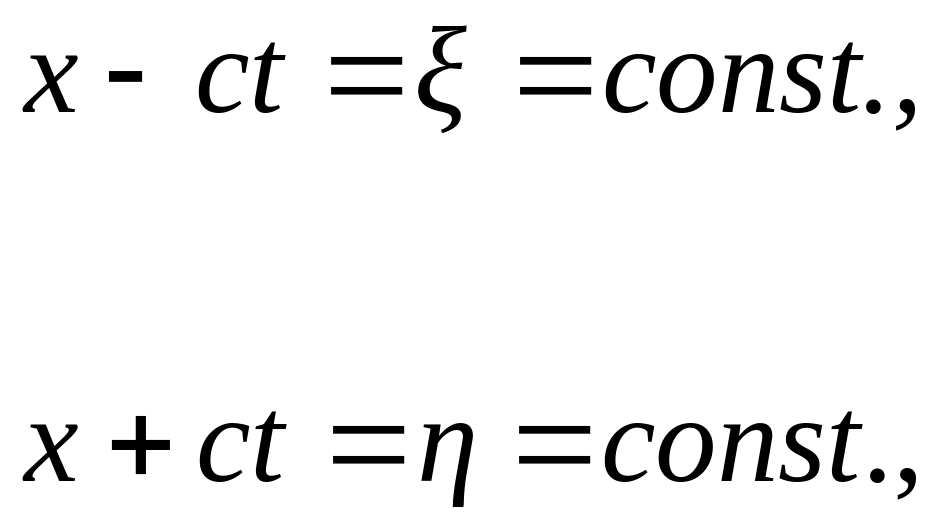
и
которые называются характеристиками
системы
дифференциальных
уравнений
(12.13), можно заметить, что для любого
параметра
![]() :
:
![]()
Это
означает, что выражение, стоящее слева,
есть производная
от функции
по направлению
первой характеристики (или, как говорят,
производная вдоль
характеристики
![]() ).
Аналогично
).
Аналогично
![]() ,
,
т.е.
выражение, стоящее слева, есть производная
от функции
![]() по направлению второй характеристики
(или вдоль
направления
по направлению второй характеристики
(или вдоль
направления
![]() ).
).
Используя понятие производной по направлению, полученные уравнения можно записать в следующем виде:
![]()
или
![]() .
(12.16)
.
(12.16)
Система (12.16) называется характеристической формой системы уравнений (12.14).
Если
![]() ,
то правые части уравнений в (12.15) равны
нулю. Это означает, что вдоль характеристики
положительного наклона (
,
то правые части уравнений в (12.15) равны
нулю. Это означает, что вдоль характеристики
положительного наклона (![]() )
сохраняется величина
)
сохраняется величина
![]() ,
а вдоль характеристики отрицательного
наклона (
,
а вдоль характеристики отрицательного
наклона (![]() )
сохраняется величина
)
сохраняется величина
![]() .
Величины
.
Величины
![]() и
и
![]() называются инвариантами Римана.
называются инвариантами Римана.
Итак,
при
![]() ,
т.е. при отсутствии силы трения и
скатывающей составляющей силы тяжести,
вдоль характеристик положительного
наклона сохраняется первый инвариант
Римана, а вдоль характеристики
отрицательного наклона - второй инвариант
Римана.
,
т.е. при отсутствии силы трения и
скатывающей составляющей силы тяжести,
вдоль характеристик положительного
наклона сохраняется первый инвариант
Римана, а вдоль характеристики
отрицательного наклона - второй инвариант
Римана.
При
![]() величины
величины
![]() и
и
![]() не сохраняются на соответствующих
характеристиках. Однако формулы (12.16)
могут служить для расчета различных
неустановившихся течений в трубопроводе,
особенно если использовать численные
методы.
не сохраняются на соответствующих
характеристиках. Однако формулы (12.16)
могут служить для расчета различных
неустановившихся течений в трубопроводе,
особенно если использовать численные
методы.
Пусть,
например, в какой-либо момент времени
![]() (в частности,
(в частности,
![]() )
в трубопроводе известно распределение
давлений и скоростей течения, т.е. функции
)
в трубопроводе известно распределение
давлений и скоростей течения, т.е. функции
![]() и
и
![]() .
Дадим метод для расчета значений этих
функций в следующий момент времени
.
Дадим метод для расчета значений этих
функций в следующий момент времени
![]() ,
отстоящий от данного на величину
.
Рассмотрим на плоскости переменных
,
отстоящий от данного на величину
.
Рассмотрим на плоскости переменных
![]() прямоугольную сетку с шагом
по координате и
прямоугольную сетку с шагом
по координате и
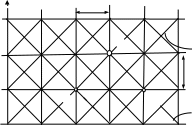
![]() по времени (рис. 12.6).
по времени (рис. 12.6).
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Рис. 12.6. Расчетная схема метода характеристик
Через
узлы получившейся сетки проведем
характеристики
![]() и
и
![]() положительного и отрицательного
наклонов, соответственно. Непрерывное
распределение искомых функций
положительного и отрицательного
наклонов, соответственно. Непрерывное
распределение искомых функций
![]() и
и
![]() заменим дискретными значениями
заменим дискретными значениями
![]() и
и
![]() сеточных функций в узлах построенной
сетки. Предположим, что все значения
сеточных функций в узлах построенной
сетки. Предположим, что все значения
![]() и
и
![]() известны в каком-нибудь слое
известны в каком-нибудь слое
![]() и требуется найти значения сеточной
функции при
и требуется найти значения сеточной
функции при
![]() ,
т.е.
,
т.е.
![]() и
и
![]() .
Покажем, как это сделать на примере
произвольной точки
.
Покажем, как это сделать на примере
произвольной точки
![]() .
.
Заменим
производные по направлению в уравнениях
(16) конечными разностями вдоль характеристик
![]() и
и
![]() .
Получим:
.
Получим:
![]()
где
 .
.
Отсюда
получаем систему уравнений для определения
давления
![]() и скорости жидкости
и скорости жидкости
![]() в точке
в точке
![]() через известные величины этих параметров
в точках
и
:
через известные величины этих параметров
в точках
и
:
![]()
или
![]()
где
![]() и
и
![]() значения
функции
значения
функции
![]() ,
вычисленные по параметрам точек
и
,
соответственно. Из последней системы
вычисляем значения
давлений и
,
вычисленные по параметрам точек
и
,
соответственно. Из последней системы
вычисляем значения
давлений и
![]() скоростей потока нефти в трубопроводе
в момент времени
скоростей потока нефти в трубопроводе
в момент времени
![]() через значения этих же параметров в
момент времени
через значения этих же параметров в
момент времени
![]() :
:
![]() (12.17)
(12.17)
Таким
образом, рекуррентные формулы (12.17) в
принципе решают поставленную задачу о
расчете неустановившихся течений слабо
сжимаемой жидкости в трубопроводе,
поскольку позволяют рассчитать значения
давлений и скоростей течения в последующий
момент времени по известным значениям
этих параметров в предыдущий
момент времени. Так как за первый
“предыдущий” момент времени можно
взять начальное состояние потока (т.е.
значения давлений и скоростей течения
в момент времени, принимаемый за начальный
![]() ),
то вычисляя по формулам (12.17) шаг за шагом
значения этих величин в последующие
моменты времени, можно рассчитать
параметры потока в произвольный момент
времени и затем найти все интересующие
нас технологические параметры
нестационарного режима.
),
то вычисляя по формулам (12.17) шаг за шагом
значения этих величин в последующие
моменты времени, можно рассчитать
параметры потока в произвольный момент
времени и затем найти все интересующие
нас технологические параметры
нестационарного режима.
