Порядок виконання лабораторної роботи:

У додатку №1 подані завдання до цієї лабораторної роботи. У роботі необхідно:

1. Вручну згідно з таблицею завдань зашифрувати вхідне повідомлення шифром Гронсфельда.

2. Програмно згідно з таблицею завдань зашифрувати вхідне повідомлення шифром Гронсфельда.

3. Скласти звіт, у який включити початкові дані, опис послідовності дій шифрування, кінцевий результат і відповіді на контрольні запитання.

Завдання для зашифровки студенти вибирають відповідно до порядкового номеру у списку групи.

Контрольні питання:

1. До якого класу належить шифр Гронсфельда?

2. В чому різниця шифрів простої і складної заміни?

3. Чи зберігається частотна характеристика символів шифртексту після криптоперетворення за методом Гронсфельда?

4. Окремим випадком якої системи шифрування є шифр Гронсфельда?

5. Чи є шифр Гронсфельда надійним з криптографічної точки зору?

2.9. Лабораторна робота №9. Системи з відкритим ключем. Криптосистема RSA.

Тема роботи: Системи з відкритим ключем. Криптосистема RSA.

Ціль роботи: Відпрацювати вміння використання криптосистеми RSA. На практиці зашифрувати текст за допомогою цього алгоритму шифрування.

Загальні відомості

Концепцію систем з відкритим ключем запропонували у 1976 році Діффі і Хеллман.[19] Криптосистеми з відкритим ключем засновуються на використанні особливих властивостей шифрування, що являє собою розрахунок оберненої величини від якоїсь функції, що не може бути реалізована числовими методами.

В сучасній криптографії стандартом де-факто на системи з відкритим ключем є система RSA, спроектована Рівестом, Шаміром та Адлеманом [2].

Теоретичні відомості

Розглянемо математичні результати, покладені в основу алгоритму RSA.

Теорема 1. (Мала теорема Ферма.)

Якщо р – просте число, то

x^p-1 = 1 (mod p) (1)

для будь-якого х, простого відносно р, і

x^p = х (mod p) (2)

для будь-якого х.[1]

Визначення. Функцією Эйлера (n) називається число позитивних цілих, менших n і простих відносно n.

n	2	3	4	5	6	7	8	9	10
(n)	1	2	2	3	2	6	4	6	4

Теорема 2. Якщо n=pq, (p і q – відмінні друг від друга прості числа), то

(n)=(p-1)(q-1).

Теорема 3. Якщо n=pq, (p і q – відмінні друг від друга прості числа) і х – просте відносно р и q, то

x^(n) = 1 (mod n).

Наслідок . Якщо n=pq, (p і q – відмінні друг від друга прості числа) і є просте відносно (n), то відображення

Е_е,n: xx^e (mod n)

є взаємно однозначним на Z_n.

Очевидний і той факт, що якщо е – просте відносно (n), то існує ціле d, таке, що

ed = 1 (mod (n)) (3)

На цих математичних фактах і заснований популярний алгоритм RSA.[4]

Нехай n=pq, де p і q – різні прості числа. Якщо e і d задовольняють рівнянню (3), то відображення Е_е,n і Е_d,n є інверсіями на Z_n. Як Е_е,n, так і Е_d,n легко розраховуються, коли відомі e, d, p, q. Якщо відомі e і n, але p і q невідомі, то Е_е,n являє собою однобічну функцію; перебування Е_d,n по заданому n рівнозначно розкладанню n. Якщо p і q – досить великі прості, то розкладання n практично не здійсненне. Це і закладено в основу системи шифрування RSA.

Користувач i вибирає пару різних простих p_i і q_i і розраховує пари цілих (e_i, d_i), що є простими відносно (n_i), де n_i=p_i q_i . Довідкова таблиця містить публічні ключі {(e_i ,n_i)}.[20]

Припустимо, що вихідний текст

x =(x₀, x₁, ..., x_n-1), xZ_n , 0  i < n,

Z_n-безліч цілих чисел

спочатку представлений по підставі n_i :

N = c₀+c_{i ni}+....

Користувач i зашифровує текст, при передачі його користувачу j, застосовуючи до n відображення Ed_i,n_i :

N  Ed_i,n_i n = n’.

Користувач j робить розшифрування n’, застосовуючи Ee_i,n_i :

N’  Ee_i,n_i n’= Ee_i,n_i Ed_i,n_i n = n .

Очевидно, для того щоб знайти інверсію Ed_i,n_i стосовно Ee_i,n_i, потрібно знання множників n=p_i q_i. Час виконання найкращих з відомих алгоритмів розкладання при n=10¹⁰⁰ на сьогоднішній день виходить за межі сучасних технологічних можливостей [1].

Розглянемо кілька прикладів, що ілюструють застосування алгоритму RSA.

Приклад 1 Зашифруємо повідомлення “САВ”. Для простоти будемо використовувати маленькі числа (на практиці застосовуються набагато більші).

Виберемо p=3 і q=11.

Визначимо n=3*11=33.

Знайдемо (p-1)(q-1)=20. Отже, у якості d, взаємно простої з 20, приймемо наприклад, d=3.

Виберемо число е. Як таке число може бути узяте будь-яке число, для якого задовольняється співвідношення (е*3) (mod 20) = 1, наприклад 7.

Примітка: для простого знаходження числа е досить вирішити в цілих числах рівняння , де а=1,2..n (перебираючи значення n до першого цілого е)

Представимо повідомлення як послідовність цілих чисел за допомогою відображення: А1, У2, З3. Тоді повідомлення приймає вид (3,1,2). Зашифруємо повідомлення за допомогою ключа {7,33}.

C[1] = (3⁷) (mod 33) = 2187 (mod 33) = 9,

C[2] = (1⁷) (mod 33) = 1 (mod 33) = 1,

C[3] = (2⁷) (mod 33) = 128 (mod 33) = 29.

Розшифруємо отримане зашифроване повідомлення C{9,1,29} на основі закритого ключа {3,33}:

M[1] = (9³) (mod 33) = 729 (mod 33) = 3,

M[2] = (1³) (mod 33) = 1 (mod 33) = 1,

M[3] = (29³) (mod 33) = 24389 (mod 33) = 2.

Приклад 2

Шифруємо слово БІГ . Коефіцієнти p=3, q=7.

Визначимо n=p*q=3*7=21. Знайдемо (p-1)(q-1)=12. Виберемо d = 5. Знайдемо число е, для якого справедливо

ed mod ((p-1)(q-1)) = 1.(вирішуємо рівняння де а=1,2...n;) виберемо з безлічі рішень відмінне від числа d число, е = 17.

Представимо шифруєме слово у вигляді послідовності чисел 2 6 4 (порядковий номер букв у алфавіті)

Шифрування по відкритому ключу (17,21):

C₁=2¹⁷ mod(21) = 131032 mod (21) =11;

C₂ = 6¹⁷mod (21) = 16926659444736 mod (21) = 6;

C₃ = 4¹⁷mod(21) = 17179869184 mod (21) = 16.

Отримане зашифроване повідомлення :11 6 16.

Розшифруємо зашифроване повідомлення по секретному ключу (5,21)

М₁= 11⁵mod (21) = 161051 mod (21) = 2;

M₂ = 6⁵ mod (21) = 7776 mod (21) = 6;

M₃ = 16⁵ mod (21) = 1048576 mod (21) = 4.

У підсумку одержуємо вихідне повідомлення БІГ.

Отже, у реальних системах алгоритм RSA реалізується в такий спосіб: кожен користувач вибирає два великих простих числа, і від­повідно до описаного вище алгоритма вибирає два простих числа e і d. Як результат множення перших двох чисел (p і q) установлюється n.

{e,n} утворить відкритий ключ, а {d,n} – закритий (хоча можна взяти і навпаки).

Відкритий ключ публікується і доступний кожному, хто бажає послати власнику ключа повідомлення, що зашифровується зазначеним алгоритмом. Після шифрування, повідомлення неможливо розкрити за допомогою відкритого ключа. Власник же закритого ключа легко може розшифрувати прийняте повідомлення [20].

Особливості методу накладають деякі обмеження на значення деяких змінних. Наприклад: змінна D повинна бути взаємно простою відносно M, тобто ці числа не повинні мати спільних дільників, а змінна E повинна бути такою, щоб залишок від ділення (D*E) на M дорівнював 1.

Порядок виконання лабораторної роботи

1. Повідомлення шифрується вручну посимвольно з використанням алфавіту: _АБВГДЕЄЖЗИІЇЙКЛМНОПРСТУФХЦЧШЩЬЮЯ

2. Після ручного шифрування для перевірки результату необхідно розшифрувати отриманий шифртекст (також посимвольно).

Частина III. Криптоаналіз

3.2. Лабораторна робота № 14. Криптоаналіз шифрів одноалфавітної заміни.

Тема роботи: Криптоаналіз шифрів одноалфавітної заміни.

Ціль роботи: Відпрацювати методи криптоаналізу шифрів одноалфавітної заміни. Провести частотний криптоаналіз шифру одноалфавітної заміни.

Загальні відомості

Шифри одноалфавітної заміни є найбільш старовинними. Перший шифр цього класу застосовувався ще Юлієм Цезарем у I ст. до н.е. Перевагою даного типу шифрів можна вважати досить легку реалізацію як машинним шляхом, так і вручну, недоліком – відсутність будь-якої стійкості до криптоаналізу. [2]

Теоретичні відомості

Шифри одноалфавітної заміни є найпростішими серед інших шифрів заміни. Принцип їхньої дії побудований на тому, що кожній букві відкритого тексту ставиться у відповідність інша, але детермінована (незмінна) буква деякого алфавіту (алфавіту заміни). Через те, що кожній букві відкритого тексту відповідає єдина буква алфавіту заміни, всьому відкритому алфавіту відповідає єдиний незмінний алфавіт заміни, тому шифри цього класу називають шифрами одноалфавітної заміни. [5]

Розглянемо шифр одноалфавітної заміни на прикладі так званого шифру Цезаря. Щоб розібрати і прочитати його тексти, потрібно всякий раз читати четверту букву замість першої відповідно до алфавіту, наприклад Д замість А, при цьому алфавіт представлявся як кільце – наступним за символом Я вважався символ А. Ми розглянемо узагальнений шифр Цезаря, в якому будемо зсовувати символи початкового алфавіту на довільну кількість позицій.

Зашифруємо текст шифром Цезаря при ключі К=5:

Відкритий текст:

У ПЕРІОД РУРСЬКИХ БОЇВ НІМЕЦЬКІ КОМУНІСТИ КОНСТАТУВАЛИ ВІДОМИЙ ФАКТ ЩО НЕОРГАНІЗОВАНІ РОБІТНИКИ ВИЯВИЛИСЯ РЕВОЛЮЦІЙНІШЕ ОРГАНІЗОВАНИХ У ПРОФСПІЛКИ

Шифртекст:

ШФІХМУИХШХЦВПЛЬЄУНЖТМСІЮВПМПУСШТМЦЧЛПУТЦЧЕЧШЖЕРЛЖМИУСЛОЩЕПЧБУТІУХЗЕТМКУЖЕТМХУЄМЧТЛПЛЖЛДЖЛРЛЦДХІЖУРГЮМОТМАІУХЗЕТМКУЖЕТЛЬШФХУЩЦФМРПЛІСЄІХИХУУЄШХІТЛОЮЛСМ

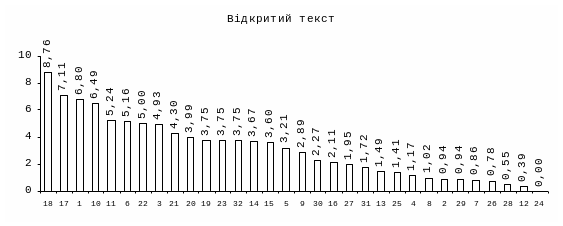
Побудуємо діаграму розподілу частот символів відкритого і шифртексту:

Відкритий текст:

А	Б	В	Г	Д	Е	Є	Ж	З	И	І	Ї	Й	К	Л	М
7	4	8	2	3	8	0	0	2	13	13	1	3	7	4	5
Н	О	П	Р	С	Т	У	Ф	Х	Ц	Ч	Ш	Щ	Ь	Ю	Я
11	15	3	11	5	5	6	2	2	3	0	1	1	2	1	2

Шифртекст:

А	Б	В	Г	Д	Е	Є	Ж	З	И	І	Ї	Й	К	Л	М
1	1	2	1	2	7	4	8	2	3	8	0	0	2	13	13
Н	О	П	Р	С	Т	У	Ф	Х	Ц	Ч	Ш	Щ	Ь	Ю	Я
1	3	7	4	5	11	15	3	11	5	5	6	2	2	3	0

З двох приведених діаграм розподілу частот, ми бачимо, що рядок чисел для відкритого тексту складається з чисел:

7; 4; 8; 2; 3; 8; 0; 0; 2; 13; 13; 1; 3; 7; 4; 5;11; 15; 3; 11; 5; 5; 6; 2; 2; 3; 0; 1; 1; 2; 1; 2

а рядок чисел для шифртексту складається з чисел:

1; 1; 2; 1; 2; 7; 4; 8; 2; 3; 8; 0; 0; 2; 13; 13; 1; 3; 7; 4; 5; 11; 15; 3; 11; 5; 5; 6; 2; 2; 3; 0

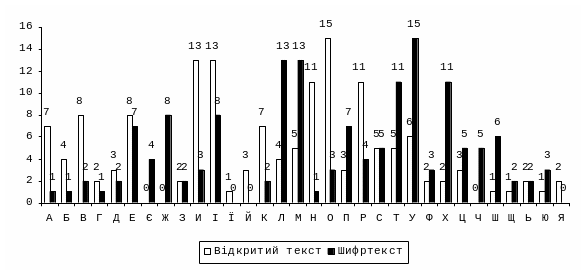
Іншими словами, починаючи з шостого символу, числовий рядок для шифртексту ідентичний початку рядка для відкритого тексту, перші п’ять членів рядка повторюють останні п’ять членів рядка [8]. Побудувавши діаграму, побачимо це в більш наглядній формі:

Рис. 14.1. Діаграма розподілу частот відкритого і шифрованого текстів. Де – відкритий текст; – шифртекст.

Причому порівнювати можна як окремі елементи (О – У (15)), так і цілі групи символів (И, І – Л, М (13)).

Перейдемо до аналізу шифру Цезаря тільки на основі шифртексту. Для цього ми повинні:

• Побудувати діаграми розподілу частот для відкритого і шифрованого текстів у процентному відношенні, оскільки довжина відкритого і шифрованого текстів може відрізнятися.

• Розташувати частоти у порядку зростання.

• Знайти можливі значення ключа як різницю між відповідними значеннями частот. [4]

Приведемо приклад:

Беремо той самий текст, що і в попередньому прикладі і довільний відкритий текст для порівняння його з шифртекстом:

Відкритий текст:

ВЕСНЯНИМРАНКОМЯВІДПРАВЛЯЮСЯПОГУЛЯТИІБРОДЯЧИПОЗЕЛЕНІЮЧИХПОЛЯХПРИХОДЖУВСУСІДНЄСЕЛОТАМЯБАЧУЖИТЕЛІВСЕЛАУСВЯТКОВИХПЛАТТЯХЗМОЛИТОВНИКАМИВРУКАХВЕЛИКОЮТОЛПОЮПРЯМУЮЧИХУЦЕРКВУСПРАВДІСЬОГОДНІНЕДІЛЯІШВИДКАПОЧНЕТЬСЯРАННЯОБІДНЯЯВИРІШУЮПРИЙНЯТИВНІЙУЧАСТЬАЛЕСПЕРШУВІДПОЧИТИНЕБАГАТОНАЦВИНТАРЩООТОЧУЄЦЕРКВУТОМУЩОЯНЕБАГАТОРОЗПАЛЕНІЛИЙХОДОЮУЦЕЙЧАСЧИТАЮЧИРІЗНІНАПИСИНАМОГИЛАХЯЧУЮЯКДЗВОНАРПІДНІМАЄТЬСЯНАДЗВІНИЦЮІЗАУВАЖУЮНАВЕРХІВЦІЇЇНЕВЕЛИКИЙСІЛЬСЬКИЙДЗВІНЩОПОВИННИЙВОЗВЕСТИТИПОЧАТОКБОГОСЛУЖІННЯЯКИЙСЬЧАСВІНВИСИТЬЩЕНЕРУХОМОАЛЕПОТІМПОЧИНАЄКОЛИВАТИСЯІРАПТОМЛУНАЮТЬЙОГОГОЛОСНІПРОНИЗЛИВІЗВУКИДОТОГОГОЛОСНІІПРОНИЗЛИВІЩОЯПРОСИПАЮСЯВИЯВЛЯЄТЬСЯЩОЦІЗВУКИВИДАЄДЗВІНОЧОКБУДИЛЬНИКАЩЕТРЕТІЙПРИКЛАДЯБАЧУЯККУХОННАДІВЧИНАПРОХОДИТЬПОКОРИДОРІВЇДАЛЬНЮТРИМАЮЧИВРУКАХКІЛЬКАДЮЖИНТАРІЛОКПОСТАВЛЕНИХОДНАНАІНШУМЕНІНАВІТЬЗДАЄТЬСЯЩОПОРЦЕЛЯНОВІЙКОЛОНІЩОЗНАХОДИТЬСЯВЇЇРУКАХГРОЗИТЬНЕБЕЗПЕКАЗАТОЧИТИСЯБЕРЕЖИСЯПОПЕРЕДЖАЮЯВЕСЬВАНТАЖПОЛЕТИТЬНАЗЕМЛЮЗРОЗУМІЛОВИПЛИВАЄНЕМИНУЧЕЗАПЕРЕЧЕННЯУЖЕМОЛНЕВПЕРШИЙРАЗЯВЖЕЗВИКЛАІТПТИМЧАСОМЯКЯУСЕЩЕНЕСПУСКАЮНЕСПОКІЙНОГОПОГЛЯДУЗЩОЙДЕІСПРАВДІНАПОРОЗІВОНАСПОТИКАЄТЬСЯТЕНДІТНИЙПОСУДІЗТРІСКОМІДЗЕНЬКОТОМРОЗЛІТАЄТЬСЯНАВКРУГИПОСТАТІСОТНЯМИОСКОЛКІВАЛЕНЕЗАБАРОМЯЗАУВАЖУЮЩОНЕСКІНЧЕННОТРИВАЮЧИЙДЗЕНЬКІТСХОЖИЙЗОВСІМНЕНАТРІСКПОСУДУАНАДІЙСНИЙДЗЕНЬКІТІВИНУВАТЦЕМЦЬОГОДЗЕНЬКОТУЯКЯРОЗУМІЮУЖЕНАРЕШТІПРОКИНУВШИСЬЄБУДИЛЬНИК

Шифртекст:

ШФІХМУИХШХЦВПЛЬЄУНЖТМСІЮВПМПУСШТМЦЧЛПУТЦЧЕЧШЖЕРЛЖМИУСЛОЩЕПЧБУТІУХЗЕТМКУЖЕТМХУЄМЧТЛПЛЖЛДЖЛРЛЦДХІЖУРГЮМОТМАІУХЗЕТМКУЖЕТЛЬШФХУЩЦФМРПЛІСЄІХИХУУЄШХІТЛОЮЛСМ

Визначаємо розподіл частот:

Відкритий текст:

А	Б	В	Г	Д	Е	Є	Ж	З	И	І
6,8	0,94	4,93	1,17	3,21	5,16	0,86	1,02	2,89	6,49	5,24
Ї	Й	К	Л	М	Н	О	П	Р	С	Т
0,39	1,49	3,67	3,6	2,11	7,11	8,76	3,75	3,99	4,3	5
У	Ф	Х	Ц	Ч	Ш	Щ	Ь	Ю	Я
3,75	0	1,41	0,78	1,95	0,55	0,94	2,27	1,72	3,75
Рис. 14.2 Діаграма розподілу частот відкритого тексту.

Шифртекст:

А	Б	В	Г	Д	Е	Є	Ж	З	И	І
0,67	0,67	1,33	0,67	1,33	4,67	2,67	5,33	1,33	2	5,33
Ї	Й	К	Л	М	Н	О	П	Р	С	Т
0	0	1,33	8,67	8,67	0,67	2	4,67	2,67	3,33	7,33
У	Ф	Х	Ц	Ч	Ш	Щ	Ь	Ю	Я
10	2	7,33	3,33	3,33	4	1,33	1,33	2	0

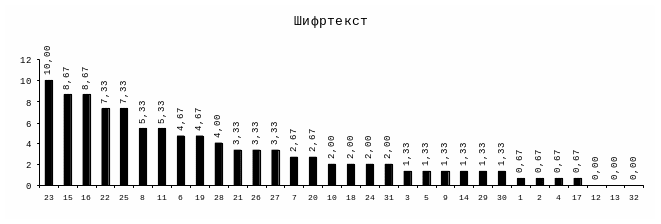
Рис. 14.3. Діаграма розподілу частот шифротексту.

Визначаємо ключ:

Ми бачимо, що між елементами діаграми немає постійної різниці. Це відбувається через те, що шифртекст має досить малу довжину і обчислення частот символів було не таким точним. Тому вибираємо п’ять перших елементів і розраховуємо їх різницю у будь-яких сполученнях:

31	30	30	29	24	22	21	15	15	14	14	13	12
12	11	8	7	6	6	5	5	5	5	4	4

Найчастіше значення, як ми бачимо, дорівнює 5, тому можна з досить великою імовірністю казати, що ключ дорівнює 5. До того ж різниця між найчастішими символами дорівнює також 5.

1. Алфавіт для шифрування: АБВГДЕЄЖЗИІЇЙКЛМНОПРСТУФХЦЧШЩЬЮЯ

3.3. Лабораторна робота №15. Статистичний аналіз багатоалфавітних шифрів на прикладі шифру Гронсфельда.

Тема роботи: Статистичний аналіз багатоалфавітних шифрів на прикладі шифру Гронсфельда.

Ціль роботи: Статистично проаналізувати текст, зашифрований за допомогою шифру Гронсфельда. Закріпити знання про основні особливості багатоалфавітних шифрів.

Загальні відомості

Багатоалфавітні шифри відрізняються від одноалфавітних тим, що одному символу відкритого тексту в різних позиціях може відповідати декілька різних символів в залежності від ключа. Цей факт значно посилює криптостійкість шифрів перед статистичним аналізом, тому що розподілення частот символів в шифртексті стає більш однорідним. [5]

Теоретичні відомості

Так званий шифр Гронсфельда складається в модифікації шифру Цезаря числовим ключем. Для цього під повідомленням пишуть ключ. Якщо ключ коротше повідомлення, то його повторюють циклічно.

Спробуємо скласти таблицю імовірностей зустрічі у відкритому тексті того, чи іншого символу. Імовірність визначаємо за формулою: ,

де N_i – кількість символів L_i у тексті; L – загальна кількість “відомих” символів у тексті.

Текст для аналізу:

НА_СЬОГОДНІШНІЙ_ДЕНЬ_ВІДОМО_БАГАТО_МЕТОДІВ_ШИФРУВАННЯ_В_ЯКИХ_ВИКОРИСТОВУЮТЬСЯ_ВИПАДКОВІ_ЧИСЛА_В_РІЗНИХ_АЛГОРИТМАХ_ВОНИ_МОЖУТЬ_МАТИ_РІЗНЕ_ПРИЗНАЧЕННЯ_НА_ЇХ_ОСНОВІ_ГЕНЕРУЮТЬСЯ_КЛЮЧІ_АБО_НА_ОСНОВІ_КОРОТКОГО_КЛЮЧА_ЩО_ЗАДАЄ_КОРИСТУВАЧ_ГЕНЕРУЄТЬСЯ_ІНШИЙ_СКЛАДНИЙ_КЛЮЧ_ПОТРІБНИЙ_ДЛЯ_ДАНОГО_АЛГОРИТМУ_АЛЕ_В_ЦІЛОМУ_ЗНАЮЧИ_ЦІ_ЧИСЛА_МОЖНА_ПОВНІСТЮ_ЧИ_ЧАСТКОВО_РОЗКРИТИ_ШИФРОВАНЕ_ПОВІДОМЛЕННЯ_ЩО_НЕ_Є_ДОБРЕ_ТОМУ_В_КРИПТОГРАФІЇ_ВЕЛИКУ_УВАГУ_ПРИДІЛЯЮТЬ_ЯКОСТІ_ВИКОРИСТОВУЄМОГО_ГЕНЕРАТОР_ВИПАДКОВИХ_ЧИСЕЛ_ГЕНЕРАТОРА_ВИПАДКОВИХ_ЧИСЕЛ_ПІД_ЯКІСТЮ_БУДЬ_ЯКОГО_ГЕНЕРАТОР_ВИПАДКОВИХ_ЧИСЕЛ_РОЗУМІЮТЬ_СТУПІНЬ_ЗАЛЕЖНОСТІ_ГЕНЕРОВАНОГО_ВИПАДКОВОГО_ЧИСЛА_ВІД_ПОПЕРЕДНЬОГО_ВИДАНОГО_ЦИМ_ЖЕ_ГЕНЕРАТОР_ВИПАДКОВИХ_ЧИСЕЛ_В_ІДЕАЛЬНОМУ_ВИПАДКУ_ЧИСЛА_ЩО_ВИДАЮТЬСЯ_ГЕНЕРАТОР_ВИПАДКОВИХ_ЧИСЕЛ_НЕ_ПОВИННІ_БУТИ_ЗВЯЗАНІ_МІЖ_СОБОЮ_ЯКБИ_ТАК_БУЛО_ТО_ЗЛОЧИНЕЦЬ_НАВІТЬ_ЗНАЮЧИ_ЧАСТИНУ_ВИПАДКОВИХ_ЧИСЕЛ_НЕ_ЗМІГ_БИ_ДАЛІ_ДЕШИФРУВАТИ_ЖОДНОГО_НАСТУПНОГО_ВИПАДКОВОГО_ЧИСЛА_ТОБТО_ШИФРУВАННЯ_БУЛО_Б_АБСОЛЮТНО_НАДІЙНИМ_РЕАЛЬНО_Ж_ОТРИМАТИ_ІДЕАЛЬНИЙ_ГЕНЕРАТОР_ВИПАДКОВИХ_ЧИСЕЛ_ВАЖКО_ХОЧА_І_МОЖЛИВО_ЦЕ_МОЖНА_ЗРОБИТИ_НАПРИКЛАД_НА_ОСНОВІ_ПРИЛАДУ_ЩО_ПЕРЕВОДИТЬ_У_ПОТРІБНУ_ФОРМУ_АБСОЛЮТНО_ВИПАДКОВУ_ШВИДКІСТЬ_ВІТРУ_У_ДАНОМУ_МІСЦІ_АБО_НА_ОСНОВІ_ПЕРЕВОДУ_У_ЧИСЛА_ІНТЕРВАЛІВ_МІЖ_НАТИСКАМИ_КОРИСТУВАЧА_НА_КНОПКИ_КЛАВІАТУРИ_ПЕРСОНАЛЬНОГО_КОМПЮТЕРА_ТЕЖ_АБСОЛЮТНО_ВИПАДКОВІ_ПОСЛІДОВНОСТІ_ЯКЩО_ЗАДАТИ_ОДИНИЧНИЙ_ІНТЕРВАЛ_ДОСТАТНЬО_МАЛИМ_АЛЕ_ОСНОВНА_ПРОБЛЕМА_НЕ_В_ПРОЦЕСІ_ОТРИМАННЯ_НЕЗАЛЕЖНИХ_ВИПАДКОВИХ_ЧИСЕЛ_БАГАТО_ШИФРОВОК_ПРОСТО_НЕ_ЗМОЖУТЬ_БУТИ_РОЗШИФРОВАНІ_ЗАКОННИМИ_КОРИСТУВАЧАМИ_ЯКЩО_ЗАШИФРОВАНІ_СПРАВЖНІМ_ГЕНЕРАТОР_ВИПАДКОВИХ_ЧИСЕЛ

Таблиця 15.1. Розподілення імовірностей появи символів у відкритому тексті

Відкритий текст
Символ	Частота	Імовірність	Символ	Частота	Імовірність
1	2	3	4	5	6
_	212	0,135	Н	96	0,061
1	2	3	4	5	6
А	114	0,073	О	152	0,097
Б	22	0,014	П	40	0,026
В	81	0,052	Р	65	0,042
Г	30	0,019	С	53	0,034
Д	48	0,031	Т	69	0,044
Е	67	0,043	У	40	0,026
Є	4	0,003	Ф	9	0,006
Ж	15	0,010	Х	15	0,010
З	20	0,013	Ц	7	0,004
І	107	0,068	Ч	30	0,019
Ї	54	0,035	Ш	10	0,006
И	2	0,001	Щ	6	0,004
Й	7	0,004	Ь	22	0,014
К	48	0,031	Ю	17	0,011
Л	50	0,032	Я	19	0,012
М	34	0,022

Проаналізуємо цю таблицю. Найчастішим символом у будь-якому тексті є пробіл (його імовірність становить десь 14-19%), інші символи (О, А, Е, І) дещо менш імовірні (десь 5-10%). Тому ми можемо зробити висновок, що найчастіші символи у тексті, зашифрованому за допомогою шифру Гронсфельда, отримані переважно з пробілу. Якщо використовувався ключ,

, а код пробілу в алфавіті дорівнює 1, то найчастішими символами у шифрованому тексті будуть символи:

.

Однак через те, що ключ накладається на повідомлення циклічно, символ може бути отриманий з символів:

,

але їх імовірності значно менше імовірностей пробілу, тому вони накладають на перетворення невелике викривлення. Взагалі сума імовірностей отриманих символів дорівнює:

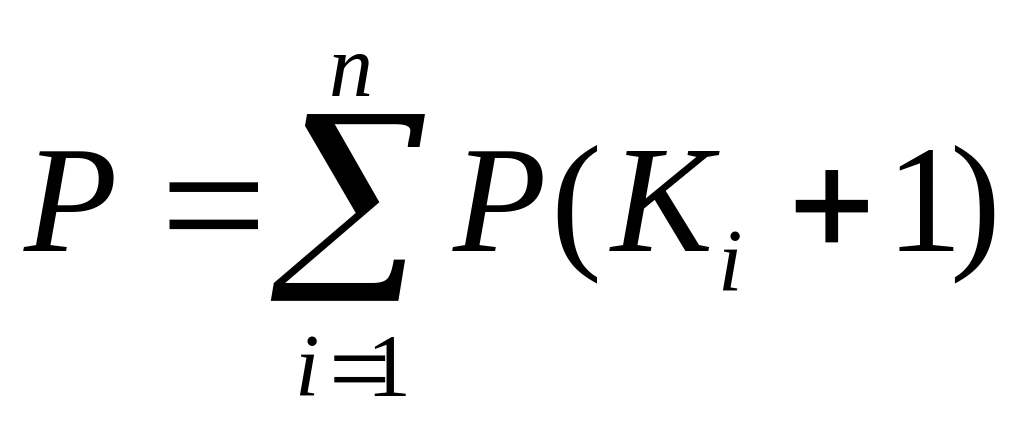
При цьому, якщо Р(1) – імовірність пробілу у відкритому тексті, то Р>Р(1). Однак, якщо ми знайдемо відношення , то побачимо, що при однаковому n (довжина ключа) для різних текстів .

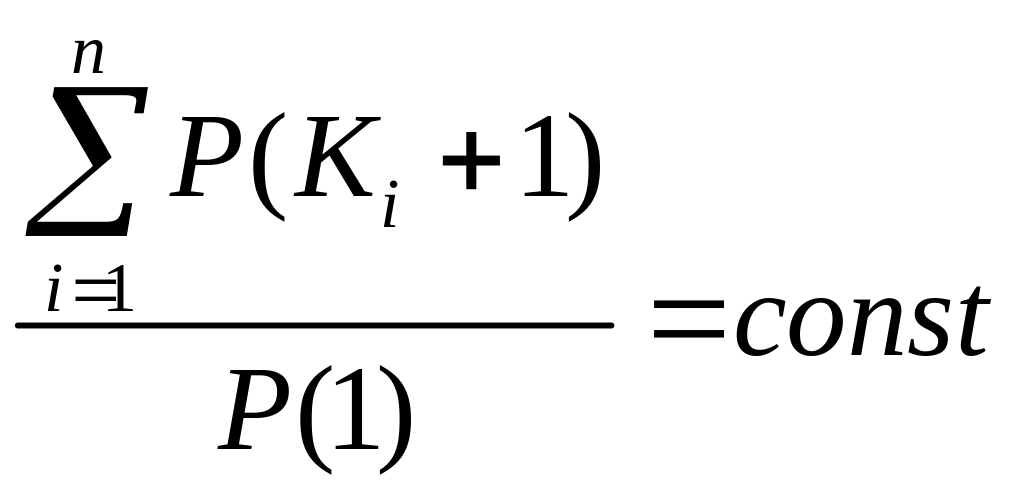Таким чином, знаючи межі зміни елементів ключа K_i, а також розподілення імовірностей символів у цих межах, ми можемо знайти елементи ключа, вибираючи перші n найчастіших символів.

Для того, щоб розрахувати довжину ключа, проаналізуємо розподілення імовірностей перших k (межі зміни елементів ключа K_i) символів, починаючи від базового (в найпростішому випадку k=10, базовий символ – пробіл). Використаний при шифруванні алфавіт:

_АБВГДЕЄЖЗИІЇЙКЛМНОПРСТУФХЦЧШЩЬЮЯ

Шифрований текст (код 314)

ЩЇІЛАЖКРТХЄЙЙАСЗНДИАСК_ОСЙГКТЦЙОКВОИПБІВБЕФППАУСЙЦГЕМДФУКЕПХХЄНВСИЬЄНВОЛВСИЬЇГЕАХСВЛВЧИВТДПЄГТПГФПЕКАЦКМАНІГРЇЖКМЛЇНГКАУУІЦКНОУБНРЇНВГЛРАЕГШКХЮГЩЇСРЇХХЮГУЄЮЗКГФБРЗАЄВУЛПА_САЬЙНГЩЇСРПХХ_РВОИЕЇЗТПЄКЕДИАЛВОИВГЛЖРТЕЇЗГМТВОЛБЛТЛАФЗБП_ОТФУЛВБПЗА_САЄСОКТСИЖТЦГГПБЯЦ_АПЙЩИВТКПРЦСНГФІПЙАСГАХХПФСОЛВЧЛРОТФУЛВЬТВГХХБССГПАЖХТСТЯЄСР_ГЇАРЗУТААЇЙУЦБЧЛРОТФУЛВЇГЛЦСКАЙПЇСЙАОСЩЦЦЯЦ_АЧВИЄБИОЦАЙКАЙУПХХБСР_РВТКОІГСТТДІЧФУДРБЄОІЄГЯ_ЗДТВЧЛРОТФУЛВТЦЦРЛРЮГРЄЄКСВВГТОЇГЖФЩЦА_САЗСРЧФЛДИУАФ_ВНАРКСВОПГЇСТФУДРОВВТКОІГРЇЖКМЛЇНГБЛГКЕИГМГЕІ_СЙГППЖЦУССТЦКСТЇФРЦАСГЕПЙЩОЦАЇЙУЦБАЮГТЦЙОТААФЦКСКГСЙКГЬБХХІССЯЛУПСКШСЙК_САІВГЛУФЄГОСБАВНАЄЙОКНБІВГТРПГЦТВНЄГЕЇФЦГДРОВВЖГЕІЙРБСР_ЮСДТВОИДФЗ_АЙГА_ЙСИВЛФГКС_ПБВХТУНТААСКДЛОЇЙПФГДФЄВВКВУТМАУСДПБЕГЯПЧФ_ОЗАЄКСЧЕБСР_ГЦТВНЄГЕІЙРБСР_ГЬПЖСАСЗВЧЖЮГЇБ_ЙСИВОИПІСЦШИВМТІОТВУТПФГЯПГЇПЄФЇРВОИВЇХРФІВЬКУПЖСАХЕЇЦЦПЦІЄГЩЄГКМБЇЇВВРИУТУЗЛЦЙГКВЕЇЗСИОПГБЛТЛАЧНМДЖЄСЙКГЦАСГТХГНКШАТФЛЛОЮОЙАРЙАУСТЦККССАРГЖРСАУСУФЗВЧВГГДЇП_ЩГЕФЙ_ЛТПФГФЛТУПЮЗОТПФХТСТЯЄССНЧВТЄКУЛВБГТПЦКНГПЇФЙМТПАСГЩКШАХЙМГФМЧІІЦ_АЦЗАВНПБВНЛУПБВНТІЄРСНКВОИВДКРФЮЙАЄКЕГЩЮТЄПГЕІЙРБЦЙАЬААЛОЯЙСССКТЦ_АЛВЧБВОИСВЩКЕСКТЦ_АСЗРФГГЗЙУДНІНВОЛЄЇПКИРВ_ОВИДТЄФЗШИРОВВЬКУПЖСАХЕЇЦЦАЕЦУЦБАРКДГДІГДФЦЙВТІЄХХГИРОКПАТДСДЇПРВЕЧПЛКБЛ_САРЙАЛВСТЇШДУПЄГОЛВУТВОИВТЦСТТЕОТВЗКХУВВФГРБХВМКЮЄЄКЕОУІПЙТВВПЮКАСГАЕГЗДРПХХЇГЦТЛШАЄЙЕЛЕАЙВДПЦИПЙГТААЙОЇХХЯГЖІЄЙНТФ_СГАЦЗА_САСГИКЕБІХЮХБАЛЖЄДОБРЙАРЙАСЗЦЦЦЖРСАХЗВИВМКЮЄГЇБГХЄГЯПГРЄЙГГЇЖІГППЇЗНТВРФЙЕЧЮІЦЙАЄВТТДЇГХПНВОИОЄЖНІНВСЧШАУСШЧХУЛЕА_СОДЇІЄГЖЦ_ТВВЇЗЗБПКИРСНГЖФФРБГЇГКЬЛДВТКОЮСКЩИВОЛІАЖРЇЄЇОИЕЇФЗОТЄПЧВ_ОЙКГПЇФГАСКДЛОЇЙПАЯСРИРДДЦСДВФХЗА_ЗАІВОДФМЛЖЛТПАЦСДТВЗЛЖЄДОФГЯПГФУЄССКЕАЩУІХХІВРТАНІНВУИЛИРВТЦЦРЛРЮГЦРИЕОИРПХХЇГТПЄКЕССЩИРОБВЕТВГКЯІЩВПЕИЛЦКГГДБЇГОАВГКЯІРВЧЛРОТФУВПАЄЙЬЛМАЗСТОСОДОПХХЇЕЦМДВУДНАЄЗМКНБГЯПГЧЇПСТТЧІГЕІЩСЕКОІГЇАСЗАГВ_ОВИГГВХСМБХОТЛФУЗГСЗОТФУЛВВТЄАСГАЄЗСЯЙОЛВ_ОВЕДРБГКТЦЙОДВФУСЕЛДОКХІХБАЕСДТЕЇЙОІЦЙТВВИГДПЖСНГЦАУУПЗСГЇЗОСКАЦЙТВЬПФКШГЩЄГДФПЙАХГНЛВОДЛГСКАЛЦВИЖІЦЗМАРЄНЮІИВПЕИЛЦЙАЕГЗДРЮГВБПЗАЦЗА_САУЗСИНПСЦЖГХІРВТДПІРВЬИВОИФУДИА_ЙСКПАЄСОТВУЛОЮОЙАУЗСИНПСОІЄСАУУІРКУОГАЗО_ГСТПКГРЙАФСИЧЬІПЙТВВГКЇОДЕБЦЙАЙГАЬЙНГОБЗСНГКЕИГМЛЕАЦГЛТІАЛВСИГМАРЇХХЮТФПЕЙАРЙАХХБПЙАДХЄМФУДПІГГМИВЦЛДБГПІГЕЇЗУЄООІХБАЄКЕГФБРСДТВЇЗЗБПЦПХХБСРЇГПЄЦГХЛЇІОЙАЄОБХРЄГНБЇЦШКВТУУБЄЙАЧФЄГЯЄГФБРЗАЄВОАСНЧВЩЧНББХЮГЯІФЦСИГМАРЇХХЮГУЇЮВФГФПЕКАХХПХСГССАВНПМВГХЗАЛРЩИВНДИМКЮЄГЦЕДЕБСЗАЛФОЧЕБСР_ГГМИВЕТЄНДХПРВЙЩВИДОІЯЙМТФ_ГХЄГТППСЗИРОВВЬТВГЄЙЕЧВ_ЄРПМВОИЕЇЗТПЄКЕССТЦКАСГЩТЄПГФГЛХФГБГКЯАХНБЙГОТПФГКЕИГМТЕЇ

Таблиця 15.2. Розподілення імовірностей появи перших 10 символів у шифрованому і відкритому тексті

Шифр текст
Символ	Частота	Імовірність	Символ	Частота	Імовірність
_	43	0,027	Н	51	0,033
А	139	0,089	О	98	0,063
Б	65	0,042	П	105	0,067
В	146	0,093	Р	89	0,057
Г	171	0,109	С	140	0,089
Д	62	0,040	Т	111	0,071
Е	65	0,042	У	65	0,042
Є	74	0,047	Ф	72	0,046
Ж	28	0,018	Х	73	0,047
З	57	0,036	Ц	78	0,050
І	65	0,042	Ч	29	0,019
Ї	59	0,038	Ш	12	0,008
И	68	0,043	Щ	22	0,014
Й	77	0,049	Ь	16	0,010
К	92	0,059	Ю	26	0,017
Л	76	0,049	Я	21	0,013
М	32	0,020

Ми бачимо, що декілька точок відстоїть від інших на деякій відстані (В,Г,А), і становить окрему групу. Можна із впевненістю стверджувати, що вони були отримані саме з пробілу (у код входять цифри 3,1,4).

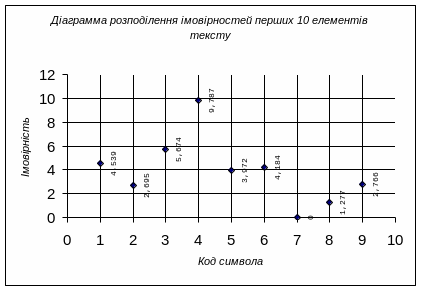
Рис 15.1. Діаграма розподілу імовірностей перших 10 елементів тексту.

Сформулюємо алгоритм аналізу:

• Складаємо розподілення імовірностей елементарних частин тексту.

• Вибираємо базовий символ (символ з найбільшою імовірністю у відкритому тексті).

• Окремо виписуємо перші k символів, починаючи з базового (k – найбільше число на яке може змінитися базовий символ).

• Сортируємо ці k символів, починаючи з найчастішого.

• Послідовно, починаючи з найчастішого символу, знаходимо елементи ключа як різницю між кодом символу та кодом базового символу.

Таким чином ми можемо знайти деякі елементи ключа. Через те, що близько до пробілу знаходиться ще декілька символів, що у відкритих текстах мають порівняно високі імовірності (А, Е та ін.), неможливо однозначно встановити всі елементи коду. Тому аналіз необхідно виконувати у декілька раундів, міняючи при цьому базовий символ (О, Е).