5.2. Основы теории ортометрических, нормальных и динамических высот.

П роцесс геометрического нивелирования состоит в том, что между двумя точками физической поверхности Земли устанавливают нивелир таким образом, чтобы визирная ось его трубы совпадала с касательной к уровенной поверхности, проходящей на высоте горизонта инструмента. После установки инструмента берут отсчёты по рейкам, установленным вертикально в обеих точках. Полученная с одной стоянки нивелира разность отсчётов называется нивелирным превыщением, .

Д ля двух точек значительно удалённых одна от другой и по расстоянию и по высоте, определить эту разность с одной установки нивелира нельзя, поэтому выставляют промежуточные точки и нивелирование производят по частям. Суммированием нивелирных превышений вдоль линии нивелирования от уровня моря – точки О (рис 5.1) до точки В, в которой определяется высота, получают так называемую измеренную высоту

Если перемещения вдоль линии нивелирования, соответствующие , и сами считать бесконечно малыми, то, очевидно, можно написать

Измеренная высота (рис 5.2) складывается из отрезков отвесных линий между уровенными поверхностями, которые пересекают физическую поверхность в точках стояния нивелирных реек вдоль линии нивелирования. Уровенные поверхности, отражающие общую эллипсоидальность Земли и местные неравномерности расположения масс внутри земной коры, не параллельны между собой. Вследствие этого зависит от пути, по которому прокладывалась линия нивелирования. В этом нетрудно убедиться взяв два крайних случая (рис 5.2): 1) нивелирование выполняется от уровня моря (точки О) до точки D, а затем вдоль уровенной поверхности до точки В и 2) нивелирование выполняется от точки О вдоль уровня моря до точки С и затем до точки В. В первом случае измеренная высота будет равна длине отрезка отвесной линии ОD, а во втором случае – отвесной линии СВ. Но так как ОD и СВ вообще не равны, то измеренные высоты точки В, очевидно, будут зависеть от пути проложения нивелирного хода. Различия в результатах нивелирования вследствие разных путей нивелирования в районах равнинных – порядка сантиметров, а в горных районах при длинных ходах могут достигать метров. По этой причине в замкнутых нивелирных ходах, свободных от всех ошибок измерений будут получаться невязки, которые выразятся сумной превышений в замкнутых ходах. В дальнейшем эту невязку будем называть теоретической невязкой.

Для более глубокого выяснения вопроса обратимся к физической стороне проблемы.

В поле силы тяжести Земли элементарная работа на единицу массы или элементарное изменение потенциала силы тяжести определяется произведением ускорения силы тяжести g на элементарное перемещение по высоте . В соответствии с обозначениями рис 5.2 можно записать равенства

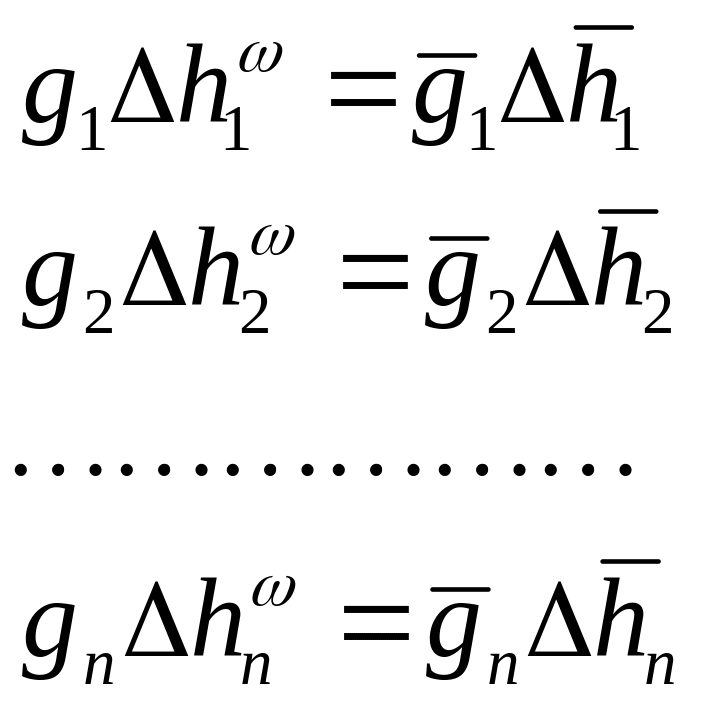
где измеренные ускорения силы тяжести в точках постановки рейки;

ускорения силы тяжести на соответствующих уровенных поверхностях по линии СВ.

Суммируя эти равенства, получим

В пределе

где среднее значение на линии СВ. Отрезок СВ представляет собой расстояние от геоида до физической поверхности Земли, которое называется ортометрической высотой точки В и обозначается обычно через .

Таким образом,

Это строгая формула для ортометрической высоты. Интеграл в формуле выражает разность потенциалов , значение которой не зависит от пути нивелирования. Для точек одной и той же уровенной поверхности ортометрические высоты будут различны, так как различны в различных точках одной и тойже уровенной поверхности. Однако получить ортометрическую высоту по формуле не представляется возможным. Если значение интеграла можно найти сравнительно легко, то величину невозможно определить точно. Для того, чтобы точно вычислить , необходимо знать плотность масс, лежащих между физической поверхностью Земли и геоидом и внутри геоида в каждой точке. Значение можно было бы найти точно в том случае, если по отвесной линии ВС пробурить скважину до геоида и измерить силу тяжести на различных глубинах до поверхности геоида, а затем из измеренных значений силы тяжести взять среднее . Такой способ в реальных условиях, конечно, невозможен и приводится для пояснения физического смысла.

До исследований Ф.Н. Красовского ортометрические высоты вычисляли недопустимо упрощённо, так как принималась во внимание только та часть непараллельности уровенных поверхностей, которая зависит от изменения силы тяжести с широтой. Изменения положения уровенных поверхностей из-за неравномерного распределения масс внутри земной коры считались малыми и не принимались во внимание. Такой метод вычисления высот был следствием того, что силу тяжести вдоль линии нивелирования не измеряли и не оставалось ничего иного, как брать её нормальные значения, вычисленные по аргументам и Н_изм , и исправлять измеренную высоту определяемой точки только за непараллельность уровенных поверхностей нормального потенциала. Исправленную таким образом высоту называют п риближённой. Обозначим приближённую высоту точки В через и определим её в полном соответствии с ортометрической высотой следующим образом:

где среднее значение нормальной силы тяжести по высоте между точками С и В.

нормальное значение силы тяжести в текущей точке линии нивелирования.

Выведем теперь основное выражение для нормальной высоты, которая, как известно, отсчитывается от поверхности квазигеоида.

При выводе уравнения, определяющего возмущающий потенциал на поверхности Земли, было установлено, что значение нормального потенциала на отсчётном эллипсоиде должно быть равно потенциалу реальной Земли в исходном пункте нивелирования. Это значит, что если на отсчётной поверхности нормальный потенциал равен , то на уровенной поверхности, проходящей через футшток в Кронштадте, потенциал силы тяжести реальной Земли . В общем случае (т.е. потенциал силы тяжести на уровне и нормальный потенциал на отсчётной поверхности не совпадают).

Проведём через исследуемую точку В физической поверхности Земли уровенную поверхность, на которой потенциал силы тяжести . Рассмотрим уровенную поверхность нормального потенциала, для которой . Расстояние от уровенной поверхности , проходящей через исследуемую точку В, до уровенной поверхности нормального потенциала есть высота квазигеоида . Откладывая высоты квазигеоида от отсчётной поверхности в соответствующих точках, можем построить таким образом вспомогательную поверхность – квазигеоид. Расстояния от квазигеоида до точки В на поверхности Земли есть нормальная высота. Условимся обозначать её через h. Из самого определения следует

Разность нормальных потенциалов можно представить в виде

где интеграл берётся от отсчётной поверхности (точки С´) вдоль отвесной линии нормального поля, проходящей через точку В до В´;

dh – элементарное расстояние между уровенными поверхностями вдоль линии СВ.

Значение как разность потенциалов можно записать так:

Подставив выражения () и () в формулу будем иметь

В правой части выражения нормальную силу тяжести γ можно заменить на среднее значение нормальной силы тяжести в промежутке от точки С´ до точки В´. Тогда

Эта формула определяет нормальную высоту через разность потенциалов и среднее значение нормальной силы тяжести вдоль отвесной линии нормального потенциала, проходящей через исследуемую точку В. Значение в отличии от , легко и точно вычисляется по формуле приведения в свободном воздухе, т.е.

где значение нормальной силы тяжести, выбираемое из таблиц по широте точки В.

Анализируя формулу (), можно сказать, что нормальные высоты ни в какой мере не зависят от пути нивелирования, в то время как обычная ортометрическая поправка, поскольку она вынуждено вычисляется упрощённо, полностью не снимает зависимости результата нивелирования между двумя фиксированными точками от положения соединяющей их ходовой линии, что, конечно сказывается при замыкании ходов высокоточного нивелирования. И ортометрические и нормальные высоты на одной и той же уровенной поверхности изменяются произвольно в той степени, в какой меняется от точки к точке величина g_m , то нормальные высоты изменяются по строгому закону изменения нормального значения силы тяжести в зависимости от широты.

Этот недостаток ортометрических и, в несколько меньшей степени, нормальных высот, очень досадный при использовании высот при решении инженерных задач, и особенно задач гидротехнического характера, устраняется введением так называемых динамических высот. Сравнивая выражения () и (), легко видеть, что числители их одинаковы и вполне характеризуют положение точки по высоте, так как численная величина интеграла в любой точке одной и той же уровенной поверхности постоянна. Переменными величинами в формулах () и () являются и , и если заменить их на какое-то фиксированное значение силы тяжести, то формулы () и () будут выражением динамической высоты, которая при перемещении точки по уровенной поверхности не изменяется. Обозначая динамическую высоту через h_d и принимая в качестве фиксированного значения нормальной силы тяжести на широте будем иметь

За фиксированное значение силы тяжести не обязательно принимать ; можно взять, например, среднее значение силы тяжести для данного района. Такие высоты также будут обладать всеми свойствами динамических высот. Заметим, что динамические высоты на являются строгими в вопросах, связанных с определением фигуры Земли.