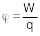Закон гука

Сила упругости прямо пропорциональна величине деформации.

Закон Гука справедлив при малых ( упругих) деформациях тел.

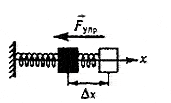
Модуль силы Гука:

F упр = k | x |

где k -коэффициент упругости или жесткость пружины (ед.изм. в СИ - 1 Н/м ) х - удлинение пружины или величина деформации пружины ( ед.изм. в СИ - 1м) Fупр - сила упругости (ед.изм. в СИ - 1Н)

2. Работа сил электростатического поля при перемещении заряда из одной точки поля в другую не зависит от формы траектории, а определяется только положением начальной и конечной точек и величиной заряда.

Аналогичным свойством обладает и гравитационное поле, и в этом нет ничего удивительного, так как гравитационные и кулоновские силы описываются одинаковыми соотношениями.

Следствием независимости работы от формы траектории является следующее утверждение:

Работа сил электростатического поля при перемещении заряда по любой замкнутой траектории равна нулю.

Потенциал поля в данной точке пространства равен работе, которую совершают электрические силы при удалении единичного положительного заряда из данной точки в бесконечность.

Потенциал φ_∞ поля точечного заряда Q на расстоянии r от него относительно бесконечно удаленной точки вычисляется следующим образом:

Потенциал электростатического поля — скалярная величина, равная отношению потен­циальной энергии заряда в поле к этому заряду: - энергетическая характеристика поля в данной точке. Потенциал не зависит от величины заряда, помещенного в это поле.
Т.к. потенциальная энергия зависит от выбора системы координат, то и потенциал определяется с точностью до постоянной. За точку отсчета потенциала выбирают в зависимости от задачи: а) потенциал Земли, б) потенциал бесконечно удаленной точки поля, в) потенциал отрицательной пластины конденсатора.
- следствие принци­па суперпозиции полей (потенциалы складываются алгебраически).
Потенциал численно равен работе поля по перемещению единичного положительного заряда из данной точки электрического поля в бесконечность. В СИ потенциал измеряется в вольтах:
Разность потенциалов
Напряжение — разность значений потенциала в начальной и конечной точках траектории. Напряжение численно равно работе электростатического поля при перемещении единичного положительного заряда вдоль силовых линий этого поля. Разность потенциалов (напряжение) не зависит от выбора системы координат!
Единица разности потенциалов Напряжение равно 1 В, если при перемещении положительного заряда в 1 Кл вдоль силовых линий поле совершает работу в 1 Дж.

Билет 10

Враща́тельное движе́ние — вид механического движения. При вращательном движении абсолютно твёрдого тела его точки описывают окружности, расположенные в параллельных плоскостях. Центры всех окружностей лежат при этом на одной прямой, перпендикулярной к плоскостям окружностей и называемой осью вращения. Ось вращения может располагаться внутри тела и за его пределами. Ось вращения в данной системе отсчёта может быть как подвижной, так и неподвижной. . Основое уравнение динамики вращательного движения материальной точки - угловое ускорение точки при ее вращении вокруг неподвижной оси пропорционально вращающему моменту и обратно пропорционально моменту инерции.

М = E*J или E = M/J

Сравнивая полученное выражение со вторым законом Ньютона с поступательным законом, видим, что момент инерции J является мерой инертности тела вращательного движении.. второй закон Ньютона для вращательного движения

По определению угловое ускорение и тогда это уравнение можно

переписать следующим образом или

(5.10)

Это выражение носит название основного уравнения динамики вращательного движения и формулируется следующим образом: изменение момента количества движения твердого тела , равно импульсу момента всех внешних сил, действующих на это тело.

Это выражение носит название основного уравнения динамики вращательного движения и формулируется следующим образом: изменение момента количества движения твердого тела , равно импульсу момента всех внешних сил, действующих на это тело.

Момент инерции механической системы относительно неподвижной оси a («осевой момент инерции») — физическая величина J_a, равная сумме произведений масс всех n материальных точек системы на квадраты их расстояний до оси:

,

где: m_i — масса i-й точки, r_i — расстояние от i-й точки до оси.

Осевой момент инерции тела J_a является мерой инертности тела во вращательном движении вокруг оси a подобно тому, как масса тела является мерой его инертности в поступательном движении.

• Кинетическая энергия вращательного движения

где I_z — момент инерции тела относительно оси вращения. ω — угловая скорость

Моме́нт и́мпульса (кинетический момент, угловой момент, орбитальный момент, момент количества движения) характеризует количество вращательного движения. Величина, зависящая от того, сколько массы вращается, как она распределена относительно оси вращения и с какой скоростью происходит вращение. Момент импульса частицы относительно некоторого начала отсчёта определяется векторным произведением её радиус-вектора и импульса:

2.Тепловая машина. Устройство, преобразующее энергию теплового движения в механическую энергию, называется тепловой машиной. Различают циклические и нециклические тепловые машины.