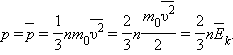Билет16. Поле тяготения. Работа сил тяготения

Изучая притяжение тел по закону всемирного тяготения, мы встречаемся с гравитационным взаимодействием между телами. Это взаимодействие является одним из видов фундаментальных взаимодействий, существующих в природе. Оно осуществляется на расстоянии без непосредственного контакта между взаимодействующими телами.

Согласно представлениям материалистической науки, любое взаимодействие тел на расстоянии осуществляется посредством материальной среды, называемой полем (и поле, и вещество являются формами существования материи).

Гравитационное взаимодействие между телами, описываемое законом всемирного тяготения, осуществляется посредством гравитационного поля (поля тяготения). В каждой точке поля тяготения на помещенное туда тело действует сила тяготения, пропорциональная массе этого тела. Сила тяготения не зависит от среды, в которой находятся тела.

Поле тяготения обладает специфическим свойством, состоящим в том, что при переносе тела массой m из одной точки поля тяготения в другую работа силы тяготения не зависит от траектории движения тела, а зависит только от положения в этом поле начальной и конечной точек перемещения тела. Силы, обладающие подобным свойством, называют консервативными, а поле таких сил - потенциальным. Следовательно, поле тяготения является потенциальным полем, а сила тяготения - консервативной силой.

Расчет показывает, что работа силы тяготения А в поле тяготения Земли определяется по формуле

A=GMm(1/r₁-1/r₂), (2.27)

где m - масса тела; M - масса Земли; r₁ и r₂ - расстояния от центра Земли до начальной и конечной точек перемещения тела.

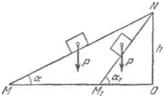
A=Ph (94.1)

Отсюда мы можем сделать и более общий вывод: по какому бы пути ни опускался груз, сила тяжести Р совершает работу А = Рh, где h — высота, на которую опустился груз. Действительно, любой путь мы можем представить себе состоящим из большого числа участков различных наклонных плоскостей (рис. 162). Работа по каждому из участников определяется высотой, на которую опустился груз при перемещении по этому участку. Работа же по всему пути равна действующей на груз силе тяжести, умноженной на полную высоту, на которую опустился груз.

Потенциальная энергия в поле тяготения Земли

Потенциальная энергия в поле тяготения Земли вблизи поверхности приближённо выражается формулой:

О физическом смысле понятия потенциальной энергии

• Если кинетическая энергия может быть определена для одного отдельного тела, то потенциальная энергия всегда характеризует как минимум два тела или положение тела во внешнем поле.

• Кинетическая энергия характеризуется скоростью; потенциальная — взаиморасположением тел.

• Основной физический смысл имеет не само значение потенциальной энергии, а её изменение.

• Потенциальная энергия — скалярная физическая величина, характеризующая способность некоего тела (или материальной точки) совершать работу за счет его нахождения в поле действия сил. Другое определение: потенциальная энергия — это функция координат, являющаяся слагаемым в лагранжиане системы, и описывающая взаимодействие элементов системы

• Потенциальная энергия взаимодействия тела с Землей.

• Найдем работу, совершаемую силой тяжести F_т при перемещении тела массой т вертикально вниз с высоты h₁ над поверхностью Земли до высоты h₂ (рис. 1).

• 

• Рис. 1.

• Если разность h₁ – h₂ пренебрежимо мала по сравнению с расстоянием до центра Земли, то силу тяжести F_т во время движения тела можно считать постоянной и равной mg.

• Так как перемещение совпадает по направлению с вектором силы тяжести, работа силы тяжести равна

• A = F∙s = m∙g∙(h_l – h₂). (5)

• Рассмотрим теперь движение тела по наклонной плоскости. При перемещении тела вниз по наклонной плоскости (рис. 2) сила тяжести F_т = m∙g совершает работу

• A = m∙g∙s∙cos  = m∙g∙h, (6)

• где h – высота наклонной плоскости, s – модуль перемещения, равный длине наклонной плоскости.

• 

• Рис. 2.

• Движение тела из точки В в точку С по любой траектории (рис. 3) можно мысленно представить состоящим из перемещений по участкам наклонных плоскостей с различными высотами h', h" и т. д. Работа А силы тяжести на всем пути из В в С равна сумме работ на отдельных участках пути:

• Физическую величину, равную произведению массы тела на модуль ускорения свободного падения и на высоту, на которую поднято тело над поверхностью Земли, называют потенциальной энергией взаимодействия тела и Земли.

• Работа силы тяжести при перемещении тела массой т из точки, расположенной на высоте h₂, в точку, расположенную на высоте h₁ от поверхности Земли, по любой траектории равна изменению потенциальной энергии взаимодействия тела и Земли, взятому с противоположным знаком.

• А= – (Е_р2 – Е_р1). (9)

• Потенциальная энергия обозначается буквой Е_р.

• Значение потенциальной энергии тела, поднятого над Землей, зависит от выбора нулевого уровня, т. е. высоты, на которой потенциальная энергия принимается равной нулю. Обычно принимают, что потенциальная энергия тела на поверхности Земли равна нулю.

• При таком выборе нулевого уровня потенциальная энергия Е_р тела, находящегося на высоте h над поверхностью Земли, равна произведению массы m тела на модуль ускорения свободного падения g и расстояние h его от поверхности Земли:

• E_p = m∙g∙h.

2. ДИАГРАММА СОСТОЯНИЯ И ФАЗОВЫЕ ПЕРЕХОДЫ I РОДА

Фаза — термодинамически равновесное состояние вещества, отличающееся по физическим свойствам от других возможных равновесных состояний того же вещества. Если, например, в закрытом сосуде находится вода, то эта система является двухфазной: жидкая фаза — вода; газообразная фаза — водяные пары. Если система является однокомпонентной, т. е. состоящей из химически однородного вещества, то понятие фазы совпадает с понятием агрегатного состояния вещества, которое может быть жидким, твердым или газообразным.

Агрегатное состояние вещества зависит от его давления и температуры

ФАЗОВЫЕ ПЕРЕХОДЫ I РОДА Плавление — переход из твердого кристаллического состояния в жидкое. Кристаллизация (затвердевание) — переход вещества из жидкого в кристаллическое (твердое) состояние. Сублимация (возгонка) — переход из твердого кристаллического состояния в газообразное. Конденсация — переход из газообразного состояния в жидкое или твердое. Испарение — переход из жидкого состояния в газообразное. Тепловой эффект фазового перехода I рода рассчитывается по формуле: , где — удельная теплота фазового перехода — количество тепла, поглощаемого или выделяемого при фазовом переходе 1 килограмма вещества, — масса вещества.

Изотермы перехода из жидкого состояния в газообразное Кривая испарения на диаграмме состояния заканчивается в критической точке. Если температура оказывается выше критической, то различие между жидкой и газообразной фазой пропадает, наблюдается явление критической опалесценции.

Билет 17Основное в задачах на эту тему это то, что работа силы упругости при деформации (сжатии или растяжении пружины) всегда отрицательна, так как сила упругости направлена противоположно перемещению конца пружины. При возвращении пружины в положение равновесия (распрямлении) работа силы упругости всегда положительна, так как смещение и сила упругости направлены в одну сторону. Сила упругости зависит от того, насколько деформирована пружина. В процессе деформации она изменяется от нуля до максимального значения. Поэтому работа силы упругости зависит от величины смещения конца пружины, причем нелинейно.

.

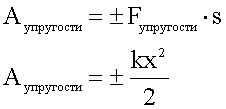
Потенциальнаяэнергия деформированной пружины

Когда мы сжимаемпружину, заводим механические устройства, часы, будильник, мы также запасаемэнергию, как и при подъеме груза и в маятниковых часах. Деформации, сжатие иизгиб тел вызывает силу упругости. Их удобно изучать на пружине или резинке слегко измеримым растяжением. Из формулы силы упругостиF_у=-kx, можно получить формулу еепотенциальной энергии Е_п=A=-F_cpx=-kx²/2, подобноформуле кинетической энергии. Сила упругости пропорциональна деформации,перемещению, и для вычисленияя ее работы можно взять среднее значениеA=F_ys=-k(x₁+x₂)(x₁-x₂)=--½k(x₁²-x₂²)=-∆E_п.

2.изопроцессы в газах

Из уравнения Менделеева - Клапейрона следуют законы, по которым изменяется состояние газов, когда один из параметров – температура, давление или объём остаются неизменным.

В большинстве случаев при переходе газа из одного состояния в другое меняются все его параметры – температура, объём и давление. Так происходит, когда газ сжимается под поршнем в цилиндре двигателя внутреннего сгорания, в результате чего температура газа и его давление растут, а объём уменьшается. Однако в некоторых случаях изменения одного из параметров газа относительно малы или вообще отсутствуют. Такие процессы, где один из трёх параметров – температура, давление или объём остаются неизменными, называют изопроцессами, а законы, которые их описывают – газовыми законами.

И зотермическим процессом называют изменение состояния газа, при котором его температура остаётся постоянной. Этот закон, называемый законом Бойля-Мариотта,

Изобарным процессом называют изменение состояния газа, происходящее при постоянном давлении. Согласно уравнению Менделеева-Клапейрона (24.4) при изобарном процессе отношение объёма данной массы газа к его температуре постоянно. Этот вывод, который называют законом Гей-Люссака :

Процесс, при котором изменяется состояние газа, а его объём остаётся неизменным, называют изохорным. Из уравнения Менделеева - Клапейрона следует, что у газа, занимающего постоянный объём, отношение его давления к температуре тоже должно быть постоянным:

Уравнение (25.3) описывает закон Шарля, Зависимость между давлением и температурой газа при изохорном процессе называют изохорой, которая является прямой

Рис. 25. а, б, в – изотермы, изобары и изохоры идеального газа, соответственно.

Билет 18 В физике механи́ческая эне́ргия описывает сумму потенциальной и кинетической энергии, имеющихся в компонентах механической системы. Механическая энергия — это энергия, связанная с движением объекта или его положением, способность совершать механическую работу

Закон сохранения механической энергии утверждает, что если тело или система подвергается действию только консервативных сил, то полная механическая энергия этого тела или системы остаётся постоянной. В изолированной системе, где действуют только консервативные силы, полная механическая энергия сохраняется.

Полной механической энергией системы тел называется сумма кинетической и потенциальной энергий:

E = E_к + E_п.

Уравнение состояния идеального газа

Уравнение состояния идеального газа (иногда уравнение Клапейрона или уравнение Менделеева — Клапейрона) — формула, устанавливающая зависимость между давлением, молярным объёмом и абсолютной температурой идеального газа. Уравнение имеет вид:

Билет 19 Механическая работа — это физическая величина, являющаяся скалярной количественной мерой действия силы или сил на тело или систему, зависящая от численной величины и направления силы (сил) и от перемещения точки (точек) тела или системы

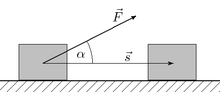
• работа нескольких сил определяется естественным образом как работа их равнодействующей (их векторной суммы). Поэтому дальше в этом параграфе будем говорить об одной силе.

При прямолинейном движении одной материальной точки и постоянном значении приложенной к ней силы работа (этой силы) равна произведению величины проекции вектора силы на направление движения и величины совершённого перемещения^[3]:

Коэффициент полезного действия представляет собой отношение отдаваемой мощности к подводимой мощности.

Потери мощности в электрических машинах. Преобразование механической энергии в электрическую в генераторе и электрической энергии в механическую в двигателе сопровождается некоторыми потерями энергии, которые выделяются в виде тепла, нагревая электрическую машину.

Энергетические диаграммы генератора и двигателя наглядно показывают баланс мощности в этих машинах. Как видно из них, при работе электрической машины возникают потери мощности: электрические, магнитные, механические и добавочные.

Электрические потери ?Р_эл появляются в результате того, что каждая обмотка (в машине постоянного тока обмотки якоря, возбуждения, добавочных полюсов и компенсационная) обладает определенным сопротивлением, препятствующим прохождению по ней электрического тока. Как было показано в § 13, они пропорциональны сопротивлению данной обмотки и квадрату протекающего по ней тока, т. е. сильно возрастают с увеличением нагрузки машины. Электрические потери вызывают нагрев проводов обмоток. К электрическим потерям относятся также потери, возникающие при протекании тока через щетки и через переходное сопротивление между щетками и коллектором; они вызывают нагрев коллектора и щеток.

2. Молекулярно-кинетической теорией называют учение о строении и свойствах вещества на основе представления о существовании атомов и молекул как наименьших частиц химических веществ.

В основе молекулярно-кинетической теории лежат три основных положения:

1. Все вещества – жидкие, твердые и газообразные – образованы из мельчайших частиц – молекул, которые сами состоят из атомов («элементарных молекул»). Молекулы химического вещества могут быть простыми и сложными, т.е. состоять из одного или нескольких атомов. Молекулы и атомы представляют собой электрически нейтральные частицы. При определенных условиях молекулы и атомы могут приобретать дополнительный электрический заряд и превращаться в положительные или отрицательные ионы.

2. Атомы и молекулы находятся в непрерывном хаотическом движении.

3. Частицы взаимодействуют друг с другом силами, имеющими электрическую природу. Гравитационное взаимодействие между частицами пренебрежимо мало.

4. Наиболее ярким экспериментальным подтверждением представлений молекулярно-кинетической теории о беспорядочном движении атомов и молекул является броуновское движение. Это тепловое движение мельчайших микроскопических частиц, взвешенных в жидкости или газе. Оно было открыто английским ботаником Р. Броуном в 1827 г. Броуновские частицы движутся под влиянием беспорядочных ударов молекул. Из-за хаотического теплового движения молекул эти удары никогда не уравновешивают друг друга. В результате скорость броуновской частицы беспорядочно меняется по модулю и направлению, а ее траектория представляет собой сложную зигзагообразную кривую . Теория броуновского движения была создана А. Эйнштейном в 1905 г. Главный вывод теории А. Эйнштейна состоит в том, что квадрат смещения <r²> броуновской частицы от начального положения, усредненный по многим броуновским частицам, пропорционален времени наблюдения t.

<r2> = Dt.

5. Это соотношение выражает так называемый диффузионный закон. Как следует из теории коэффициент пропорциональности D монотонно возрастает с увеличением температуры.

6. Постоянное хаотичное движение молекул вещества проявляется также в другом легко наблюдаемом явлении – диффузии. Диффузией называется явление проникновения двух или нескольких соприкасающихся веществ друг в друга. Наиболее быстро процесс протекает в газе, если он неоднороден по составу. Диффузия приводит к образованию однородной смеси независимо от плотности компонентов. Так, если в двух частях сосуда, разделенных перегородкой, находятся кислород O₂ и водород H₂, то после удаления перегородки начинается процесс взаимопроникновения газов друг в друга, приводящий к образованию взрывоопасной смеси – гремучего газа. Этот процесс идет и в том случае, когда легкий газ (водород) находится в верхней половине сосуда, а более тяжелый (вислород) – в нижней.

7. Значительно медленнее протекают подобные процессы в жидкостях. Взаимопроникновение двух разнородных жидкостей друг в друга, растворение твердых веществ в жидкостях (например, сахара в воде) и образование однородных растворов – примеры диффузионных процессов в жидкостях.

8. В реальных условиях диффузия в жидкостях и газах маскируется более быстрыми процессами перемешивания, например, из-за возникновения конвекционных потоков.

9. Наиболее медленно процесс диффузии протекает в твердых телах. Однако, опыты показывают, что при контакте хорошо очищенных поверхностей двух металлов через длительное время в каждом из них обнаруживается атомы другого металла.

10. Диффузия и броуновское движение – родственные явления. Взаимопроникновение соприкасающихся веществ друг в друга и беспорядочное движение мельчайших частиц, взвешенных в жидкости или газе, происходят вследствие хаотичного теплового движения молекул.

11. Беспорядочное хаотическое движение молекул называется тепловым движением. Кинетическая энергия теплового движения растет с возрастанием

12. Кривая распределения Максвелла позволит найти среднюю арифметическую скорость

13. . Таким образом,

    (11.1)

14. С Повышением температуры наиболее вероятная скорость возрастает, поэтому максимум распределения молекул по скоростям сдвигается в сторону больших скоростей, а его абсолютная величина уменьшается. Следовательно, при нагревании газа доля молекул, обладающих малыми скоростями уменьшается, а доля молекул с большими скоростями увеличивается.

15. Аналитически она выражается формулой

    ,

16. где m – масса молекулы, k – постоянная Больцмана.

Билет 20.

Условия равновесия тел.

Равновесием в механике называют состояние тела, находящегосяв покое (относительно выбранной системы отсчета, обычно Земли). Если телодвижется прямолинейно и равномерно, можно также выбрать систему отсчета, гдеоно неподвижно, покоится.

Состояние покоя называют статичным, а раздел механики о неми условиях равновесия – статикой

Статика включаетновые понятия центров масс, инерции, моментов, оси вращения. Условиемравновесия тела является равенство нулю суммы сил и суммы их моментовотносительно любой оси.

Опыт показывает, что тело покоится, если равнодействующаявсех действующих на него сил равна нулю.

Это записывается в векторном видеF_p=F₁+F₂+…+F_n=0,где равнодействующая сила - векторная сумма всех сил, действующих на тело,равна нулю. Тогда и сумма проекций всех сил налюбое направление равна нулю, например, для оси ОХ,F_1х+F_2х+…+F_nх=0,аналогично для Y, Z. Проекции сил – скалярные величины,просто числа, поэтому с ними решать задачи проще, чем с векторами. Поэтомуважно выбрать более удобный вид, проекцию.

Равновесие бывает устойчивым и неустойчивым.

Это зависит отповедения при отклонении от положения равновесия. В реальных условиях на теладействуют случайные силы, сотрясения, колебания воздуха, окружающей среды. Приэтом тело отклоняется от положения равновесия и силы, действующие на тело,изменяются. Равнодействующая их отличается от нуля и вызывает движение. Еслиэто движение и равнодействующая возвращает тело в положение равновесия, то ононазывается устойчивым. Если же равнодействующая удаляет тело от равновесия, тооно называется неустойчивым.

Примером устойчивого и неустойчивого положения равновесияявляется шар в центре вогнутой и выпуклой подставки, или внизу и вверху сферы

Условие равновесия тела, имеющего ось вращения – это равенство нулю алгебраической суммы моментов приложенных к нему сил. Момент силы – это произведение ее величины на длину рычага – расстояния до точки вращения.

2. Основное уравнение молекулярно-кинетической теории идеальных газов :