Работа 2

ИССЛЕДОВАНИЕ ЛИНЕЙНЫХ КОРРЕКТИРУЮЩИХ КОДОВ

Цель работы - исследование основных свойств линейных корректирующих кодов, методов и устройств их получения (ко­дирования) и декодирования.

Общие сведения

Основные понятия и определения.

Корректирующими называют коды, позволяющие обнару­живать и исправлять ошибки, возникающие при передаче инфор­мации.

При передаче сообщений, представленных в виде последова­тельностей (комбинаций) двоичных символов, кодирование состо­ит в замене К - символьных информационных комбинаций более длинными n - символьными кодовыми комбинациями, передаваемы­ми по каналу связи. Закон, который устанавливает соответствие, между кодовыми и информационными комбинациями, называется пра­вилом кодирования, или кратко кодом. Для совокупности кодо­вых комбинаций важной характеристикой является расстояние Хэмминга между двумя кодовыми комбинациями, то есть количе­ство символов, в которых две кодовые комбинации отличаются друг от друга. Например, между комбинациями

А1 = (1 1 0 1 0) и А2 = (0 1 1 0 0) расстояние Хэмминга d{А1,А2} = 3, так как комбинации содержат три несовпадающих символа (1-й, 3-й и 4-й).

Минимальное из множества расстояний Хэмминга для всего кода называется кодовым расстоянием. Кодовое расстояние яв­ляется важнейшей характеристикой кода, так как определяет его корректирующую способность, то есть способность кода обнаруживать и исправлять ошибки заданной кратности, под которой понимают число искаженных символов. Связь между ко­довым расстоянием d0 и кратностью обнаруживаемых (qобн) или исправляемых (qиспр) ошибок устанавливается следующими соотношениями.

При обнаружении ошибок d0 = qобн + 1

При исправлении ошибок d0 = 2qиспр + 1

При одновременном исправлении, ошибок до кратности qиспр обнаружении ошибок более высокой кратности

d0 = qиспр+qобн + 1

Циклические коды.

Математической основой построения циклических кодов яв­ляется сопоставление n - символьным кодовым комбинациям не­которых полиномов степени n – 1. Причем, символы комбинации являются коэффициентами этих полиномов. Например, комбинации (1 0 0 1 0 1) можно сопоставить полином y(t) = 1*t⁵ + 0*t⁴ + 0*t³ + 1*t² + 0*t¹ + 1*t⁰ = t⁵ + t² + 1, у которого коэффициентами при пе­ременной t являются символы комбинации. Для множества та­ких полиномов вводятся операции сложения, вычитания, умножения и деления, совпадающие с обычными операциями над полино­мами, с той лишь разницей, что сложение коэффициентов полино­мов производится по модулю 2. При этом операции сложения и вычитания совпадают, так как из равенства I I = 0 следует, что I = -I. Алгоритм деления, например, полинома t⁵ + t³ + 1

на полином t³ + t² + 1 выглядит следующим образом:

t⁵ + 0*t⁴ + t³ + 0*t² + 0*t + 1 t³ + t² + 0*t + 1

t² + t

t⁵ + t⁴ + 0*t³ + t²

t⁴ + t³ + t² + 0*t

t⁴ + t³ +0*t² + t

t² + t + 1

В результате деления получился полином частного t² +t и остаток от деления R(t) = t² +t + 1. Так как операции над полиномами сводятся к операциям над коэффициентами при t, являющимися символами двоичных последовательностей, то при выполнении, операций переменную t можно опустить. При этом запись алгоритма деления упрощается и для рассмотренно­го примера имеет вид

1 0 1 0 0 1 1 1 0 1

1 1 0 => t² + t

1 1 0 1

1 1 1 0

1 1 0 1

0 1 1 1

0 0 0 0

1 1 1 => R(t) = t² + t + 1

По полученным двоичным комбинациям определяется полином част­ного t² + t и остатка

R(t) = t² + t + 1

Основное свойство циклических кодов состоит в том, что по­лином степени n - 1, соответствующий n -символьной комбина­ции циклического кода, делится без остатка на некоторый поли­ном g(t) степени r = n – k, называемый порождающим, то есть

Y(t) = g(t) l(t)

где l(t) - полином степени k - 1.

Порождающий полином полностью определяет вею совокупность полиномов, соответствующих комбинациям кода (порождает код).

Для того чтобы полином g(t) степени r порождал код, он должен быть делителем двучлена tⁿ + 1, то есть

tⁿ + 1 = g(t) h(t)

где h(t) - полином степени k.

Из указанного свойства порождающего полинома следует, что его свободный член равен 1. Для того чтобы порождаемый поли­ном g(t) код имел кодовое расстояние d0 , количество отличных от нуля коэффициентов g(t) должно быть не менее d0, так как комбинация, соответствующая g(t) также принадлежит коду.

Рассмотрим работу регистра при поступлении на вход информационной комбинации

(1 1 0 1).

Значения сигналов и состояния регистра приведены в табл. 2.2.

Таблица 2.2

№ такта	Вход	Состояние регистра в конце такта			COС	Коман­да ко­дирования	Выход кодера
		T1	T2	T3
I	1	1	1	0	1	1	1
2	1	1	0	1	1	1	1
3	0	1	0	0	1	1	0
4	1	1	0	0	1	1	1
5	0	0	1	0	0	0	0
6	0	0	0	1	0	0	0
7	0	0	0	0	0	0	1

До поступления входных сигналов триггеры регистра находились в состоянии 0.

В тече­ние первого такта входной сигнал (I) складывается с нулевым значением третьего триггера, в результате чего значение сиг­нала обратной связи равно 1. Этот сигнал записывается к кон­цу такта в триггер TI и после сложения с нулевым значением триггера

TI – в триггер Т2. В триггер ТЗ перепишется нулевое значение из Т2. Во втором такте входной сигнал (1) складыва­ется с сигналом ТЗ (0), в результате чего CОС равен 1. Этот сигнал к концу такта запишется в Т1. В триггер Т2 запишется результат сложения COС (I) и значения TI в предыдущем такте (l), то есть 0, а в ТЗ перепишется содержимое Т2 (I). Анало­гично будут протекать процессы в третьем и четвертом тактах. К концу четвертого такта в регистре будет записано состояние I 0 0, соответствующее полиному остатка

R(t)= 1.

По существу, в регистре оказываются записанными значения избыточных симво­лов кодовой комбинации. Для получения всей кодовой комбинации надо обеспечить поступление избыточных символов после инфор­мационных.

Циклическое декодирование.

Схема циклического декодера для кода (7,4) содержит (рис.2.6) приемный 7-разрядный (в общем случае n - разрядный) ре­гистр сдвига, регистр g(t) для получения остатка, схему И, выполняющую функцию дешифратора одной комбинации остатка (1 0 0), сумматор по модулю 2 для последовательного исправ­ления принятой комбинации, схему "Запрет" для отключения об­ратной связи в регистре g(t) и переключатель режима рабо­ты S.

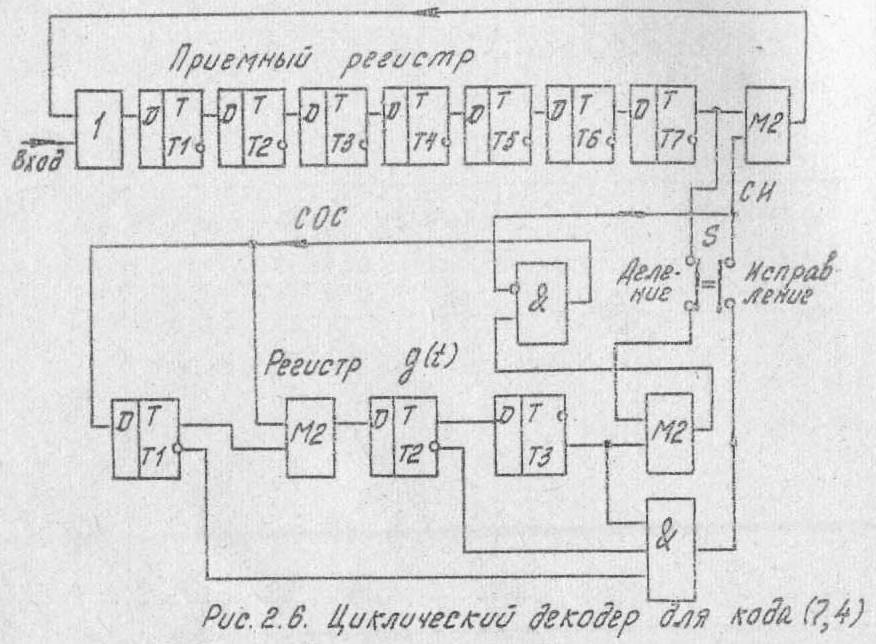
Декодирование производится в два этапа. На первом этапе переключатель S ставится в положение “Деление” и в течение 7 тактов принятая комбинация подается в регистр g(t), где к концу 7-го такта получается остаток. Одновре­менно принятая комбинация подается на вход приемного регист­ра через схему ИЛИ, то есть производится ее циклический сдвиг, так что к концу 7-го такта она снова оказывается записанной в регистре, причем в триггере Т7 записано значение a₁’ (В реальных условиях этап деления может быть совмещена с прие­мом кодовой комбинации из канала связи).

На втором этапе (переключатель S- в положении “Исправление^”) производится циклический сдвиг комбинации, в приемном регистре и коэффициентов в регистре g(t) .

В момент, когда искаженный символ поступает на сумматор по модулю 2, с выхода регистра g(t) на схему и подаются сигналы 0 0 1, и значение сигна­ла исправления равно 1. Благодаря этому, искаженный символ изменяется на противоположный и его правильное значение запи­сывается в триггер TI приемного регистра. Одновременно сигнал исправления разрывает цепь обратной связи в регистре g(t) (с помощью схемы "Запрет") и в нем устанавливается нулевое состо­яние. Весь процесс исправления производится в течение 7 так­тов.

В качестве примера в табл. 2.4 приведены значения сиг­налов в различных ,точках декодера при приеме комбинаций (1 1 0 1 0 0 0), у которой искажен третий избыточный символ (отмечен точкой).

Из таблицы видно, что к концу этапа деления (7-й такт) в регистре g(t) устанавливается состояние I I 0, соответству­ющее остатку при искажении 4 (см.табл.2.3). На этапе исправления по мере перемещения искаженного символа в приемном регистре (отмечен точкой) изменяется и состояние регистра g(t) таким образом, что комбинации коэффициентов остатка в регистре g(t) однозначно связаны с номером искаженного символа в приемном регистре в соответствии с табл.2.3. К концу 13-го такт искаженный символ записывается в триггер T7, а в регистре g(t) устанавливается состояние 0 0 1.

При этом значение сигнала исправления на выходе схемы И становится равным I.

В следующем такте искаженный символ и сигнал исправления, равный I, подается на выходной сумматор. Происхо­дит исправление искаженного символа, так что к концу послед­ него такта в приемном регистре оказывается исправленная комбинация, а в регистре g(t) устанавливается нулевое состояние.

Таблица 2.4

Номер такта	Вход регистра	Состояние регистра g(t)			СОС	Сигнал исправ-ления	Состояние приемного регистра							Выход декодера	Этап
		T1	T2	T3			T1	T2	T3	T4	T5	T6	T7
1	1	1	1	0	1	0	1	0*	0	0	1	0	1	1	Деление
2	1	1	0	1	1	0	1	1	0*	0	0	1	0	1
3	0	1	0	0	1	0	0	1	1	0*	0	0	1	0
4	1	1	0	0	1	0	1	0	1	1	0*	0	0	1
5	0	0	1	0	0	0	0	1	0	1	1	0*	0	0
6	0	0	0	1	0	0	0	0	1	0	1	1	0*	0
7	0*	1	1	0	1	0	0*	0	0	1	0	1	1	0*
8	0	0	1	1	0	0	1	0*	0	0	1	0	1	1	Исправление
9	0	1	1	1	1	0	1	1	0*	0	0	1	0	1
10	0	1	0	1	1	0	0	1	1	0*	0	0	1	0
11	0	1	0	0	1	0	1	0	1	1	0*	0	0	1
12	0	0	1	0	0	0	0	1	0	1	1	0*	0	0
13	0	0	0	1	0	1	0	0	1	0	1	1	0*	0
14	0	0	0	0	0	0	1	0	0	1	0	1	1	1