2.2.3. Устойчивые и неустойчивые звенья второго порядка

2.2.3.1. Общие положения

Элемент экономической системы может иметь динамические процессы, имеющие ярко выраженный колебательный характер. В этом случае переходные динамические процессы могут быть отражены в виде решения дифференциального уравнения второго порядка. Звено, динамические свойства которого отражаются дифференциальным уравнением вида:

(2.15)

называют колебательным звеном второго порядка.

Преобразуем по Лапласу это уравнение:

а₀ · p² · Y(p) + a₁ · p · Y(p) + a₂ · Y(p) = b · X(p) , (2.16)

или, иначе:

(a₀ · p² + a₁ · p + a₂) · Y(p) = b · X(p). (2.17)

Определим передаточную функцию звена:

. (2.18)

Если записать уравнение (2.16) без входного воздействия (нулевые входные воздействия X(p) = 0) и сократить Y(p), то получим:

(2.19)

Такое уравнение называется характеристическим, поскольку характеризует исключительно внутренние свойства звена. В записи звена содержатся три параметра:

(2.20) где T — постоянная времени (в годах);

η — коэффициент затухания колебаний (безразмерная величина);

k — передаточный коэффициент.

Корни характеристического уравнения (2.19) определяются по формуле:

. (2.21)

Вид корней характеристического уравнения (вещественные, комплексно-сопряженные или чисто мнимые) определяется величиной дискриминанта уравнения. В данном случае он равен:

(2.22)

При D ≥0 переходные процессы в динамических звеньях будут носить монотонный характер, а при D <0 – колебательный характер. График функции D = f(η), приведенный на рисунке 2.4., наглядно показывает области A и F монотонных переходных процессов, расположенных над осью абсцисс и области B, C и E колебательных переходных процессов, расположенных под осью абсцисс.

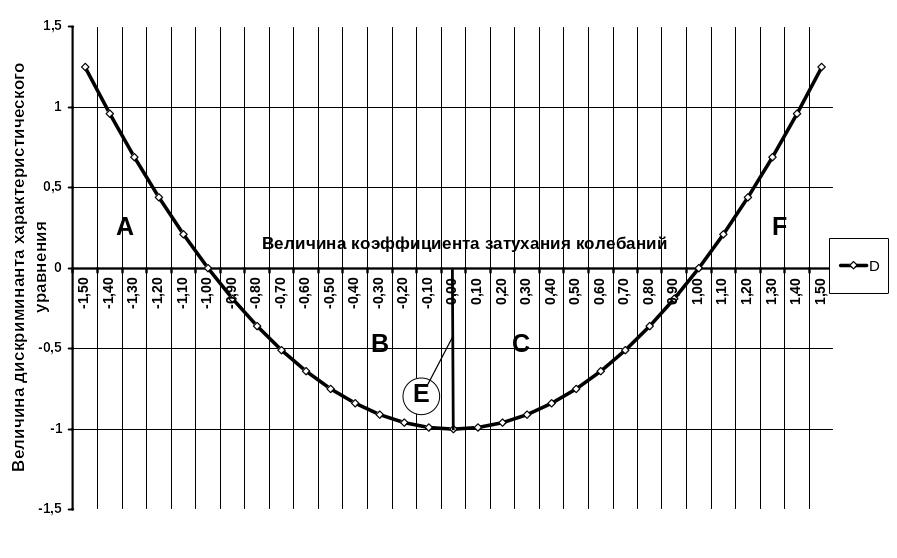
Рисунок 2.4. График зависимости величины дискриминанта характеристического уравнения от коэффициента затухания колебаний

Такой подход носит универсальный характер. Например, для моделей делового цикла Самуэльсона-Хикса и Тевеса подобным образом построены графики для D = 0, в координатах: предельная склонность к потреблению и акселератор инвестиций. Данные графики использованы для объяснения характера переходных процессов в национальной экономике при различных сочетаниях значений акселератора инвестиций и предельной склонности к потреблению.

В зависимости от величины коэффициента затухания колебаний η звенья второго порядка классифицируются по видам:

η ≥ 1 — устойчивое апериодическое звено второго порядка (область F);

η ≤ - 1 — неустойчивое апериодическое звено второго порядка (область A);

0 < η < 1 — устойчивое колебательное звено второго порядка (область C);

0 > η > -1 — неустойчивое колебательное звено второго порядка (область B);

η = 0 — консервативное звено второго порядка (область E).

Рассмотрим более подробно динамические свойства каждого звена второго порядка.