§1.5. Ускорение

Третья кинематическая характеристика - ускорение - характеризует быстроту изменения скорости. Рассмотрим понятие ускорения для материальной точки. На рис. 4 показаны два положения на траектории д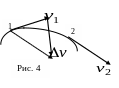 вижущейся частицы, соответствующие им скорости и , и приращение скорости . Вектор среднего ускорения

< > = (1.5.1)

Мгновенное ускорение:

(1.5.2)

При прямолинейном движении вектор ускорения совпадает с вектором скорости при ускоренном движении и противоположен ему при замедленном. При движении по криволинейной траектории (см. рис. 4) вектор ускорения направлен под углом к вектору скорости внутрь траектории. Всякий вектор имеет две характеристики – модуль и направление, они могут изменяться независимо друг от друга. При криволинейном движении скорость может изменяться как по величине, так и по направлению, поэтому удобно рассматривать две составляющие вектора ускорения. Используя формулы (1.4.3) и (1.4.4), получаем:

(1.5.3)

Вектор ускорения состоит из двух слагаемых – тангенциального и нормального ускорений. Первая составляющая – тангенциальное ускорение характеризует быстроту изменения вектора скорости по величине. При убыстрении движения и направлены в одну сторону, при замедлении они противоположны. Величина тангенциального ускорения

a_= (1.5.4)

Вторая составляющая – нормальное ускорение связано с изменением направления скорости. Это хорошо известное из школьного курса физики центростремительное ускорение при равномерном движении тела по окружности. Оно направлено по радиусу к центру окружности и равно:

(1.5.5)

R – радиус кривизны траектории, т.е. радиус соприкасающейся окружности, дугой которой можно заменить бесконечно малый участок кривой в окрестности данной точки. Задав в этой точке орт нормали , направленный по радиусу окружности в ее центр, получаем:

(1.5.6)

Н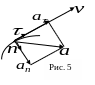 а рис 5 показан небольшой участок траектории, где в данный момент времени находится движущаяся частица. Орты касательный и нормали взаимно перпендикулярны, соответственно, перпендикулярны друг другу тангенциальное и нормальное ускорения, и полное ускорение равно:

(1.5.7)

Если закон движения задан в координатной форме, то модуль ускорения можно вычислить аналогично модулю скорости (см. формулу 1.4.7) так:

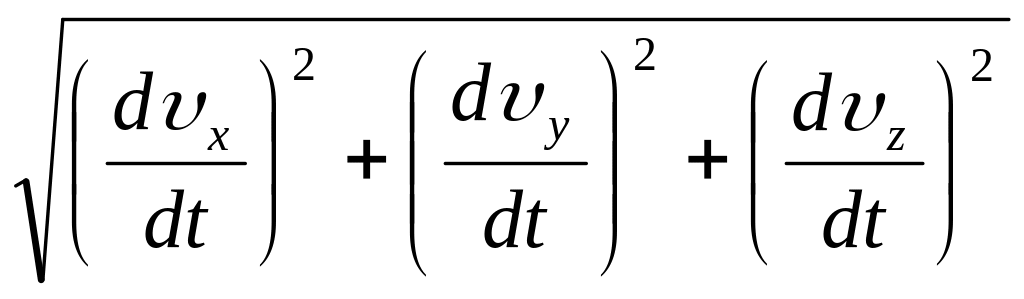= (1.5.8)

Проекции вектора ускорения на оси координат соответственно:

, , (1.5.9)

При вращении тела быстроту изменения его угловой скорости указывает угловое ускорение . Его среднее значение

<> =  /t (1.5.9)

Мгновенное угловое ускорение

, (1.5.10)

и - аксиальные (осевые) векторы. Направление вектора угловой скорости определяет правило правого винта. При ускоренном вращении векторы и направлены по оси вращения в одну сторону, при замедленном – в противоположные стороны. В СИ угловая координата измеряется в радианах (рад), угловая скорость в рад/с, угловое ускорение в рад/с².