§ 7.2. Закон Био-Савара-Лапласа

1. Этот закон позволяет рассчитать магнитное поле, созданное тонким произвольной формы проводником с током. Лаплас теоретически обобщил результаты экспериментального изучения Био и Саваром магнитного поля вокруг проводников с током (1820 г.). На рис.45 представлен отрезок криволинейного проводника, направление тока в нем указано стрелкой. Выделим элемент длины проводника dl. Элементом тока называется вектор , он направлен по касательной к проводнику в данной точке. Элементарное магнитное поле, созданное этим элементом тока в некоторой точке пространства (ее положение относительно элемента тока задает вектор ), выражает закон Био-Савара-Лапласа:

(7.2.1)

Вектор направлен перпендикулярно векторам и по правилу векторного произведения, т.е.по касательной к изображенной на рис. 27 окружности. Его модуль

(7.2.2)

Магнитное поле, созданное всеми элементами тока проводника, найдем по принципу суперпозиции:

(7.2.3)

Рассмотрим примеры расчета магнитного поля тока.

2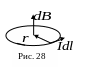 . Поле в центре кругового тока (рис.28). По тонкому проводнику, имеющему форму окружности радиуса r, течет постоянный ток I. Векторы и взаимно перпендикулярны, первый направлен по касательной к окружности, второй – по радиусу в центр. Векторы всех элементов тока направлены вдоль оси окружности, так что . Кружок на интеграле означает, что перемещение образует замкнутый контур длиной 2r. Магнитная индукция в центре кругового витка с током

(7.2.4)

Отметим, что направление вектора магнитной индукции в центре кругового т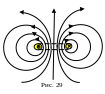 ока и направление тока в витке связаны правилом правого винта.

Подобным образом можно рассчитать магнитное поле в любой точке. На рис. 29 показано сечение витка плоскостью, в которой лежит его ось. Желтые кружки обозначают сечение проводника с током, крестик и точка указывают направление тока в нем. Магнитное поле изображено силовыми линиями, стрелками указано их направление. Обратите внимание, что силовые линии магнитного поля всегда замкнуты. Силовая линия, совпадающая с осью витка, замыкается на бесконечности, остальные за пределами границ рисунка.

3. Поле прямолинейного тока (рис. 30). Вектор перпендикулярен плоскости прямоугольного треугольника, гипотенуза которого равна r и катет b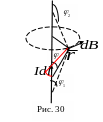 =rsin противолежит углу . направлен по касательной к окружности радиуса b с центром на проводнике с током. Его величина . Найдем магнитное поле, которое в указанной на рисунке точке создает отрезок проводника, заданный углами ₁ и ₂. Выразим dl и r через . При перемещении по проводнику на dl получается новый треугольник (его гипотенуза нарисована красной линией), угол увеличится на d. Новое положение гипотенузы получается поворотом отрезка r на такой центральный угол. Учитывая малость d, получаем, что проекция на проводник дуги окружности r d равна dl= rd/sin. Заметим, что все элементы прямолинейного тока создают в этой точке одинаково направленные векторы магнитной индукции, так что

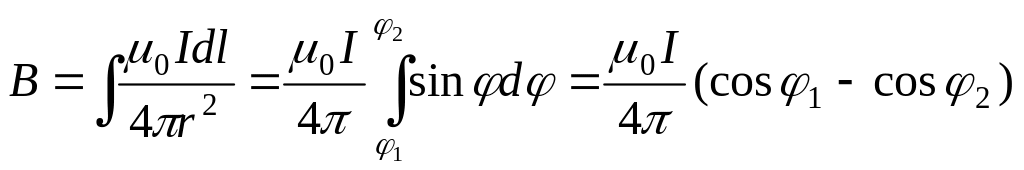(7.2.5)

Для бесконечно длинного проводника ₁=0, ₂=, так что

(7.2.6)

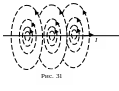З аметим, что силовые линии магнитного поля прямолинейного тока являются концентрическими окружностями, их плоскости перпендикулярны проводнику с током, а центры лежат на проводнике. На рис. 31 показан отрезок бесконечно длинного прямолинейного проводника с током, лежащего в плоскости рисунка. Его силовые линии – концентрические окружности – в плоскости рисунка изображены овалами. Правые половинки овалов соответствуют частям окружностей перед плоскостью рисунка, левые - за плоскостью рисунка. Направление силовых линий связано с направлением тока в проводнике правилом правого винта. Густота силовых линий уменьшается при удалении от проводника