Три пекарни осуществляют ежедневные поставки хлеба для четырех магазинов. Ниже представлена информация о спросе на продукцию, ее наличии и транспортных издержках.
Пекарня
|
Транспортные издержки, пенсов/m |
Общее предложение |
|||
Магазин |
|||||
I |
II |
III |
IV |
||
Х |
1,5 |
2,5 |
1,0 |
2,0 |
700 |
Y |
2,0 |
3,0 |
2,0 |
1,5 |
650 |
Z |
1,0 |
1,5 |
2,5 |
3,0 |
800 |
Общая потребность |
400 |
500 |
350 |
1000 |
|
Определить является модель сбалансированной или несбалансированной.
Найти план перевозок, при котором затраты на транспортировку будут минимальны.
Администрация деревоперерабатывающего предприятия "Vibra" приняла на работу пять человек. Каждый из них имеет различные способности и навыки и затрачивает различное время на выполнение определенной работы. В настоящее время необходимо выполнить пять видов работ. Время выполнения работы каждым работником приведено в таблице:
Работник |
Время выполнения, ч |
||||
Работы 1 |
Работы 2 |
Работы 3 |
Работы 4 |
Работы 5 |
|
Ml М2 МЗ М4 М5 |
25 25 30 27 29 |
16 17 15 20 19 |
15 18 20 22 17 |
14 23 19 25 32 |
13 15 14 12 10 |
Требуется назначить на каждый вид работы одного из работников. Как это нужно сделать, чтобы общее время, необходимое для завершения всех видов работ, было минимальным?
Компания, занимающаяся добычей железной руды, имеет 4 карьера (С), производительность которых соответственно равна: 170, 150, 190 и 200 тыс.т. ежемесячно. Железная руда направляется на 3 принадлежащие этой компании обогатительный фабрики (S), мощности которых соответственно 250, 150, 270 тыс.т в месяц. Транспортные расходы (в тыс. руб.) на перевозку 1 тыс. руды с карьеров на фабрики:
-
S1
S2
S3
C1
7
3
8
C2
5
4
6
C3
4
5
9
C4
6
2
5
Определить является модель сбалансированной или несбалансированной.
Найти план перевозок, при котором затраты на транспортировку будут минимальны.
Для транспортной задачи, исходные данные которой приведены в таблице
|
Пункты отправления |
||||
80 |
120 |
160 |
120 |
||
Пункты назначения |
120 |
1 |
3 |
4 |
2 |
160 |
4 |
5 |
8 |
3 |
|
200 |
2 |
3 |
6 |
7 |
|
Определить является модель сбалансированной или несбалансированной.
Найти план перевозок, при котором затраты на транспортировку будут минимальны.
Для транспортной задачи, исходные данные которой приведены в таблице
|
Пункты отправления |
||||
60 |
60 |
20 |
10 |
||
Пункты назначения |
10 |
10 |
20 |
5 |
7 |
20 |
13 |
9 |
12 |
8 |
|
30 |
4 |
15 |
7 |
9 |
|
40 |
14 |
7 |
1 |
0 |
|
50 |
3 |
12 |
5 |
19 |
|
Определить является модель сбалансированной или несбалансированной.
Найти план перевозок, при котором затраты на транспортировку будут минимальны.
Для транспортной задачи, исходные данные которой приведены в таблице
|
Пункты отправления |
|||
5 |
10 |
15 |
||
Пункты назначения |
20 |
5 |
1 |
0 |
10 |
3 |
2 |
4 |
|
15 |
7 |
5 |
2 |
|
15 |
9 |
6 |
0 |
|
Определить является модель сбалансированной или несбалансированной.
Найти план перевозок, при котором затраты на транспортировку будут минимальны.
Для транспортной задачи, исходные данные которой приведены в таблице
|
Пункты отправления |
||||
100 |
130 |
210 |
140 |
||
Пункты назначения |
130 |
4 |
5 |
1 |
2 |
180 |
3 |
6 |
3 |
3 |
|
240 |
5 |
2 |
7 |
1 |
|
Определить является модель сбалансированной или несбалансированной.
Найти план перевозок, при котором затраты на транспортировку будут минимальны.
Для транспортной задачи, исходные данные которой приведены в таблице
|
Пункты отправления |
|||||
10 |
35 |
15 |
25 |
55 |
||
Пункты назначения |
30 |
3 |
7 |
1 |
5 |
9 |
5 |
7 |
5 |
8 |
6 |
3 |
|
45 |
6 |
4 |
8 |
3 |
2 |
|
40 |
3 |
1 |
7 |
4 |
3 |
|
Определить является модель сбалансированной или несбалансированной.
Найти план перевозок, при котором затраты на транспортировку будут минимальны.
Решить задачу линейного программирования.
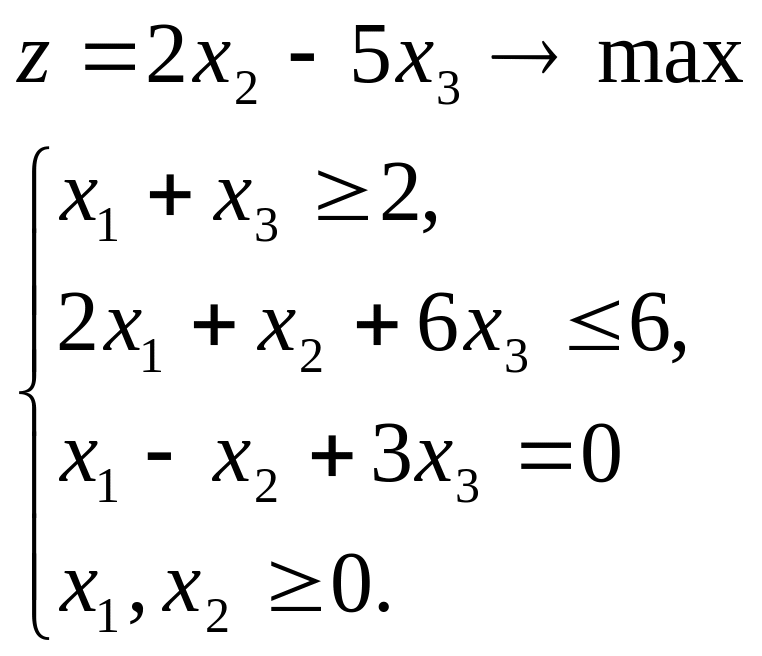
Цех мебельного комбината выпускает трельяжи, трюмо и тумбочки под телевизоры. Норма расхода материала в расчете на одно изделие, плановая себестоимость, оптовая цена предприятия, плановый (месячный) ассортимент и трудоемкость единицы продукции приведены в таблице 4. Запас древесно-стружечных плит, досок еловых и березовых – 90, 30 и 14 м2. Плановой фонд рабочего времени составляет 16800 человеко-часов.
Исходя из необходимости выполнения плана по ассортименту и возможности его перевыполнения по отдельном (или даже всем) показателям, построить модель, на основе которой можно решить а) задачу максимизации объема реализации (за плановой период); б) задачу максимизации прибыли (за тот же период).
Показатели |
Трельяжи |
Трюмо |
Тумбочки |
Норма расхода материала, м2 |
|
||
Древесностружечные плиты |
0,032 |
0,031 |
0,038 |
Доски: еловые |
0,020 |
0,020 |
0,008 |
березовые |
0,005 |
0,005 |
0,006 |
Трудоемкость, чел.-ч. |
10,2 |
7.5 |
5.8 |
Плановая себестоимость |
88,81 |
63,98 |
29,60 |
Оптовая цена предприятия |
93,00 |
76,00 |
30,00 |
Плановой ассортимент |
350 |
290 |
1200 |
На заводе ежемесячно скапливается около 14 т отходов металла, из которого можно штамповать большие и малые шайбы. Месячная потребность завода в больших шайбах 600 тыс. шт., в малых – 1100 тыс. шт. (недостающее количество шайб закупается на специализированном предприятии). Оптовая цена больших шайб 11,9 ед. (за тысячу штук) и малых – 5, 2 ед. Расход металла на тысячу больших шайб – 22 кг, на тысячу малых – 8 кг. Для изготовления шайб используются два пресса холодной штамповки. Производительность каждого за смену составляет 9 тыс. шт. больших шайб либо 11,5 тыс. шт. малых. Завод работает в две смены. Построить модель, на основе которой можно сформулировать экстремальную задачу определения плана производства шайб (из отходов завода), обеспечивающего максимальную долю в валовой продукции предприятия. За плановый период принять год.
Фабрика выпускает кожаные брюки, куртки и пальто специального назначения в ассортименте, заданном соотношением 2:1:3. В процессе изготовления изделия проходят три производственных участка – дубильный, раскройный и пошивочный. Фабрика имеет практически неограниченную сырьевую базу, однако сложная технология предъявляет высокие требования к квалификации рабочих. Численность их в рамках планируемого периода ограничена. Время обработки изделий на каждом участке, их плановая себестоимость, оптовая цена предприятия приведены в таблице.
Показатели |
Брюки |
Куртки |
Пальто |
Норма времени на участках, чел.-ч. |
|
||
Дубильном |
0,3 |
0,4 |
0,6 |
Раскройном |
0,4 |
0,4 |
0,7 |
Пошивочном |
0,5 |
0,4 |
0,8 |
Полная себестоимость |
15 |
40,5 |
97,8 |
Оптовая цена предприятия |
17,5 |
42 |
100 |
Ограничения на фонд времени для дубильного, раскройного и пошивочного участков составляют соответственно 3360, 2688 и 5040 часов.
Учитывая заданной ассортимент, построить модель, на основе которой можно сформулировать экстремальную задачу определения напряженного месячного плана по прибыли от реализованной продукции.