§3.2.2. Идеальные тепловые двухполюсники

В тепловых технических системах происходит перенос и накопление тепловой энергии. При этом потенциальной фазовой характеристикой принято считать температуру T (разность температур ), потоковой фазовой характеристикой – тепловой поток Ф.

В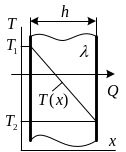 нимание! Тепловой поток – это не тепловая энергия, а скорость передачи тепловой энергии. Для стационарного потока тепловая энергия .

Термическое сопротивление теплопроводности. Простейшим типовым элементом тепловой системы является плоская стенка толщиной h с теплопроводностью материала . Разность температур вызывает тепловой поток Ф.

Примем . Тогда распределение температур по толщине стенки будет линейным. В соответствии с законом Фурье плотность теплового потока составляет . Для получения теплового потока умножим обе части уравнений на площадь S поперечного сечения выделенного участка . Таким образом, математической моделью плоской стенки, переносящей тепловую энергию, является линейное уравнение .

Так как данное уравнение напоминает закон Ома (потенциальная характеристика пропорциональна потоковой), то коэффициент назван термическим или кондукционным сопротивлением плоской стенки. Термическое сопротивление определяется исключительно внутренними параметрами стенки.

О чень часто элементы конструкции тепловых систем выполняются в виде криволинейных поверхностей: отрезков трубы, части сферы. Математической моделью цилиндрической и сферической стенки, переносящей тепловую энергию, также является линейное уравнение . Для части цилиндрической стенки, показанной на рисунке, термическое сопротивление рассчитывается по формуле . Для части сферической стенки, видимой под телесным углом , термическое сопротивление может быть рассчитано по формуле .

Если стенка многослойная, то её термическое сопротивление определяется как сумма термических сопротивлений всех слоёв. В случае неидеального теплового контакта между слоями в эту сумму включаются контактные термические сопротивления.

Термическое сопротивление теплоотдачи. Теплоотдача – это следствие конвективного теплообмена твёрдого тела с окружающей его жидкой или газообразной средой. Для стационарного конвективного теплообмена считают справедливым уравнение Ньютона или , где - коэффициент теплоотдачи, - температура окружающей среды, - температура тела. Математической моделью конвективного теплообмена является линейное уравнение где названо термическим или конвекционным сопротивлением.

Теплоёмкость. Количество тепловой энергии, запасаемой материальным телом удельной теплоёмкостью , массой m, при изменении температуры от начального значения до конечного значения определяется по формуле . Взяв производную по времени, перейдём от энергии к потоку , или , где - теплоёмкость тела. Таким образом, математической моделью теплоёмкости является дифференциальное уравнение первого порядка .

Тепловая индуктивность. В том случае, когда фазовыми переменными являются тепловой поток и температура, компонентное уравнение, соответствующее тепловой индуктивности, не имеет физического смысла.

Идеальным источником теплового потенциала является источник температуры и идеальным источником теплового потока .

Таким образом, тепловая подсистема характеризуется 4 идеальными двухполюсниками, которые, по аналогии с электротехникой, можно представлять схематически следующим образом

.
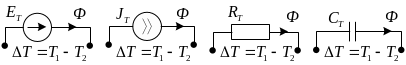