2. Многофакторный корреляционно-регрессионный анализ

Включим в модель переменные Х₅ Х₆ Х₇ Х₉ Х₁₇. Построим многофакторную линейную регрессионную модель для анализа влияния вариации факторных признаков Х₅ Х₆ Х₇ Х₉ Х₁₇ на результативный признак .

Выявление и удаление выбросов проводятся аналогично описанному процессу для случая однофакторной регрессии.

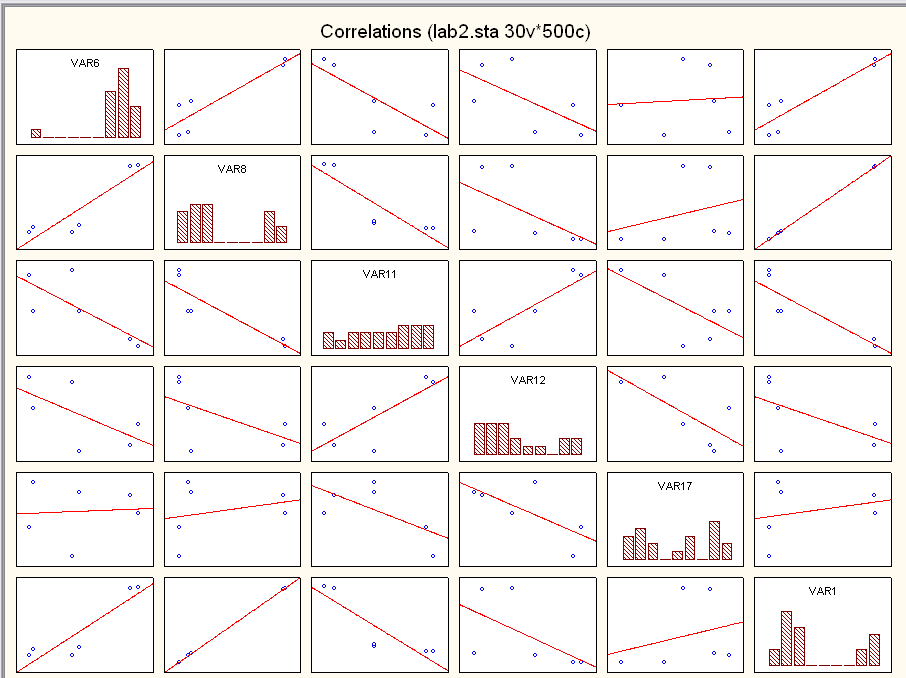
Рис. «Поле корреляции и гистограммы переменных , Х₅ Х₆ Х₇ Х₉ Х₁₇»

Корреляционная матрица содержит коэффициенты корреляции как между факторными и результирующей переменной, так и между самими факторными переменными.

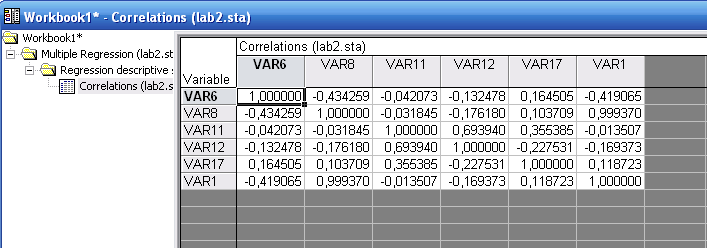
Рис. «Корреляционная матрица»

Корреляционная матрица показывает, что значение коэффициента парной корреляции между переменными и равно -0,419, т.е. направление связи – обратное, связь слабая.

Х₅ и =-0,434259, направление связи – обратное, связь слабая.

Х₆и =-0,042073, направление связи – обратное, связь слабая.

Х₇и =-0,132478, направление связи – обратное, связь слабая.

Х₉и =0,164505, направление связи – обратное, связь слабая.

В случае построения многофакторной модели требуется проверить факторы на мультиколлинеарность. В нашем примере коэффициент корреляции между факторами (равный -0,434259) меньше коэффициентов корреляции факторов с результирующей переменной (соответственно -0,042073 и 0,031845), т.е. мультиколлинеарность отсутствует.

Определим значения параметров b₀, b₁ ,b_2, b₃, b₄ ,b_5, уравнения многофакторной линейной корреляционной связи вида ŷ=b₀+b₁x+ b₂x+ b₃x+ b₄x+ b₅x.

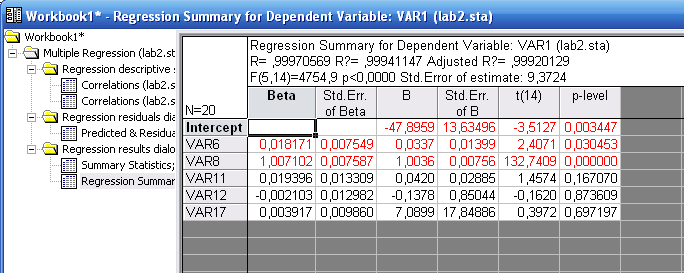
Рис. «Окно Regression Summary for dependent variable – Итоговая таблица регрессии зависимой переменной»

В нашем примере b₀= -47,8959 b₁= 0,0337, b₂= 1,0036,

b₃= 0,0420, b₄= -0,1378, b₅= 7,0899, уравнение регрессии имеет вид:

=-47,8959 +0,0337 Х₅+1,0036 Х₆+0,0420 Х₇-0,1378 Х₉+7,0899 Х₁₇

Совокупный коэффициент множественной детерминации, равный 0,99920129, показывает, что 99,9% вариации показателя объясняется влиянием факторов, включенных в уравнение множественной регрессии (Х₅ Х₆ Х₇ Х₉ Х₁₇).

Проверка адекватности уравнения, значимости найденных коэффициентов регрессии, построение прогноза осуществляются так же, как при проведении однофакторного корреляционно-регрессионного анализа.

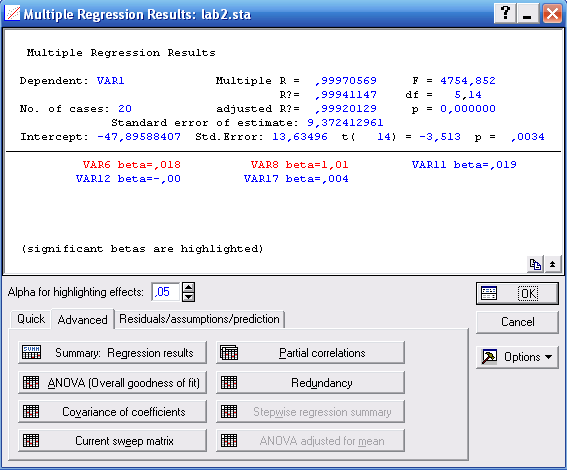
Рис. «Окно результатов корреляционно-регрессионного анализа»

Значимость множественного коэффициента корреляции проверяется по таблице F-критерия Фишера. В нашем случае табличное значение F-критерия Фишера для степеней свободы ν₁=1, ν₂=18 (20 наблюдений минус 2 равно 18) при уровне значимости α=0,05 равно 4,41, а рассчитанное значение равно 4754,852. Расчетное значение больше табличного, поэтому найденный коэффициент парной корреляции имеет высокую значимость между переменными , Х₅ Х₆ Х₇ Х₉ Х₁₇. Как правило F_расч > F_табл минимум в 4 раза.

Нажатие по кнопке Graph – График в диалоговом окне Review Descriptive statistics – Просмотр описательных статистических характеристик откроет график «поле корреляции» исследуемых переменных, а также соответствующие гистограммы.

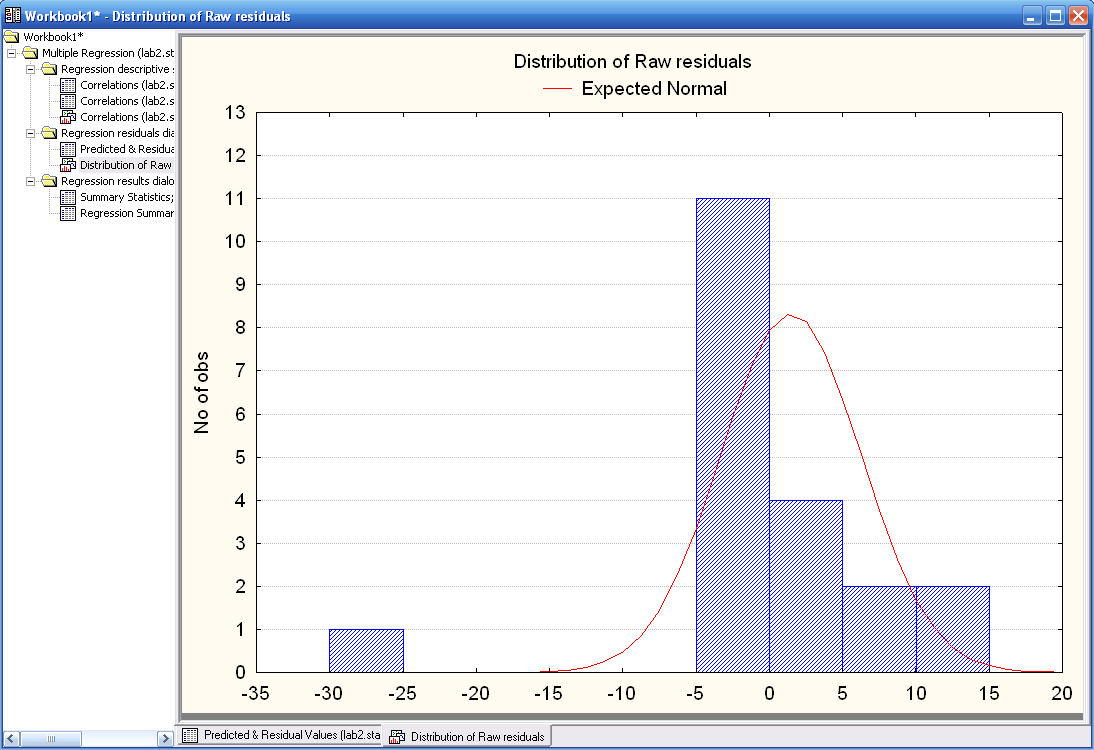
Рис. «График распределения остатков»