Выполнение работы

1) Построим однофакторную регрессионную модель для анализа влияния вариации факторного признака X8 на результативный признак Y3.

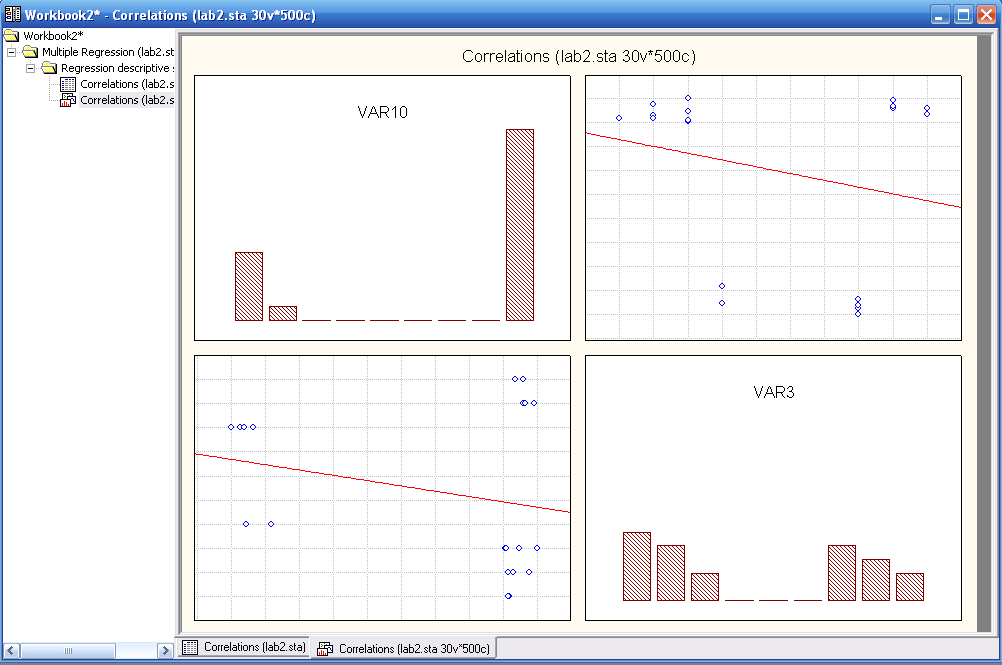
Рис. «Поле корреляции и гистограммы переменных» Х₈ и У₁ .

Для удаления выбросов используют средство Brushing – Кисть, меню которого активизируется кнопкой на панели инструментов.

В группе опций Action – Действия установим маркер на действие Label и, подведя курсор-лупу к предполагаемому «выбросу» на графике поля корреляции, щелкнем левой кнопкой мыши. Соответствующая точка-«выброс» будет выделена. Далее нажмем кнопку Update-Обновить для определения порядкового номера случая-«выброса». Над точкой появился номер: Case 4- Наблюдение 4. Для удаления «выброса» с графика поля корреляции установим маркер на действие Turn OFF-Отключить и нажмем Update-Обновить. Аналогичным образом удалим оставшиеся выбросы. Направление аппроксимирующей функции изменилось, теперь все точки лежат в непосредственной ее близости. Можно сделать вывод о сильном влиянии выброса на результат анализа, удалить выбросы из исходных данных и заново рассчитать коэффициент парной корреляции.

Нажатием кнопки Quit – Выход закончим использование инструмента Brushing – Кисть. Удалим выброс и из исходных данных, предварительно закрыв диалоговое окно Review Descriptive statistics – Просмотр описательных статистических характеристик. Далее снова вызовем Startup Panel – Стартовую панель в меню Analysis-Анализ и проведем расчет коэффициента парной корреляции.

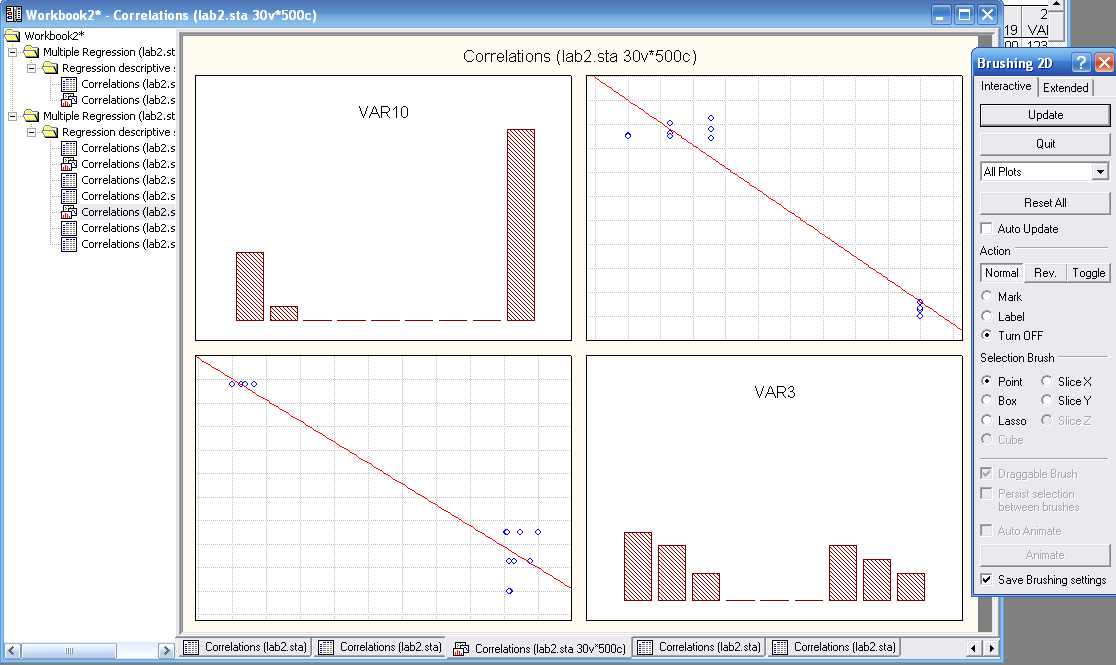
Рис. «Использование инструмента Brushing – Кисть»

Заново рассчитанный коэффициент парной корреляции равен 0,25, что свидетельствует о возможном наличии прямой связи между рассматриваемыми переменными. Принимая гипотезу о прямолинейной форме зависимости между признаками, определим значения параметров b₀ и b₁ уравнения однофакторной линейной корреляционной связи вида ŷ=b₀+b₁x.

Из диалогового окна Review Descriptive statistics – Просмотр описательных статистических характеристик, щелчком на кнопке ОК переходим в диалоговое окно Model Definition – Определение модели, а из него щелчком на кнопке ОК – в окно результатов корреляционно-регрессионного анализа.

По данным нашего примера коэффициент детерминации получился равным 0,06242348, таким образом, 6,2% вариации показателя Х₈ объясняется вариацией показателя .

Значимость множественного коэффициента корреляции проверяется по таблице F-критерия Фишера. В нашем случае табличное значение F-критерия Фишера для степеней свободы ν₁=1, ν₂=18 (20 наблюдений минус 2 равно 18) при уровне значимости α=0,05 равно 4,41, а рассчитанное значение равно 1,198433. Расчетное значение меньше табличного, поэтому найденный коэффициента парной корреляции имеет малую значимость между переменными Х₈ и . Как правило F_расч > F_табл минимум в 4 раза.

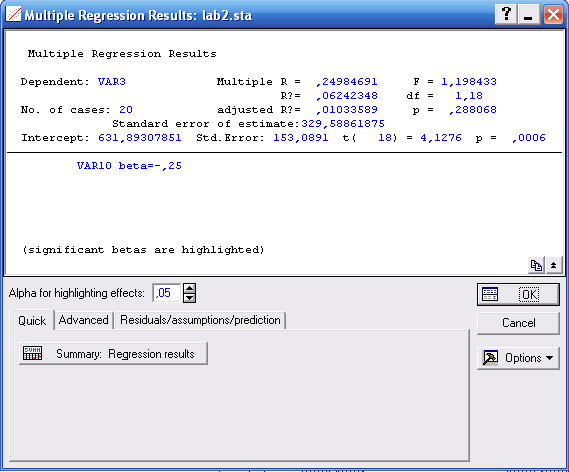
Рис. «Окно результатов корреляционно-регрессионного анализа»

Щелчок по кнопке Regression Summary –Итоговая таблица регрессии в окне результатов регрессионного анализа открывает Regression Summary for dependent variable – Итоговую таблицу регрессии зависимой переменной.

Рис. «Окно Regression Summary for dependent variable – Итоговая таблица регрессии зависимой переменной»

Здесь в столбце B отражены искомые значения параметров b₀ и b₁ регрессионного уравнения. Итак, наше уравнение имеет вид:

=631,8931-0,2119* Х₈

Значимость найденных параметров b₀ и b₁ проверяется по таблице t-критерия Стьюдента. Расчетные значения t-критерия Стьюдента для каждого параметра, отраженные в столбце t(18), сравниваем с табличным значением t-критерия для числа степеней свобода, равного 18. t_табл = 2,101 при уровне значимости α=0,05. Рассчитанные значения t-критерия для первого параметра больше табличного, для второго – меньше.