
- •Лекция 11. Выбор частоты дискретизации сигналов.
- •Амплитудные характеристики кодеков и шумы квантования
- •Защищенность сигнала от шума квантования
- •Лекция 13. Равномерное и неравномерное квантование. Шумы квантования
- •Лекция 14. Принцип работы линейного кодека.
- •Декодер
- •Лекция 15. Дельта-модуляция
- • На выходе схемы вычитания получается разность кодированных отсчетов, т.Е. Сигнал с дикм
- •Лекция 16. Собственные помехи при квантовании группового сигнала
- •Лекция 17. Расчёт количества разрядов в кодовой комбинации. Расчёт защищённости от шумов квантования.
- •Получаем код: 1 1 1 1 0 1 0
- •Лекция 18. Выбор типа линейного кода цсп
- •Лекция 20. Разработка структурной схемы цсп
Лекция 17. Расчёт количества разрядов в кодовой комбинации. Расчёт защищённости от шумов квантования.
В цифровых системах связи определяющим является шум квантования. Шум квантования обусловлен конечностью числа уровней отсчетов и, как следствие, неточностью представления мгновенного уровня сигнала. Разность между исходным и квантованным сигналом называется шумом квантования. Амплитудная характеристика квантующего устройства может быть представлена как сумма идеальной линейной характеристики и ступенчатой функции, определяющей искажения сигнала. Конечность числа уровней квантования определяет максимальную амплитуду входного сигнала. Превышение максимальной амплитуды входного сигнала приводит к ограничению уровня квантованного сигнала (перегрузка кодера). При равномерном шаге квантования шум квантования не зависит от уровня сигнала, поэтому для получения приемлемого соотношения сигнал/шум при малом уровне сигнала необходимо уменьшать шаг, что ведет либо к увеличению числа уровней, либо к ограничению максимальной амплитуды сигнала. Выбор характеристики квантования основан на особенностях восприятия человеческого слуха, чувствительного не к абсолютному уровню шума, а к соотношению сигнал/шум. Это дает возможность увеличивать шаг квантования при увеличении уровня сигнала и за счет этого добиться большего соотношения сигнал/шум при том же числе уровней и динамическом диапазоне. Возможны разные пути неравномерного квантования:
сжатие динамического диапазона сигнала перед квантованием и расширение после обратного преобразования – компандер
применение нелинейной шкалы квантования
В связи с трудностью обеспечения стабильности аналогового сжатия и расширения сигнала, второй способ является предпочтительным.
Поскольку разница
между уровнями сигнала и шума (защищенность
от шума квантования) величина
логарифмическая, все реализации
компрессии имеют характеристику, близкую
к логарифмической. Наибольшее
распространение получила 16-сегментная
шкала квантования с характеристикой
компрессии, соответствующей А-закону.
В этом случае весь динамический диапазон
делят на 16 сегментов, по восемь для
каждой полярности. В пределах каждого
сегмента шаг квантования неизменен.
Для сигналов, абсолютная величина
которых не превышает
![]() ,
шаг квантования равномерный, в дальнейшем
шаг удваивается
,
шаг квантования равномерный, в дальнейшем
шаг удваивается
в каждом следующем сегменте.
![]() о
о шибка
шибка
![]() ∆7
∆7
![]() ∆6
∆6
![]() ∆5
∆5
![]() ∆4
∆4
![]() ∆3
∆3
![]() ∆2
∆2
![]() ∆1
∆1
![]() ∆0
∆0
+∆/2
-∆/2
Ошибка квантования
![]() ,
,
∆1 = ∆2 = … ∆i – равномерная шкала квантования.
![]()
![]() ;
;
![]() .
.
Напомним, что
качество передачи сигнала будет
приемлемым, если
![]() dB.
Для выполнения данного условия, учитывая,
что динамический диапазон телефонного
сигнала 54…66 dB, необходимо
использовать около 2000 уровней квантования,
т.е. 11-разрядный двоичный код (
dB.
Для выполнения данного условия, учитывая,
что динамический диапазон телефонного
сигнала 54…66 dB, необходимо
использовать около 2000 уровней квантования,
т.е. 11-разрядный двоичный код (![]() ).
По этому применяют неравномерное
квантование, при котором число разрядов
кода уменьшается. В современных ЦСП
применяют неравномерное квантование
с амплитудной характеристикой квантующего
устройства сигналов АИМ-2, близкой к
логарифмической. Эта амплитудная
характеристика является линейно-ломанной,
основанной на 16-сегментной аппроксимации.
).
По этому применяют неравномерное
квантование, при котором число разрядов
кода уменьшается. В современных ЦСП
применяют неравномерное квантование
с амплитудной характеристикой квантующего
устройства сигналов АИМ-2, близкой к
логарифмической. Эта амплитудная
характеристика является линейно-ломанной,
основанной на 16-сегментной аппроксимации.
Сегменты
![]() ,
,
![]() ,
,
![]() ,
,
![]() имеют одинаковый наклон, следовательно,
их считают единичным сегментом,
следовательно, характеристика компрессора
получается 13-сегментной. В пределах
каждого сегмента размещается 16 шагов
квантования
имеют одинаковый наклон, следовательно,
их считают единичным сегментом,
следовательно, характеристика компрессора
получается 13-сегментной. В пределах
каждого сегмента размещается 16 шагов
квантования
![]() (к = 0,1,…,15). При 8-разрядном нелинейном
кодировании первый разряд несёт
информацию о полярности отсчёта входного
сигнала. Следующие три разряда кода
образуют номер сегмента (
(к = 0,1,…,15). При 8-разрядном нелинейном
кодировании первый разряд несёт
информацию о полярности отсчёта входного
сигнала. Следующие три разряда кода
образуют номер сегмента (![]() =
0, 1, 2,…,7), а последние четыре разряда –
образуют номер шага квантования (
=
0, 1, 2,…,7), а последние четыре разряда –
образуют номер шага квантования (![]() =
0, 1,…,15) в пределах сегмента.
=
0, 1,…,15) в пределах сегмента.
![]() уровней
квантования
уровней
квантования
 ∆ – шаг
квантования логарифмическая
шкала
∆ – шаг
квантования логарифмическая
шкала

![]()
128
![]()
![]()
![]() 112
112
![]()
96
80
![]()
![]()
64
Центральный
![]()
сегмент 48
 32
32
![]()
![]()
16
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
-16
![]()
![]() -32
-32
-48
![]()
![]() -64
-64
-80
![]()
-96
![]() -112
-112
![]() -128
-128
- текущее мгновенное напряжение входного сигнала
Шаг квантования меняется при переходе от сегмента к сегменту, и определяется:
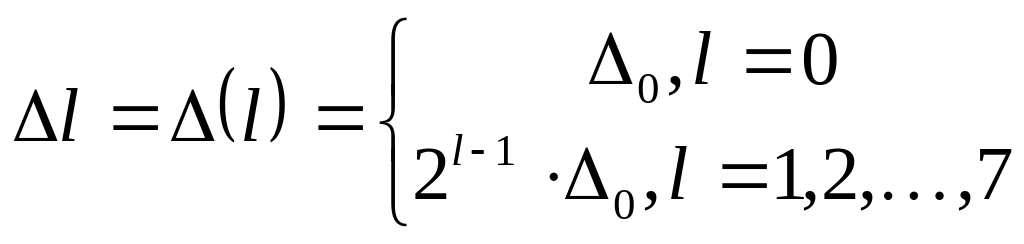
где:
![]() – шаг квантования на центральном
сегменте.
– шаг квантования на центральном
сегменте.
![]() – порог ограничения
кодера.
– порог ограничения
кодера.
Амплитудная
характеристика![]() реализуется в виде каскадного соединения
компрессора с этой характеристикой, с
последовательным включением АЦП с
равномерной шкалой квантования и
компаратором с порогом
.
реализуется в виде каскадного соединения
компрессора с этой характеристикой, с
последовательным включением АЦП с
равномерной шкалой квантования и
компаратором с порогом
.

Максимально допустимая величина защищенности от шумов квантования для данной амплитудной характеристики определяется:
![]() (1)
(1)
где: m – число разрядов в кодовой группе
![]() – выигрыш в
защищённости от шумов квантования при
использовании компандеров
(компрессор – экспандер).
– выигрыш в
защищённости от шумов квантования при
использовании компандеров
(компрессор – экспандер).
С – коэффициент компандирования.
![]() ;
;
![]() - нормированное
- нормированное
![]()
![]() ;
;
![]() - нормированное
- нормированное
![]()
![]() – угол наклона
первого сегмента
– угол наклона
первого сегмента
![]() – угол наклона
последнего сегмента характеристики
квант. устройства.
– угол наклона
последнего сегмента характеристики
квант. устройства.
Наибольшее распространение получила характеристика компрессии типа А-87.6/13, где аппроксимация производится по логарифмическому А-закону компандирования:

А = 87.6 – параметр компрессии.
Защищённость от шумов квантования в зависимости от уровня входного сигнала представлена ниже на рисунке.
Величина для 13-сегментной характеристики компандирования = 24 dB, а коэффициент компрессии С = 36 dB.
Тогда:
![]() .
.
Реальная величина
![]() должна быть снижена на 3…4 дБ. Кроме
того, из-за ошибок АЦП
должна быть снижена ещё на 2…3 дБ.
Следовательно:
должна быть снижена на 3…4 дБ. Кроме
того, из-за ошибок АЦП
должна быть снижена ещё на 2…3 дБ.
Следовательно:
![]() ,
дБ (2)
,
дБ (2)


 40
40
![]() ,
dB
m=8
,
dB
m=8
35



 30
32.2
Норма для 8- разрядной
30
32.2
Норма для 8- разрядной
27.6 m=7 кодовой группы

 25
25
20
 15
15
12.6 3
 10
10
-60 -50
-40 -30 -20 -10 0
![]() ,
dB
,
dB
В ЦСП может быть
n-переприёмов
по ТЧ. Поэтому
на выходе любого из каналов будет меньше,
чем в (2). В каждом пункте переприёма
вносятся шумы из-за АЦП. Но т.к. эти шумы
не коррелированны, следовательно, они
суммируются по мощности и образуют
величину
![]() ,
n
– число переприёмов. Отсюда следует:
,
n
– число переприёмов. Отсюда следует:
![]() ,
дБ (3)
,
дБ (3)
Т.к. задаётся нормами на параметры ТЧ, то зная можно найти требуемое число разрядов кодовой группы (минимально допустимое):
![]() (4)
(4)
6.
![]()
По формуле (3)
определяем минимальную защищенность
сигнала для динамического диапазона
![]() =
-36 дБ. Предполагаем, что :
=
-36 дБ. Предполагаем, что :![]() =
0дБ;
=
0дБ;
![]() =
-36дБ
=
-36дБ
Следовательно:
![]() дБ
дБ
![]() дБ
дБ
Т.к. m
= 7, один разряд – знак. Следовательно
мы имеем
![]() уровня квантования.
уровня квантования.
Здесь лежат значения ,дБ
 25 (
25 (![]() )
)
21 (![]() )
)
= 23 дБ 20
m=7
n=2 15
=40 дБ
10
линейное изменение
(насколько убывает сигнал, то -50 -40 -30 -20 -10 0 +5
н
астолько
убывает
)
-36
дБ (![]() от
)
от
)
![]() дБ
дБ
![]()
До тех пор пока
![]() –
амплитуда входного сигнала не превышает
–
амплитуда входного сигнала не превышает
![]() ,
квантование остаётся равномерным.
Следовательно,
изменяется линейно с изменением уровня
сигнала
(при
,
квантование остаётся равномерным.
Следовательно,
изменяется линейно с изменением уровня
сигнала
(при![]() ,
т.е.
,
т.е.
![]() ).
Максимальная защищённость достигается
при
).
Максимальная защищённость достигается
при
![]() дБ.
При
дБ.
При
![]() дБ
защищённость
меняется незначительно, т.к. при увеличении
уровня сигнала растут и искажения
квантования (за счёт увеличения шага).
дБ
защищённость
меняется незначительно, т.к. при увеличении
уровня сигнала растут и искажения
квантования (за счёт увеличения шага).
При (т.е. достигаем ) наступает перегрузка кодера и защищённость резко падает. Колебательный характер от обусловлен скачкообразным изменением размера шага квантования при переходе от сегмента к сегменту.
 Начальный
участок характеристики компрессора
Начальный
участок характеристики компрессора
0 1/64 1/32 1/16
Характеристика квантования.
Таблица 1.1.
Номер сегмента. |
Размер шага квантования. |
Верхняя граница сегмента |
7 |
64 |
|
6 |
32 |
/2 |
5 |
16 |
/4 |
4 |
8 |
/8 |
3 |
4 |
/16 |
2 |
2 |
/32 |
1 |
|
/64 |
0 |
|
/128 |
Определяем количество разрядов в кодовом слове по формуле 4 [1]:
![]() ,
,
где
![]() –
количество переприемов по ТЧ;
–
количество переприемов по ТЧ;
![]() дБ
– защищенность от шума квантования.
дБ
– защищенность от шума квантования.
![]()
Определяем по
формуле 3 [1] минимальную величину
защищённости сигнала в пункте приёма
в диапазоне уровней
![]() с
учётом заданного числа переприёмов по
ТЧ и аппаратурных погрешностей.
с
учётом заданного числа переприёмов по
ТЧ и аппаратурных погрешностей.
![]() дБ
дБ
Максимальная величина защищённости в том же диапазоне будет примерно на 3дБ больше минимальной.
![]() дБ
дБ
Наносим на график
горизонтальные прямые, соответствующие
найденным
![]() и
и
![]() (рисунок 1.2). Значения защищённости от
искажений квантования в диапазоне
лежат между этими прямыми. Защищённость
при
(рисунок 1.2). Значения защищённости от
искажений квантования в диапазоне
лежат между этими прямыми. Защищённость
при
![]() примерно на
примерно на
![]() дБ
выше
дБ
выше
![]() .
.![]() дБ
дБ
В диапазоне
![]() квантование является равномерным, т.е.
квантование является равномерным, т.е.
![]() убывает равномерно на
убывает равномерно на
![]() дБ
при уменьшении уровня сигнала на такую
же величину. Диапазон изменения уровня
сигнала, в котором защищённость остаётся
не ниже заданной, находим непосредственно
из рисунка. При
дБ
при уменьшении уровня сигнала на такую
же величину. Диапазон изменения уровня
сигнала, в котором защищённость остаётся
не ниже заданной, находим непосредственно
из рисунка. При
![]() дБ,
он составляет
дБ,
он составляет
![]() дБ.
дБ.

Процесс кодирования.
8 – сегментная характеристика компрессии.
![]() № сегм
№ сегм
 8
8
7
0,75 6
5
0,5 4
3
0,15 2
1
0,25
0,5 0,75
![]()
![]() -
знак, m = 7,
-
знак, m = 7,
![]() =
64
=
64
№ сегмента |
Этап кодирования |
Код сегмента |
Нижняя граница сегмента |
Эталонные значения шагов квантования |
||||||
1 |
2 |
3 |
Q2 |
Q3 |
Q4 |
Q5 |
Q6 |
Q7 |
||
|
|
|
|
1 |
1 |
1 |
512 |
64 |
128 |
256 |
7 |
|
|
|
1 |
1 |
0 |
256 |
32 |
64 |
128 |
|
|
|
|
1 |
0 |
1 |
128 |
16 |
32 |
64 |
|
|
|
|
1 |
0 |
0 |
64 |
8 |
16 |
32 |
|
|
|
|
0 |
1 |
1 |
32 |
4 |
8 |
16 |
3 |
|
|
|
0 |
1 |
0 |
16 |
2 |
4 |
8 |
|
|
|
|
0 |
0 |
1 |
8 |
1 |
2 |
4 |
1 |
|
|
|
0 |
0 |
0 |
0 |
1 |
2 |
4 |
7.
![]() =
651
=
1(знак)
=
651
=
1(знак)
6
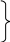 51>
51> (=
64)
(=
64)
 =
1
=
1651>
 (=
256)
(=
256)
 =
1 номер сегмента
=
1 номер сегмента651>
 (=
512)
(=
512)
 =
1
=
1 =
-
=
651-512 = 139
Квантованная разность
=
-
=
651-512 = 139
Квантованная разность
Сравниваем с наибольшим эталонным сигналом:
139 < 256
 =
0
=
0139 > 128
 =
1, следовательно
=
1, следовательно
 =
139 – 128 =11.
=
139 – 128 =11.1

 1
< 64
1
< 64
 =0
=0



 8
8


 6
6 5
5

 4
4
 2
2