4. Метод динамического программирования.

4.1. Принцип оптимальности

Рассмотрим систему

(4.1)

и функционал

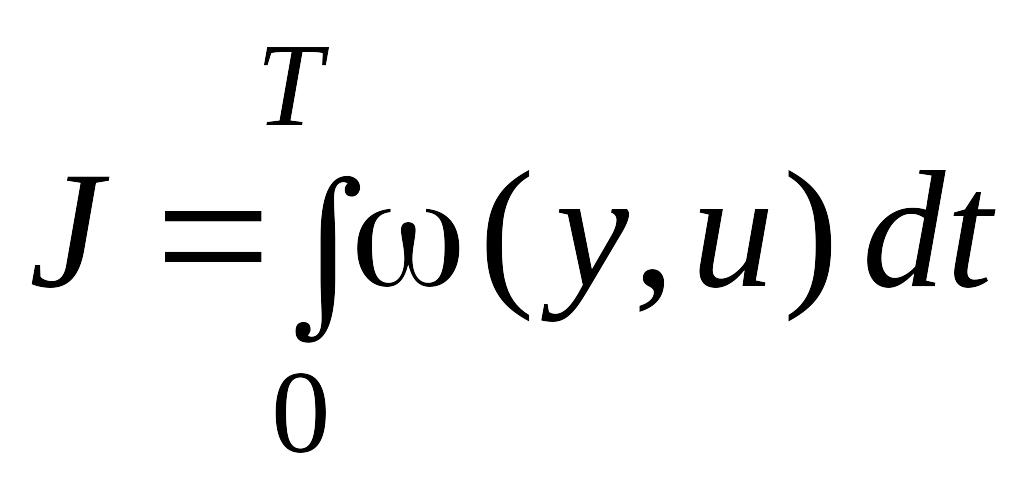(4.2)

который требуется минимизировать. Правый конец фазовых координат является свободным.

Наряду с этой вариационной задачей рассмотрим вспомогательную, когда процесс рассматривается в интервале и минимизируется функционал

. (4.3)

Пусть сначала найден минимум J (4.2) и соответствующее ему оптимальное управление (рис. 1а):

(4.4)

а потом – минимум (4.3) и оптимальное управление (рис. 1б):

. (4.5)

В последнем случае предполагается, что в момент процесс начинается с состояния , достигнутого к моменту времени при оптимизации процесса в интервале .

Вообще говоря, управления и отличаются интервалом и значениями. Принцип оптимальности утверждает, что оптимальные управления и в общей части интервала совпадают, не зависимо от предыстории процесса и вполне определяются состоянием в момент .

В случае со свободным правым концом принцип оптимальности доказывается. В самом деле, допустим, что на участке управления и не совпадают и

. (4.6)

Рис. 1а Рис.1б

Тогда для первой задачи введем управление

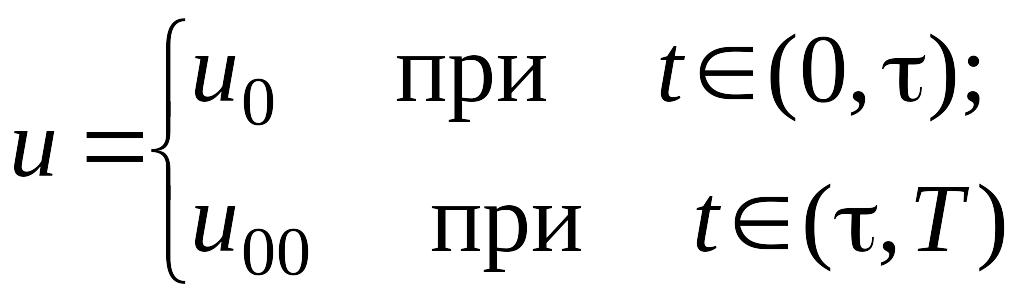(4.7)

и вычислим функционал

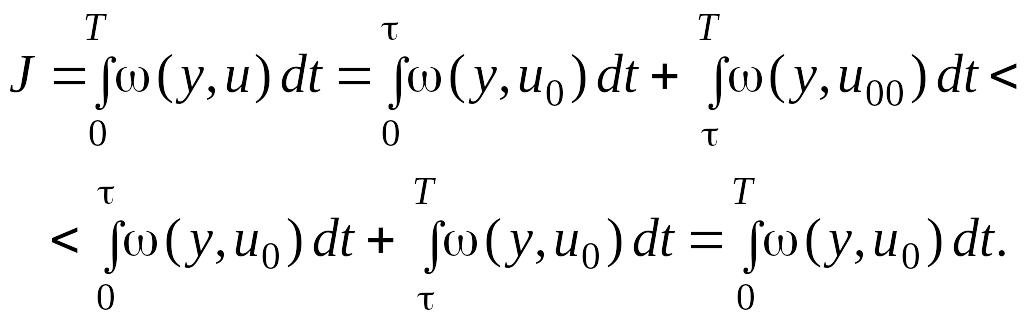
При управлении u (4.7) функционал (4.2) принимает меньшее значение, чем при (4.4). Но управление является оптимальным. Поэтому допущение (4.6) неверно.

A предположение

противоречит тому, что - управление, минимизирующее (4.3).

Таким образом, остается, что

,

и если оптимальное управление единственное, то

.

Кратко принцип оптимальности можно сформулировать так: последний участок оптимальной траектории является оптимальным независимо от предыстории процесса.

4.2. Основное уравнение метода динамического программирования

Применим принцип оптимальности к решению вариационной задачи (4.1), (4.2). Для этого сначала рассмотрим функционал (4.3). Наименьшее значение его при связях (4.1) обозначим:

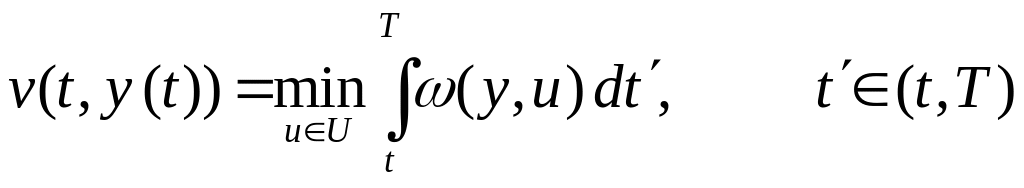. (4.8)

Если - оптимальное управление,

то .

Оптимальное управление зависит от начального состояния y(t) в момент t. Следовательно, v является функцией от y и t: v = v(y, t), а от управления u и его вариаций функция v = v(y, t) не зависит. Она вполне определяется значениями y, t .

Интервал (t, T) разделим на два интервала (t, t + t) и (t + t, T) и выражение (4.8) запишем в виде:

.

Согласно принципу оптимальности последний участок также является оптимальным:

(4.9)

Обозначим:

, (4.10)

где - приращение вектора фазовых координат за время . Оно определяется согласно уравнениям движения (4.1). Подставляя из (4.10) в равенство (4.9), получим:

.

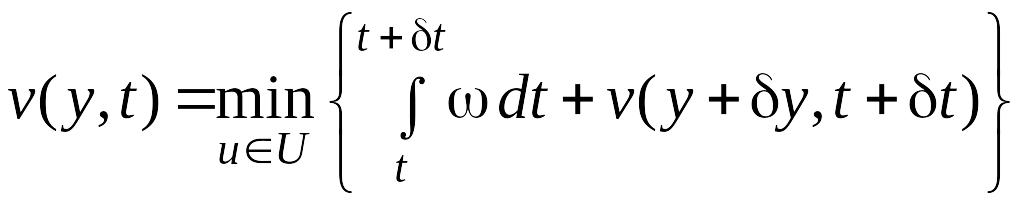Хотя функция зависит только от фазовых координат и времени, ее нельзя выносить за знак . Значение приращения за время зависит от управления в интервале . Но не зависит от управления в интервале , и ее можно внести под знак . Введем под знак минимума и разделим на :

.

Учитывая, что

;

,

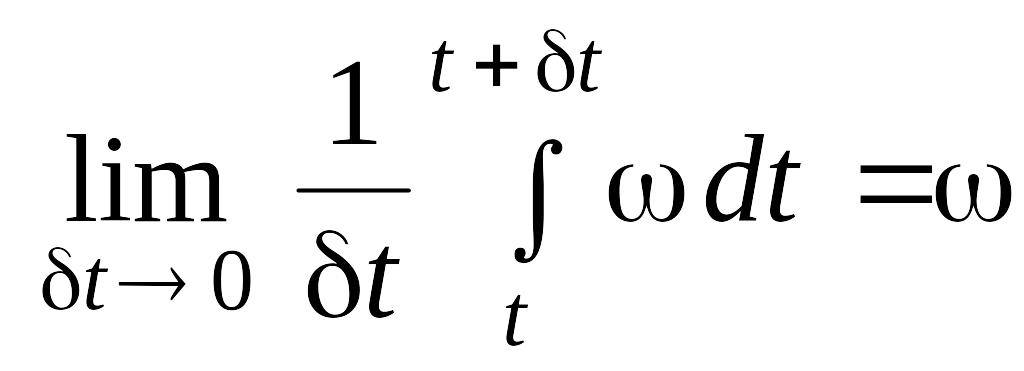получим основное уравнение метода динамического программирования:

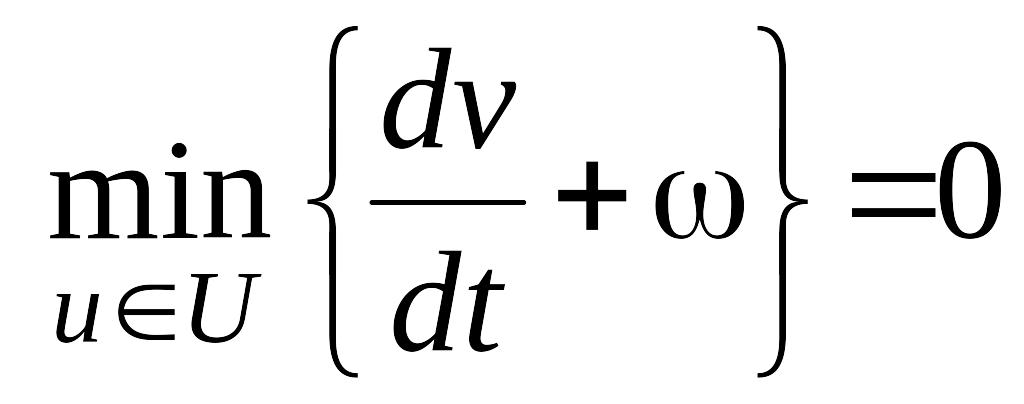. (4.11)

Это соотношение состоит из двух утверждений:

1. выражение 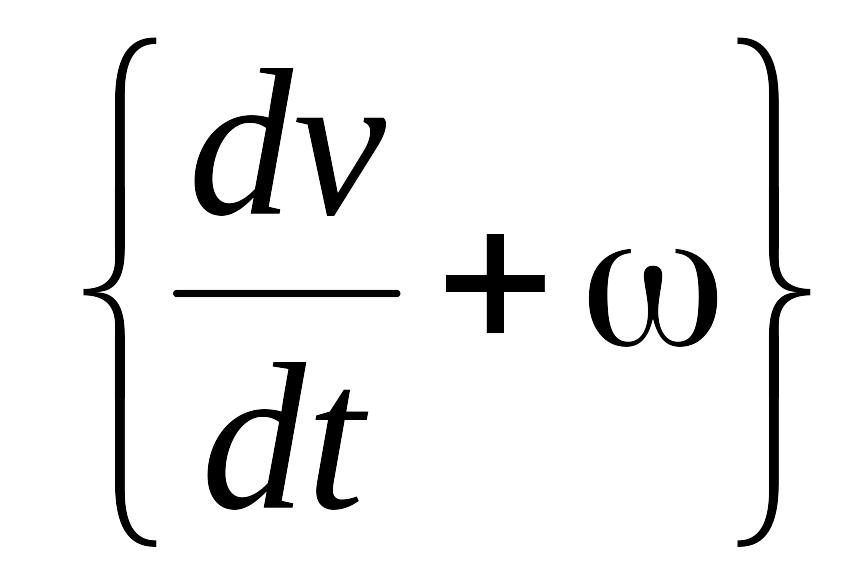достигает минимума. Это утверждение служит для определения оптимального управления ;

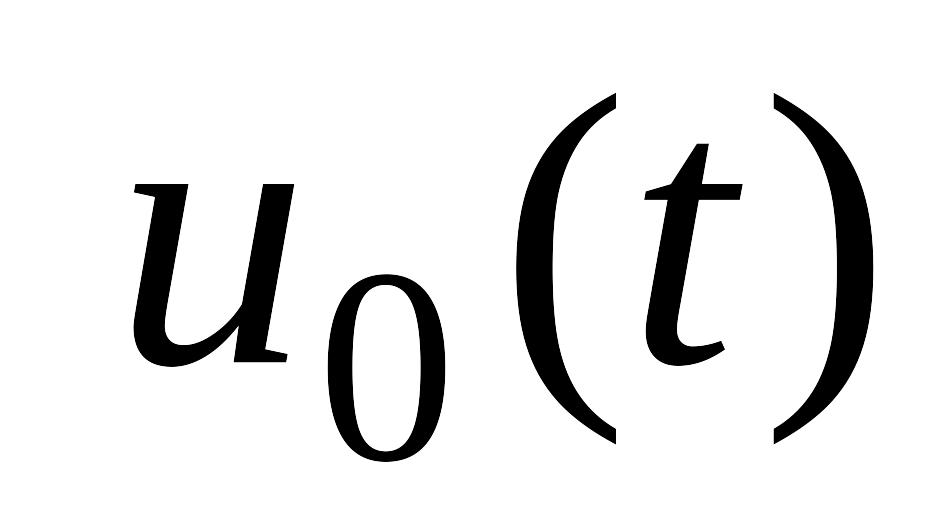2. выражение при оптимальном управлении равняется нулю. Утверждение служит для определения функции .

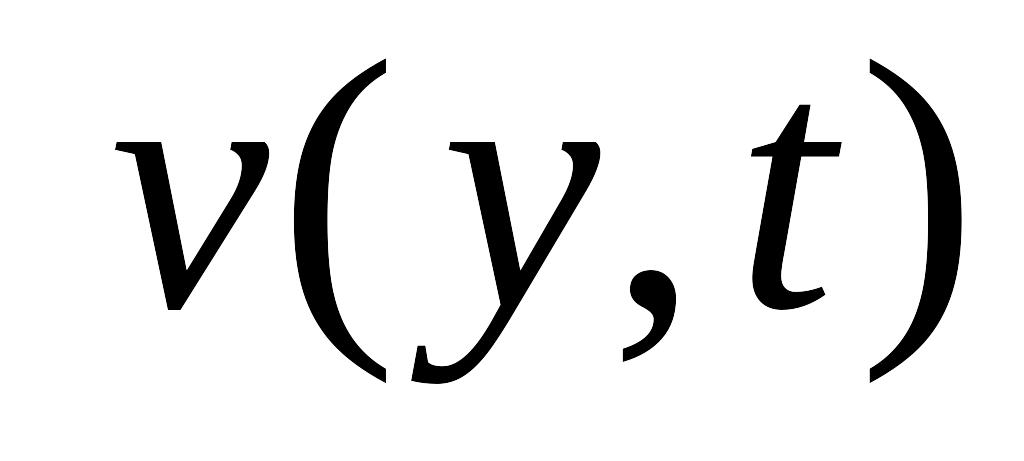Если - управление, минимизирующее выражение , то основное уравнение метода динамического программирования

(4.12)

Здесь зависит от управления по определению, функция же не зависит от него. Тем не менее, производная от управления зависит. В этом можно убедиться, если ее представить в виде

и y_i’ заменить согласно системе (4.1):

. (4.13)

Подставляя (4.13) в (4.12) получим уравнение Р.Беллмана:

. (4.14)

Это уравнение в частных производных относительно , которое после подстановки становится нелинейным. Согласно определению v (4.8) при должно выполняться конечное условие

.

В случае бесконечного интервала при процесс должен быть асимптотически устойчивым, т.е. .

В том случае, когда рассматривается функционал Больца

(4.15)

Уравнение (4.12) сохраняет силу, функция v в момент должна удовлетворять условию

. (4.16)