В процессе доказательства теоремы 6 мы выяснили, что

(;· =c; ··   , |c; ··| = k  (;· = k  .

Также b;· ||  , ||= |b;· (s)| , и мы убрали модуль в формуле (1) так, что

=–b;· ·   b;· =– .

Итак, мы уже знаем производные (;· и b;·. Найдем (;· :

 = ´  (;· = b;·´´(;· = –´´ k  = –(–)k (–).

Запишем все формулы вместе:

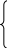(;· = k ,

(;· = – k   , (4)

b;· = – .

Они называются формулами Френе.

Из этих формул и теорем о существовании и единственности решений систем дифференциальный уравнений вытекает основная теорема теории кривых.

Теорема 8. Если некотором интервале IR заданы непрерывная функция s и гладкая функция k(s)>0, то существует кривая  класса С², для которой s будет естественным параметром, k – кривизной, а  – кручением. Такая кривая определяется однозначно с точностью до положения в пространстве, т.е. любые две такие кривые совмещаются движением.

§7. Вид кривой в подвижном репере

Пусть  – кривая класса с³, PÎ – точка в которой k0, 0, {P, , , } – подвижной репер. Он определяет декартову систему координат с началом Р. Обозначим координаты х, у, z.

Пусть r; (= c(s) – уравнение кривой с естественным параметром и P=c(0). Разложим c(s) в ряд Тейлора в окрестности s=0:

c(s) = c(0) + s c; ·(0) + c; ··(s) + c;···(s) + s³ (;\s\up8(–((s),

где (;\s\up8(–((s) – бесконечно малый вектор при s0. Поскольку c(0) – начало координат, то c(0) = o;\s\up8(–( . Мы также знаем, что c; · = , c; ·· = k. Тогда с помощью формул Френе находим

c;··· = k; ·k(;· = k; ·k(– k  ) = k; ·– k²k.

c(s) = s× +  + (k; ·– k²k) + s³ (;\s\up8(–((s).

Значит, если отбросить бесконечно малые величины порядка более 3, то

c(s) =  +  ,

Поэтому параметрические уравнения кривой в окрестности точки P в координатах будут иметь вид:

е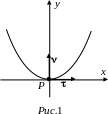 сли для каждой координаты оставить только величину, имеющую наибольшее значение при малых s.

Соприкасающаяся плоскость парал-лельна  и , т.е. в нашей системе координат это будет плоскость Оxy. Поэтому проекция кривой на эту плоскость будет иметь уравнение

Вид этой проекции в ближайшей окрестности точки P изображен на рисунке 1 (парабола).

С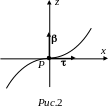 прямляющая плоскость параллельна  и , т.е. в нашей системе координат это будет плоскость Оxz. Поэтому проекция кривой на эту плоскость будет иметь уравнение

Вид этой проекции в ближайшей окрестности точки P изображен на рисунке 2 (кубическая парабола).

Н ормальная плоскость параллельна  и , т.е. в нашей системе координат это будет плоскость Оyz. Поэтому проекция кривой на эту плоскость будет иметь уравнение

Вид этой проекции в ближайшей окрестности точки P изображен на рисунке 3 (полукубическая парабола).