Шпаргалки по ТОЭ 3 семестр
.doc
Электрическим током называется упорядоченное движение частиц - носителей тока. Постоянный ток – ток неизменимый во времени. Электрический ток характеризуется силой тока.
При перемещении элементарного заряда выделяется следующая энергия:
|
Резистивный
элемент характеризуется своим
сопротивлением.
G
– проводимость
=
|
Реальные
источники электрической энергии
имеет ЭДС
1.
2.
Пусть
|
9. Эквивалентное преобразование источников. |
|
11. МКТ. Порядок расчета: 1. Выбрать направления и задать номера контурных токов. Если есть ИТ, то номер контурного тока, проходящего через ИТ, рекомендуется задавать последним. Через ИТ должен проходить только один контурный ток! 2. Составить систему независимых уравнений:
3.
Решить систему и определить напряжения
(токи) цепи.
|
12. МУН. Порядок расчета: 1. Преобразовать ИН в ИТ (если возможно)
2.
Расставить узлы преобразованной цепи
(каждому узлу соответствует его
3. Составить систему независимых уравнений:
4.
Решить систему и определить напряжения
(токи) цепи.
5. Вернуться к исходной цепи. |
13. Метод эквивалентного источника напряжения. |
14. Метод эквивалентного источника тока. |
|
15. L-элемент цепи. Основная х-ка, ВАХ, закон коммутации.
L-элемент
– двухполюсник, характеризующий одну
из сторон ЭМ-процесса, а именно
накопление энергии магнитного поля.
Основная х-ка – индуктивность.
Следовательно:
1.
стен
ток на L
к
моменту времени
|
16. С-элемент. Основная х-ка, ВАХ, закон коммутации.
С-элемент
– такой
двухполюсник, который характеризует
одну из сторон ЭМ-процесса, а именно
запасание энергии ЭП. Основная х-ка
– емкость:
тикой.
Построим ВАХ элемента
1.
2.
Если в цепи известно напряжение на С
к
моменту
3.
При постоянном воздействии
|
19. Любой выходной сигнал динамической цепи 1ого порядка при коммутации имеет вид:
Алгоритм:
1.
2.
3.
4.
Определяем постоянную времени
5.
Находим постоянную А:
6. Ответ: имеет вид выражение (1), содержащее полученные в результате расчетов значения. Расчет переходных процессов в разветвленной цепи RL/C. |
20. Процессы в последовательной RLC при подключении к источнику const U. Апериодический, граничный и режим затухающих колебаний. |
|
21. Определение порядка цепи. Особенности коммутации в цепях при наличии емкостных контуров и индуктивных сечений. Порядок
цепи
– это максимальная степень
дифференциального уравнения. Во
многих случаях порядок равен
накопительных элементов ( |
23. Единичная ступенчатая, единичная импульсная и функция единичного наклона. Связь м/у ними. Применение в ТОЭ. Некоторые стандартные сигналы, на которые необходимо находить отклики (из них можно выразить все остальные).
Используется для выделения функции в некотором времени.
т.о.
|
24.
Переходная
характеристика цепи. Импульсная
характеристика. Характеристика
Переходная
характеристика
Импульсная
характеристика:
Характеристика
|
26. Интеграл наложения через импульсную характеристику.
Пусть
реакции,
получим
Интеграл
Дюамеля:
|
|
26. Интеграл наложения через импульсную характеристику.
Пусть
реакции,
получим
Интеграл
свертки:
|
26. Интеграл наложения через импульсную характеристику.
Пусть
реакции,
получим
Интеграл
свертки:
Интеграл
Дюамеля:
|
27. Среднее и действующие значение гармонической функции. Среднее
за период T
значение
определяется как
|
30. Закон Ома и Кирхгофа в комплексной форме. Формы записи комплексного числа:
Закон токов Кирхгофа:
Закон напряжения Кирхгофа:
Проводя
аналогичные рассуждения
Закон Ома в комплексной форме:
|
|
31. R-эл-т в синусоидальном режиме. По закону Ома:
Теперь
подставим
Теперь напишем для комплексного сопротивления:
Комплексная
проводимость:
|
32. L-эл-т в синусоидальном режиме. (33. С-эл-т в sin-режиме – а.)
Теперь
пусть
|
34. Мощность в синусоидальном режиме. Пусть
через элемент течет ток
Активная
мощность:
Реактивная
мощность:
Активная
мощность зависит от
|
35. Мощность в комплексной форме.
|

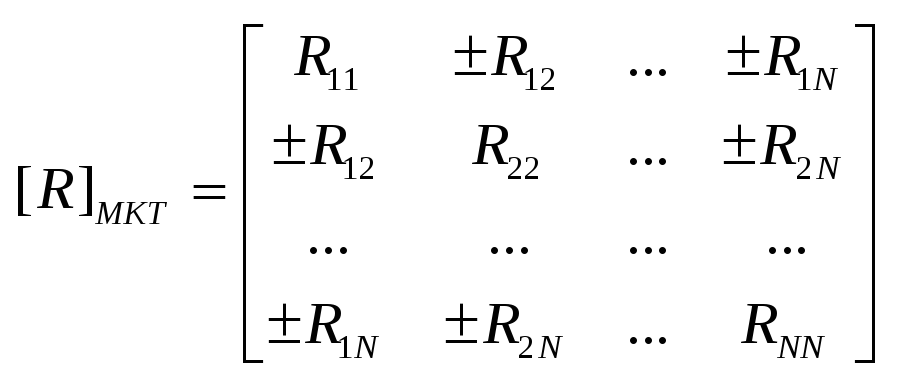 ,
где
,
где
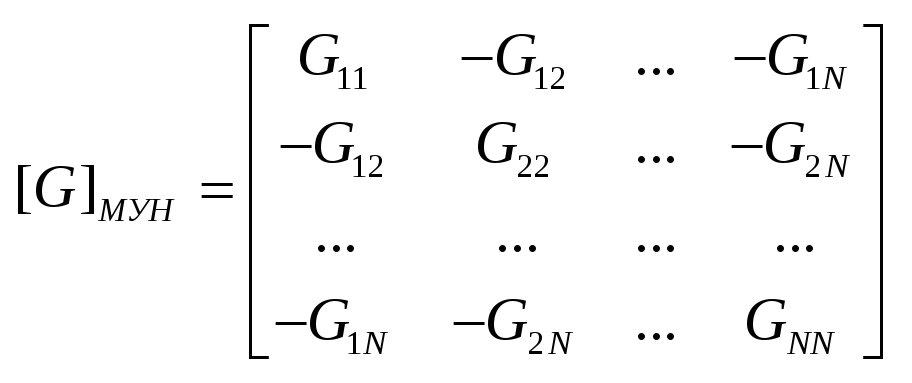 ,
где
,
где