Классификация внешних нагрузок. Все внешние нагрузки можно классифицировать так: F[кН], M[кН*м], q[кН/м]. Сосредоточенные: статические(нагрузки, изменяющие величину или точку приложения с очень малой скоростью, так что при возникающими при этом ускорениями можно пренебречь); динамические (нагрузки, изменяющиеся во времени с большой скоростью. Действие их сопровождается возникновением колебаний) . Распределённые: поверхностные(давление ветра, воды, снега); объёмные(сила тяжести, сила инерции);статические. По продолжительности действия: постоянные(нагрузки, действующие непрерывно в течение всего срока службы конструкции – собственный вес конструкции); временные(имеют ограниченную продолжительность действия – снег на крыше здания).
Классификация элементов. Все элементы в строительной конструкции разделяют по геометрическим характеристикам на ряд типов: фундаменты – массивные тела, все основные размеры которых одного порядка; плиты – плоские тела, толщина которых мала по сравнению с остальными размерами; оболочки – тела, внешние контуры которых образованы криволинейными поверхностями; стержни(брусья; прямолинейные, криволинейные); балка – стержень, работающий преимущественно на изгиб; колонна, стойка – вертикальный стержень, работающий на сжатие; оси, валы – вращающиеся машиностроительные элементы.
Расчетная схема. В СМ расчет реальных конструкций производят с помощью расчетных схем. При составлении расчетных схем надо иметь в виду, что некоторые правила ТМ применять нельзя. Нельзя переносить силы по линии их действия и нельзя заменять силы их равнодействующей.
Основные гипотезы СМ. 1) Материал конструкции имеет сплошное однородное строение. 2)Материал идеально упругий, т.е при снятии нагрузки тело возвращается в первоначальное состояние. 3)Материал изотропны: обладает одинаковыми свойствами во всех направлениях. 4)Деформации материала в каждой его точке прямо пропорциональны напряжениям в этой точке(Закон Гука). 5) Принцип независимости действия сил. 6) Гипотеза плоских сечений: поперечное сечение бруса, плоское и нормальное к оси бруса до приложения нагрузки, остаётся плоским и нормальным к оси и при действии нагрузки.
Внутренние силы. Метод сечений. Внутренние силы – силы взаимодействия между частями конструкции или между отдельными частицами элемента конструкции. Возникают под действием внешних сил и определяются методом сечений. Внутренние силы должны быть распределены по сечению так, чтобы деформационной поверхности сечения при совмещении левой и правой частей в точности совпадали. Это условие совместности деформаций.
Напряжения. Нормальные и касательные напряжения. Напряжение – величина внутреннего усилия, приходящегося на единицу площади поперечного сечения. Совокупность напряжений для множества площадок, проходящих через точку, называется напряженным состоянием в точке.
Растяжение – сжатие. Продольные силы, эпюры. Центральное растяжение – такой вид напряженно-деформационного состояния, при котором в поперечном сечении бруса возникают только продольные силы. Эпюра продольных сил – график, каждая ордината которого равна значению продольной силы в данном сечении.
Нормальные напряжения при растяжении – сжатии.
Абсолютные и относительные деформации. Закон Гука.
Напряжение с учетом собственного веса конструкции.
Деформации с учетом собственного веса конструкции.
Условие прочности при растяжении – сжатии.
Условие прочности при растяжении (сжатии) призматического стержня для стержня из пластического материала (т. е. материала, одинаково работающего на растяжение и сжатие) будет иметь вид:
где —допускаемое напряжение. Напряжение в условии подставляется по модулю, так как знак в этом случае роли не играет. Для стержней из хрупких материалов, неодинаково сопротивляющихся растяжению и сжатию, знак напряжения имеет принципиальное значение, и условие прочности приходится формулировать отдельно для растяжения и сжатия.
Расчет по допускаемым напряжениям.
Исходя из условия прочности, решаются 3 основные задачи механики материалов конструкций: проверка прочности – этот расчет проводится, если нагрузка, сечение стержня и его материал заданы. Расчет заключается в том, что определяется фактический коэффициент запаса прочности и сравнивается с нормативным коэф-том запаса. Подбор сечения – в этом расчете по заданной нагрузке определяются размеры поперечного сечения стержня из заданного материала. Минимальное значение получим, если в условии прочности принять знак равенства. Определение допускаемой нагрузки, т.е максимального значения нагрузки, которое допускает данный элемент конструкции при выполнении условия прочности.
Напряжение в наклонных сечениях при растяжении-сжатии.
Расчет статически неопределимых систем при растяжении – сжатии. Кроме уравнений статики для расчета таких систем приходится привлекать дополнительные условия, описывающие деформацию элементов данной системы. Их называют уравнениями перемещений или уравнениями совместности деформаций (сам метод решения называется методом сравнения деформаций). 1-определить общее число неизвестных и число «лишних» неизвестных; 2-составить уравнения статики; 3- составить дополнительные уравнения в количестве, равном числу лишних неизвестных.
Температурные и монтажные напряжения. В результате изменения температуры в элементах конструкции, возникают температурные напряжения. Если бы один конец стержня был свободным, то в результате нагрева стержень удлинился бы и напряжения не возникли. Т.к заделка не даёт стержню удлиниться, то он испытывает сжатие, в нём возникают продольные силы и напряжения. Монтажные напряжения – которые возникают при сборке конструкции в результате неточного изготовления отдельных её элементов.
Опытное изучение свойств материалов. Диаграмма растяжения малоуглеродистых сталей. Материал проверяют на растяжение, сжатие, изгиб, кручение, сдвиг, твёрдость. Основной вид испытания – на растяжение. Из материала изготавливают образцы: цилиндрические, плоские. Для испытаний на растяжение используют специальные разрывные машины, позволяющие в процессе испытания определить усилия и деформации. Строится диаграмма растяжения. Характер диаграммы зависит от свойств материалов.
Диаграмма напряжений. Основные характеристики материала. Чтобы построить диаграмму напряжений, нужно знать не только характеристики материала, но и размеры образца.
Понятие о пластических и хрупких материалах. Пластические – это материалы, которые приобретают значительные деформации, прежде чем разрушиться. Опыты показывают, что пластические материалы одинаково работают на растяжение и сжатие. Хрупкие – материалы, которые вплоть до разрушения имеют незначительные деформации (бетон, чугун, камень, кирпич). Хрупкие материалы на сжатие работают лучше, чем на растяжение. Главная задача расчета конструкции - обеспечить её нормальную эксплуатацию , в процессе которой элементы конструкции не будут разрушаться и в них не будет возникать текучесть.
Диаграммы сжатия чугуна, древесины, стали.
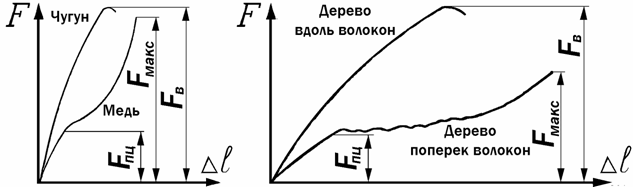
Сложное напряженное состояние. Главные площадки и главные напряжения. В каждой точке любого напряженного тела можно указать три взаимно перпендикулярные площадки, через которые передаются 3 главные напряжения, 2 из которых имеют экстремальные значения: одно является наибольшим нормальным напряжением, другое – наименьшим, третье – промежуточное. В каждой точке напряженного тела можно выделить элементарный кубик, гранями которого служат главные площадки. Различают 3 вида напряженного состояния: объёмное – когда все три главных напряжения не равны нулю. Плоское- когда одно главное напряжение равно нулю. Линейное – когда два главных напряжения равны нулю.
Напряжения при линейном напряженном состоянии. Напряженное состояние называется линейным или одноосным, если два главных напряжения равны нулю. Проверка прочности при линейном напряженном состоянии проводится по условию прочности:
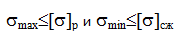В
сложном напряженном состоянии проверку
прочности проводят по гипотезам
прочности по эквивалентному напряжению:
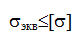Величина
σэкв определяется, исходя из принятого
критерия эквивалентности, лежащего в
основе одной из гипотез разрушения
или гипотез прочности, при котором
сложное напряженное состояние заменяется
эквивалентным ему растяжением или
сжатием.Напряжения при плоском напряженном состоянии. Нормальное напряжение положительно, если оно растягивающее, касательное напряжение положительно, если оно стремится повернуть рассматриваемую часть элемента относительно внутренней точки по часовой стрелке.
Плоское напряженное состояние. Прямая и обратная задача. По известным главным напряжениям: s1= smax, s2= smin требуется определить для площадки, наклоненной под заданным углом (a) к главным площадкам, нормальные и касательные
напряжения:
Обратная задача. По известным нормальным и касательным напряжениям, действующим в двух взаимно перпендикулярных площадках, найти главные (max и min) напряжения и положение главных площадок.
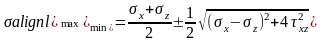
Деформации при объёмном напряжённом состоянии. Закон Гука. В случае объемного напряженного состояния деформации наблюдаются в трех взаимно перпендикулярных направлениях одновременно.
Геометрические характеристики плоских сечений. Статический момент сечения. Центр тяжести. Площадь сечения – одна из главных геометрических характеристик сечения. Площадь всего сечения, состоящего из множества элементарных площадок:
Статический момент т сечения – сумма произведений элементарных площадок на расстоянии до данной оси, распространенная на всю площадь сечения:
Координаты центра тяжести сечения сложного сечения определяем так: сложное сечение разбиваем на простые фигуры; определяем площадь и координаты центра тяжести каждой фигуры; вычисляем статические моменты простых фигур по ф-ле и вычисляем координаты центра тяжести:
Осевой момент инерции сечения. Полярный момент инерции сечения. Центробежный момент сечения инерции. Осевой момент сечения инерции – сумма произведений элементарных площадок на квадрат расстояния до оси распределенной на всю площадь. Полярный момент - сумма произведений элементарных площадок на квадрат расстояния до полюса, распределенного на всю площадь сечения. Центробежный момент – сумма произведений элементарных площадок до координатных осей распространенных на всю площадь сечения.
Зависимость между осевым и полярным моментами сечения.: