
- •25. Процесс принятия решений: этапы, участники, основные задачи принятия решений.
- •26. Бинарные отношения. Операции над отношениями. Свойства бинарных отношений.
- •27. Бинарные отношения. Виды бинарных отношений. R-оптимальность.
- •28. Функции выбора. Логические формы функций выбора.
- •29. Функции выбора. Нормальные функции выбора.
- •30. Критериальное пространство. Бинарные отношения в критериальном пространстве.
- •31. Методы многокритериальной оптимизации. Метод линейной свертки
- •32. Методы многокритериальной оптимизации. Метод идеальной точки.
- •33. Методы многокритериальной оптимизации. Выбор с учетом числа доминирующих критериев.
- •34. Метод многокритериальной оптимизации. Метод анализа иерархий
- •35. Основная задача линейного программирования. Методы решений.
- •36. Двойственные задачи линейного программирования.
- •37. Транспортная задача.
- •38. Задача о назначении.
- •39. Динамическое программирование. Задача о замене оборудования.
- •40. Динамическое программирование. Мультипликативная задача.
- •41. Принятие решений в условиях полной неопределенности, в условиях риска
- •42. Принятие решений в условиях конфликта (Элементы теории игр). Основные понятия.
- •43. Задачи теории игр. Классификация игр.
- •44. Матричные игры. Решение матричной игры в чистых стратегиях. Смешанные стратегии.
- •45. Матричные игры. Сведение матричной игры к задаче линейного программирования.
- •46. Графоаналитические методы решения матричных игр.
- •47. Метод Брауна-Робинсон.
- •48. Методы экспертных оценок. Множества оценок экспертов.
- •49. Методы экспертных оценок. Типы шкал для измерения критериев.
- •Шкалы качественных признаков
- •Шкалы количественных признаков.
- •50. Методы обработки экспертной информации.
32. Методы многокритериальной оптимизации. Метод идеальной точки.
Критериальное пространство.
Пусть альтернативы из множества Ω рассматриваются относительно некоторых свойств f1,…,fn.
Если свойство f – альтернативы может быть выражено числом, т.е. существует то такое свойство называют критерием, а значение φ(x) называют оценкой альтернативы x по критерию f.
Аспектом называют сложное свойство, которое агрегирует в себе другие свойства.
Если все свойства альтернатив f1,…,fn из множества Ω являются критериями, т.е. , то тем самым определено отображение так, что .
Считая, что множество Ω содержится в , пространство будем называть критериальным пространством. векторы в .
Пусть
.
Определим функцию выбора
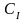 на Ω следующим образом. Положим
на Ω следующим образом. Положим
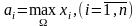 .
Таким образом,
.
Таким образом,
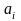 является максимально возможным значением
по i-му
критерию. Точка
является максимально возможным значением
по i-му
критерию. Точка
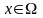 такая, что
такая, что
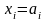 является решением обычной однокритериальной
задачи оптимизации. Предполагается,
что Ω – замкнутое ограниченное множество
в
,
поэтому решения указанных задач
существуют.
является решением обычной однокритериальной
задачи оптимизации. Предполагается,
что Ω – замкнутое ограниченное множество
в
,
поэтому решения указанных задач
существуют.
Положим
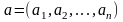 .
Точка а
называется идеальной.
Смысл названия связан с тем, что такие
точки оптимальны сразу по всем критериям:
получить большее значение ни по одному
критерию невозможно. Очевидно, что для
всех
справедливо аРх.
Как правило, идеальная точка а
не принадлежит Ω.
.
Точка а
называется идеальной.
Смысл названия связан с тем, что такие
точки оптимальны сразу по всем критериям:
получить большее значение ни по одному
критерию невозможно. Очевидно, что для
всех
справедливо аРх.
Как правило, идеальная точка а
не принадлежит Ω.
Зададим для всех точек функцию, являющуюся евклидовымрасстоянием между точками х и a:
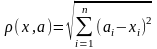 .
.
Методом идеальной точки называется принцип оптимальности, который может быть выражен с помощью функции выбора СI:
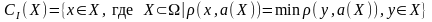 ,
,
где а(Х) – точка, идеальная для множества X.
Решение
общей задачи оптимизации <Ω, ОП>, в
которой принцип оптимальности выражается
функцией выбора COП
= СI,
сводится к решению обычной однокритериальной
задачи оптимизации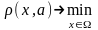 .
.
x3
–
решение
задачи оптимизации с использованием
метода идеальной точки.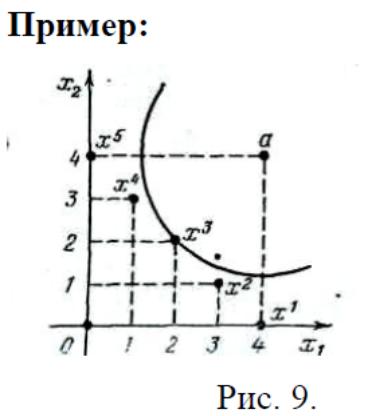
Теорема:
Пусть Ω выпукло. Тогда CI(Ω) состоит из одной точки.
Доказательство.
Пусть
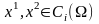 .
Это значит, что точки
.
Это значит, что точки
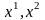 находятся на равном расстоянии от точки
а.
Проведем двумерную плоскость через
находятся на равном расстоянии от точки
а.
Проведем двумерную плоскость через
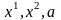 и
обозначим через
и
обозначим через
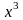 середину отрезка с концами в
.
В прямоугольном треугольнике
середину отрезка с концами в
.
В прямоугольном треугольнике
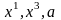 катет
катет
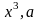 меньше, чем гипотенуза
меньше, чем гипотенуза
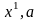 .
В силу выпуклости Ω точка
принадлежит Ω. Так как
.
В силу выпуклости Ω точка
принадлежит Ω. Так как
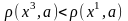 ,
то
,
то
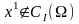 .
Полученное противоречие доказывает
утверждение.
.
Полученное противоречие доказывает
утверждение.
Для
произвольных множеств
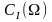 может
состоять из нескольких точек.
может
состоять из нескольких точек.
Функция выбора обладает следующим свойством.
Теорема:
Для
любого
имеет место включение
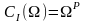 .
.
Доказательство.
Пусть
а – идеальная точка,
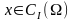 .
Предположим, что теорема неверна. Это
значит, что для некоторой точки
.
Предположим, что теорема неверна. Это
значит, что для некоторой точки
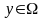 выполнено уРх. С учетом, что aPx
имеем аРх, аРу и уРх. Положим а – х = (а –
у) + (у – х). В силу аРу и уРх все компоненты
векторов а – у и у – х неотрицательны.
Поэтому каждая компонента вектора а –
х не меньше, чем соответствующая
компонента а – у, и найдется компонента,
которая строго больше. Следовательно,
длина вектора а – х больше, чем длина
вектора а – у. Но это противоречит тому,
что
.
Полученное противоречие доказывает
теорему.
выполнено уРх. С учетом, что aPx
имеем аРх, аРу и уРх. Положим а – х = (а –
у) + (у – х). В силу аРу и уРх все компоненты
векторов а – у и у – х неотрицательны.
Поэтому каждая компонента вектора а –
х не меньше, чем соответствующая
компонента а – у, и найдется компонента,
которая строго больше. Следовательно,
длина вектора а – х больше, чем длина
вектора а – у. Но это противоречит тому,
что
.
Полученное противоречие доказывает
теорему.
