27. Бинарные отношения. Виды бинарных отношений. R-оптимальность.

Бинарные отношения.

Свойства предметов окружающего мира, относимые к наборам, состоящим из n предметов, называются n-арными отношениями. (n – любое натуральное число). Т. о., бинарные отношения – свойства предметов, относимые к парам предметов.

Понятие бинарного отношения позволяет формализовать операции попарного сравнения. Поэтому они широко используются в теории выбора. Отношением R на множестве X называется подмножество R множества X × X , т.е. .

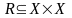Содержательный смысл такого определения состоит в том, что задание подмножества R в множестве X×X определяет, какие пары находятся в отношении R. Если пара <х, у> входит в R, то пишут xRy.

Для того чтобы задать отношение R на множестве X, нужно указать все пары <х, у>ͼX×X, которые содержатся Свойства предметов окружающего мира, относимые к наборам, состоящим из n предметов, называются n-арными отношениями. (n – любое натуральное число). Т. о., бинарные отношения – свойства предметов, относимые к парам предметов.

Важный момент в задаче принятия решений состоит в изучении (задании) системы предпочтений ЛПР (лицо, принимающее решения). Язык бинарных отношений – язык описания системы предпочтений ЛПР.

Простейшая ситуация, которая позволяет сделать обоснованный выбор из нескольких объектов, возникает, когда задан один "критерий качества", позволяющий сравнить любые два объекта, четко указать, какой из них лучше, и выбрать тот (или те), на котором этот критерий достигает максимального значения. Однако в большинстве реальных ситуаций выделить один такой критерий не удается; более того, часто вообще трудно выделить критерии. Тем не менее, для некоторых пар объектов можно указать, какой из объектов пары лучше (предпочтительнее) другого. В таких случаях говорят, что эти два объекта находятся в в R, т.е. пары <х, у>ͼ X², для которых выполняется отношение R. Кроме непосредственного указания всех пар, для которых выполняется отношение R, существуют три основных способа задания отношения: задание отношения матрицей; задание отношения графом; задание отношения сечениями.

Задание матрицей.

Пусть X состоит из n элементов, R есть отношение на X. Занумеруем элементы множества X целыми числами от 1 до n. Построим квадратную таблицу размера nхn. Ее i-я строка соответствует i-му элементу множества X, обозначенному через xi, а j-й столбец - элементу xj. На пересечении i-й строки и j-гo столбца ставится единица, если выполнено xi R xj, и нуль - в противном случае. Обозначим элемент, стоящий на пересечении i-й строки и j-гo столбца, через aij. Общее правило задания матрицы отношения R формулируется так: aij (R)=l, если выполнено xi R xj, aij (R)=0, если не выполнено xi R xj (i,j = 1,…,n).

Задание графом.

Поставим в соответствие элементам конечного множества X вершины графа x1 , …, xn (при некоторой нумерации). Проведем дугу от xi к xj тогда и только тогда, когда выполнено xi R xj (при i=j дуга (xi,xj) превращается в петлю при вершине xi).

Задание сечениями.

Рассмотрим отношение R на множестве X. Верхним сечением R+(x) называется множество элементов у таких, что <у, x >ͼR: R+(x) = {уͼX |<у,х >ͼR}; аналогично определяется нижнее сечение: R-(х) = {уͼX |<х,у >ͼR}. Таким образом, множество R-(x) -это множество всех элементов уͼX, с которыми фиксированный элемент хͼX, находится в отношении R. Множество R+(х) - это множество всех элементов уͼX, которые находятся в отношении R с фиксированным элементом xͼX.

Виды бинарных отношений.

1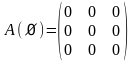 . Пустое отношение.

Отношение, заданное на множестве X, называется пустым (обозначение Ø), если оно не выполняется ни для одной пары (x, y)ͼX².

2. Полное отношение.

О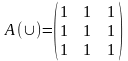 тношение, заданное на множестве X, называется полным (обозначение U), если оно выполняется для всех пар (x, y)ͼX².

3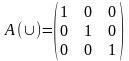 . Отношение тождества.

Отношение, заданное на множестве X, называется отношением тождества (обозначение E), если оно выполняется для всех пар (x, y)  X² таких, что x и y – один и тот же элемент.

4. Отношение эквивалентности (~).

Бинарное отношение R называют отношением эквивалентности, если оно рефлексивно, симметрично и транзитивно.

Теорема:

Отношение R на X является отношением эквивалентности тогда и только тогда, когда существует разбиение: 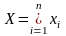и 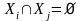при i≠j такое, что xRy и существует подмножество 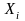, содержащее x и y.

Например, отношениями эквивалентности являются: отношение «быть на одном курсе» на множестве студентов одного факультета, «иметь одинаковый остаток при делении на 3» на множестве натуральных чисел.

5. Отношение нестрогого порядка.

Рефлексивное, антисимметричное и транзитивное отношение называется отношением нестрогого порядка на множестве X.

6. Отношение строгого порядка (<).

Антифлексивное, асимметричное и транзитивное отношение называется отношением строгого порядка на множестве X.

7.Отношение частичного порядка.

Отношение порядка R (строгого или нестрогого) называется отношением частичного порядка, если существуют несравнимые по R элементы.

8. Отношение линейного порядка.

Отношение порядка на множестве X , для которого любые два элемента сравнимы, т. е. для любых x, y Xx<y , x=y или y<x , называется отношением линейного порядка.

9. Отношение толерантности.

Рефлексивное, симметричное и нетранзитивное отношение на множестве X называется отношением толерантности на множестве X (отношение “быть знакомым”).

10. Отношение доминирования.

Антирефлексивное и асимметричное отношение на множестве X будем называть отношением доминирования. Будем говорить, что x доминирует y (x>>y), если x в каком-либо смысле превосходит y. Таким образом, отношение строго порядка является частным случаем отношения доминирования, при котором дополнительно требуется транзитивность. В общем случае для доминирования как транзитивность, так и ацикличность могут не иметь места.

R-оптимальность.

Элемент х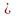 X называется максимумом по отношению R, заданному на X, если для всех у X выполнено xRy. Аналогично, х X называется минимумом по отношению R, заданному на X, если для всех у X выполнено yRx. Максимумы и минимумы по отношению к R могут существовать или не существовать. От максимума и минимума следует отличать понятия мажоранты и миноранты по отношению R. Элемент х X называется мажорантой по отношению R, заданному на X, если для всех у X выполнено y x. Аналогично, х X называется минорантой по отношению R, заданному на X, если для всех у X выполнено x y.

Пусть R - произвольное отношение на множестве X; X⁺(R) - множество максимумов по отношению R; X₊(R) - множество мажорант;

X^-(R)- множество минимумов; X_-(R) -множество минорант.

Множество X₊(R), играющее важную роль в теории выбора, называется также множеством недоминируемых по R элементов; входящие в него элементы называются R-оптимальными.