40. Получение спектральной плотности прямоугольного импульса. Приведите графическое представление модуля и аргумента спектральной функции прямоугольного импульса.

Прямоугольный импульс. Для нахождения спектральной плотности импульсных сигналов, представляемых отрезками прямых будем использовать прием, заключающийся в дифференцировании исходного сигнала необходимое число раз, чтобы он предстал в виде нескольких δ – функций. Модуль и аргумент спектральной плотности прямоугольного импульса, показанного на рис. 160 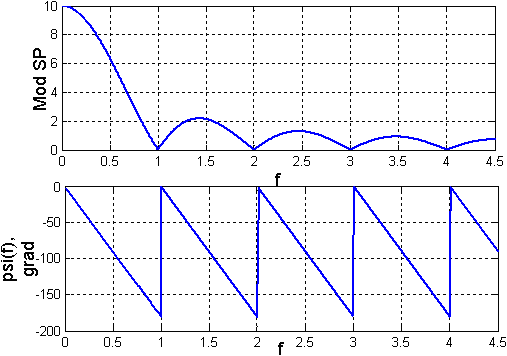. модуль спектральной функции (амплитудно – частотный спектр) и ее аргумент (фазочастотный спектр) . Под шириной спектра здесь и в дальнейшем будем понимать частотный интервал, в пределах которого модуль спектральной плотности не меньше некоторого наперед заданного уровня, например 0.1S_MAX. Нули спектральной функции прямоугольного импульса определяются соотношением

41. Определите понятия непрерывного и дискретного сигналов. Запишите и проанализируйте выражение для спектральной плотности дискретизированного сигнала. Спектры сигналов, используемых в электротехнике и электронике, при всем их многообразии могут быть разделены на два вида – дискретные и сплошные. Дискретные спектры состоят из дискретного ряда гармонических колебаний. Обычно с помощью таких спектров характеризуют периодические негармонические сигналы, которые широко используются в электронике в цепях питания, синхронизации, развертки. Спектр сигнала конечной длительности содержит спектральные составляющие, интервал между которыми стремиться к нулю. Такой спектр с бесконечно малыми интервалами между смежными составляющими называют сплошным. Интеграл, как комплексная функция частоты, получил название спектральной плотности одиночного импульса. Отсюда следует, что коэффициенты комплексного ряда Фурье связаны со спектральной плотностью одиночного импульса соотношением Для повышения оперативности ДПФ применяют специальные алгоритмы быстрого преобразования Фурье (БПФ), которые сокращают количество вычислительных операций и тем самым ускоряют счет на ЭВМ. Выигрыш в скорости вычислений по сравнению с традиционным ДПФ достигает сотен и тысячи раз. Пример расчета спектральной плотности прямоугольного импульса, аналогичного ранее рассмотренному, с помощью БПФ показан на рис. Широко применяемой на практике является форма сигнала в виде группы равноотстоящих друг от друга импульсов одинаковой формы. Предположим, что рассматриваем пачку, состоящую из n импульсов прямоугольной формы. пример графической зависимости (АЧХ и ФЧХ) модуля и аргумента спектральной плотности пачки из 4-х импульсов.

42. Определите понятие энергетического спектра сигнала. Поясните, для чего оно используется. Энергетический спектр есть квадрат модуля спектральной плотности и не зависит от ее фазы. Если известен ток i(t), протекающий по резистивному элементу R под действием приложенного напряжения u(t), то мгновенная мощность, развиваемая при этом будет равна Понятие энергетического спектра оказывается весьма полезным для получения различных инженерных оценок, устанавливающих реальную ширину спектра сигналов очень сложной формы. Явление появления погрешностей (затухающих колебательных процессов) в окрестностях точек разрыва восстановленного импульса, возникающее при усечении линейчатого спектра(ограничении числа используемых гармоник), получило название явления Гиббса. Проблемы спектрального анализа и синтеза сигналов, быстроизменяющихся и ограниченных по времени, частично решаются переходом к так называемому кратковременному или оконному преобразованию Фурье. Кратковременное преобразование выполняется с использованием выражения: Здесь, в отличие интеграла Фурье, функция u(t) под знаком интеграла дополнительно умножается на оконную функцию w(t — b). Параметр b окна задает его сдвиг на временной оси.

43. Поясните необходимость, назначение и суть вейвлет - преобразований сигналов. На основании понятия о векторном пространстве мы представили сигнал в виде обобщенного ряда Фурье (4.1), т. е. как взвешенную сумму простых составляющих — базисных функций помноженных на коэффициенты С_к. «Геометрически» ряд Фурье означал разложение произвольного сигнала, как некого вектора, при котором коэффициенты ряда Фурье есть проекции на базисные направления. Мы установили, что коэффициенты разложения в ряд Фурье дают достаточно ясную качественную характеристику сигналу. Они показывают насколько u(t) содержит в себе эталонные колебания . 1. Имеют вид коротких, локализованных по времени волновых пакетов с нулевым значением интеграла, определяющего площадь под кривой, описывающей сигнал. 2. Обладают возможностью сдвига по времени. 3. Способны к масштабированию. 4. Имеют ограниченный частотный спектр. В основе вейвлет - преобразования лежит использование непрерывных и интегрируемых по всей оси времени t двух классов функций. 1. Масштабирующей или скейлинг - PHI функции , определяющей грубое приближение сигнала и порождающей аппроксимирующие коэффициенты.

Масштабирующая функция должна удовлетворять определенному уравнению, называемому масштабирующим. Кроме того, должно выполняться Масштабирующая функция порождает вейвлет функцию Хотя, следует иметь в виду, что масштабирующие PHI функции присущи только ортогональным вейвлетам. Для иных они могут не существовать. 2. Вейвлет – функций PSI с нулевым значением интеграла определяющих детали сигнала и порождающих детализирующие коэффициенты. Система вейвлет –PSI функций создается на основе той или иной базисной функции . Базисная функция , помимо отмеченных требований, должна обеспечивать выполнение двух основных операций: смещение по оси времени t - ; масштабирование .

44. Прямое и обратное вейвлет - преобразования. Особенность диадного вейвлет - преобразования. Кратко опишите схему вейвлет - анализа сигнала. Определите суть и назначение аппроксимирующих и детализирующих коэффициентов разложения.

Вейвлет (wavelet) – это обобщенное название временных функций, имеющих вид волновых пакетов той или иной формы, локализованных по оси независимой переменной (по оси времени t) и способных к сдвигу по ней и масштабированию (сжатию или растяжению).

Прямое вейвлет-преобразование, в соответствии с общепринятым подходом к анализу сигналов, означает разложение произвольного сигнала по принципиально новому базису в виде, что очень значимо, совокупности волнообразных пакетов-вейвлетов, которые характеризуются четырьмя принципиально важными свойствами:

1. Имеют вид коротких, локализованных по времени волновых пакетов с нулевым значением интеграла, определяющего площадь под кривой, описывающей сигнал.

2. Обладают возможностью сдвига по времени.

3. Способны к масштабированию (сжатию или растяжению вдоль оси времени).

4. Имеют ограниченный (или, точнее, локальный) частотный спектр.

Наряду с прямым вейвлет – преобразованием, осуществляющим анализ сигнала, существует обратное вейвлет-преобразование, с помощью которого можно осуществлять синтез сигналов.

Обратное непрерывное вейвлет-преобразование обычно записывают следующим образом

где К_ψ – константа(нормирующий коэффициент), зависящий от ψ,

- Фурье-преобразование вейвлета ψ(t).

По формальной аналогии с преобразованием Фурье, путем вычисления вейвлет коэффициентов, можно получить непрерывное прямое вейвлет-преобразование (CWT – continuous wavelet transform)

При непрерывном изменении а и b для расчета вейвлет спектра необходимы большие вычислительные затраты. Поэтому для практического применения необходима дискретизация значений а и b. Дискретизация как правило осуществляется через степени двойки

где m и k – это целые числа. В этом случае плоскость аb превращается в соответствующую сетку. Сетка дискретизации называется диадической. Соответственно такое преобразование принято называть диадным (dyadic) вейвлет- преобразованием.

Важной особенностью диадного вейвлет-преобразования является исключение перекрытия носителей вейвлетов, т. е. устранение избыточности в ходе вейвлет-преобразований.

Одна из основополагающих идей вейвлет-представления сигналов заключается в том, что аппроксимация в пространстве сигналов достигается суммированием составляющих так называемого грубого приближения и составляющих, отражающих различные уточнения при приближении. Поэтому сразу же следует отметить, что коэффициенты разложения, получаемые при прямом вейвлет-преобразовании, по своей сути, принципиально отличаются от коэффициентов преобразования Фурье для гармонических функций. Набор коэффициентов, получаемый в ходе прямого вейвлет преобразования и содержащий информацию о конкретном сигнале, состоит из «грубых», аппроксимирующих и «уточненных», детализирующих. Это позволяет по иному, нежели раньше, обрабатывать их.