§3.2 Исследование Multi-VaR-схемы

Сравнение алгоритмов решения оптимизационной задачи. Для исследования MultiVaR в качестве схемы для поиска эффективных портфелей сравним используемые для нахождения решения алгоритмы численного расчета. Сравнение вычислительных затрат (вычислительной эффективности) двух алгоритмов численного решения задачи формирования эффективных портфелей в рамках MultiVaR-схемы привело к следующим результатам: Алгоритм 1 в среднем сходится за количество итераций в 2.5 раза меньшее, чем Алгоритм 2 (алгоритм с весами). Кроме того, при некоторых условиях Алгоритм 2 в окрестности максимума, в том числе и локального, может иметь проблемы со сходимостью: итерационные приближения решения начинают «колебаться» (не являются монотонно убывающими). В этом случае необходимо использовать ограничение на количество итераций.

Сравнение, таким образом, приводит к выводу, что Алгоритм 1 является более эффективным с точки зрения вычислительных затрат. Необходимым условием применения именно этого алгоритма численного расчета в качестве основного является идентичность результатов, полученных обоими алгоритмами. Примеры решений и выводы, связанные с идентичностью, представлены ниже.

В дальнейшем, если не оговорено противное, рассматривается решение задачи при следующем наборе параметров: и равномерном распределении множества вероятностей на интервале [0;1].

Ниже используется термин «квантиль» (или «процентиль») – такое число, которое с заданной вероятностью превышают значения рассматриваемой случайной величины.

Сравнение полученных результатов при различном числе взятых для оптимизации точек (квантилей). В поставленной задаче имеем фиксированное множество вероятностей и соответствующее ему множество квантилий , которое подлежит оптимизации.

В результате исследования было выяснено, что для равномерного распределения вероятностей на отрезке [0;1] или на любых других отрезках внутри данного решение оптимизационной задачи слабо зависит от количества критериев-квантилий, т.е. от величины m. Разница между получаемыми эффективными портфелями менее 5%. Зависимость от выбранного отрезка, на котором распределены значения вероятностей, проявляется более четко. Соответствующие результаты приведены в Таблице 3.1.

Для анализа результатов в дальнейшем используется функция зависимости эффективности решения задачи в выбранном смысле от левой и правой границы отрезка (соответственно ), на котором равномерно распределены числовые значения параметров : .

На плоскости при некоторых наборах входящих данных имеются узкие области, в которых функция имеет небольшие пики. В результате при уменьшении числа границы областей становятся более «размытыми» и пики сглаживаются.

Таблица 3.1. Таблица зависимости результата оптимизации от отрезка.

Отрезок.	[0;1]	[0,25;0,75]	[0,3;0,7]	[0,35;0,65]	[0,43;0,57]
Значение эффективности	0,000174732	0,000173941	0,000176941	0,000174732	0,000177109
x[0]	0	0,0277778	0	0	0
x[1]	0	0	0	0	0
x[2]	1	0,972222	0,940329	1	0,950231
x[3]	0	0	0	0	0
x[4]	0	0	0	0	0
x[5]	0	0	0,0596708	0	0
x[6]	0	0	0	0	0,0335648
x[7]	0	0	0	0	0
x[8]	0	0	0	0	0,0162037
x[9]	0	0	0	0	0

Отметим, что вышеперечисленные свойства имеют место для обоих алгоритмов численного расчета, а полученные результаты имеют разницу менее чем в 1%.

VaR-схема как частный случай Multi-VaR-схемы.

Как уже отмечалось выше, VaR-схема имеет вид:

, (3.2)

где X – множество ограничений на x, - вероятность выполнения неравенства (т.е. вероятность того, что значение эффективности портфеля примет значение меньше некоторого уровня ).

Таким образом, мы видим, что VaR-схема является частным случаем Multi-VaR-схемы при . Решение задачи по схеме VaR может быть получено с помощью разработанной схемы, приравниваем или же путем обнуления всех коэффициентов компромисса кроме одного, для которого , т.е. . Итак, видно, что можно прийти к VaR-схеме путем изменения весовых множителей.

Решение задачи по схеме VaR дает решение, которое нельзя однозначно сравнить с полученным в Multi-VaR-схеме, ввиду множества возможных значений параметров. Решение данной проблемы будет рассмотрено в дальнейшем.

Исследование VaR-схемы как частного случая Multi-VaR-схемы. Для VaR постановки характерно для двух алгоритмов численного расчета поведение, представленное на Рис.3.1:

p

ef

Рис.3.1 График зависимости эффективности портфеля от значения параметра VaR-схемы задачи оптимизации: ef(p).

Исследование чувствительности (зависимости) результата формирования эффективных портфелей от входных величин (параметров) Multi-VaR-схемы (от их количества и числовых значений).

А) Зависимость от количества входных данных: исследование проведено для обоих алгоритмов, полученные результаты различаются менее чем на 1%; общий вид решения, а именно вид поверхности (Приложения 1), не изменился; получаемые эффективные портфели претерпели изменения ввиду вовлечения в рассмотрение новых данных.

Б) Зависимость от числовых значений входных данных: исследование проведено для обоих алгоритмов, полученные результаты различаются менее чем на 1%; общий вид решения, а именно вид поверхности , для различного набора источников входных данных изменяется; конкретно получаемые эффективные портфели претерпевают изменения, что является ожидаемым результатом.

В ряде проведенных сравнений и исследований была показана идентичность результатов, полученных с помощью алгоритмов численного расчета. Убедившись в этом и учтя оговорки, сделанные в начале этого параграфа, в дальнейшем при исследовании свойств Multi-VaR-схемы для экономии времени будем использовать Алгоритм 1.

Сравнение Multi-VaR-схемы со схемой Марковица и VaR-схемой

Для схемы Марковица характерным является поведение на критериальной плоскости , представленное на Рис.3.2.

m_p

σ_p

Рис.3.2 Решение оптимизационной задачи по схеме Марковица на критериальной плоскости .

Поскольку для оценки эффективности полученного при решении портфеля мы избрали несколько другой критерий, то проследим его зависимость его от (Рис.3.3) в рамках решения задачи по схеме Марковица.

m_p

ef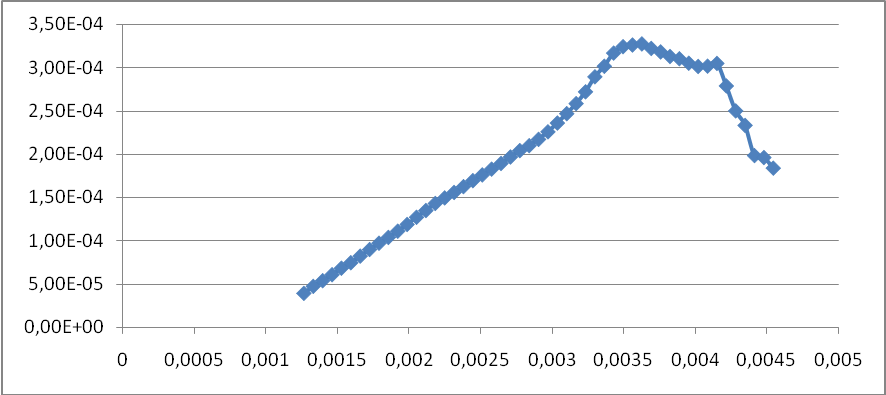

Рис.3.3 Зависимость для решений задач,

полученных по схеме Марковица.

Сравнение полученного решения по схеме Маковица с решением задач по VaR-схеме и Multi-VaR-схеме с помощью эффективности в вышеуказанном смысле представляет некоторые сложности, ввиду различности критериев и невозможности однозначного перехода от одних критериев к другим.

Однако в данной постановке задачи имеется возможность сравнения с помощью рассмотрения динамики поведения сформированного портфеля (аналогичным способом, можно сравнить VaR-схему и Multi-VaR-схему).

Рассмотрим выборки эффективностей с положительной в целом динамикой и разделим их по «времени» на две части. По первой части выборки сформируем эффективные портфели: , соответственно, по схеме Марковица, VaR-схеме, Multi-VaR-схеме. Введем также в рассмотрение равномерно распределенный портфель . На второй части выборки проследим поведение портфеля и эффективных портфелей и оценим их эффективность на основе коэффициента наклона γ прямой, являющейся ближайшей в среднеквадратичном смысле к динамическому процессу (Приложения 2).

Таблица.3.2 Значения коэффициента γ.

	Значения коэффициента γ, 10-2
γ(	1.245
γ(	1.458
γ(	1.421
γ(	1.602

Значение коэффициента для эффективного портфеля по Multi-VaR-схеме является максимальным среди остальных и получено путем подбора значений параметров схемы.

Помимо рассмотренной оценки, которая характеризует лишь значение эффективности портфеля, можно ввести такие критерии как среднеквадратичный разброс и «просадка» портфеля – характеристики, имеющие смысл риска. Серия численных экспериментов показала, что и в этом случае решение задачи по Multi-VaR-схеме и соответствующий подбор параметров позволяет оптимальным образом сформировать эффективный портфель.

Multi-VaR-схема является гибкой схемой, в силу большого количества параметров, и представляет возможности получения решения с заданными характеристиками или максимально приближенного к нему.