Лекция 6. Средние величины

Среди показателей, характеризующих статистические совокупности, важное место занимают средние величины.

Средняя величина – показатель, который даёт обобщённую (усреднённую) характеристику единиц изучаемой совокупности. В средней величине отражается то общее, что имеется в каждой единице совокупности.

Сущность статистической обработки методом средней величины заключается в замене индивидуальных значений признака их средним показателем. При этом общий объём совокупности остаётся неизменным.

Пример: есть данные о выработке 5 рабочих: 135, 141, 153, 159, 162. Определить среднюю выработку. .

Средние величины, которые необходимо знать наизусть:

- средняя арифметическая;

- средняя гармоническая;

- средняя хронологическая;

- средняя квадратическая, кубическая;

- средняя геометрическая;

- структурные средние: мода, медиана.

1. Средняя арифметическая: чаще всего в статистике и социально-экономических исследованиях применяется арифметическая величина.

Средняя арифметическая простая рассматривается в случаях, когда значение признака повторяется один или одинаковое число раз в ряде распределения:

, где n-количество единиц совокупности.

Средняя арифметическая взвешенная применяется в случаях, когда каждое значение признака повторяется неодинаковое число раз, или частота ряда распределения превышает единицу хотя бы для одного признака:

, где f-вес.(сколько раз повторяется каждая еденица совокупности)

2. Средняя гармоническая: в ряде случаев бывают известны варианты (x) и произведения варианты на частоту (x∙f), в то время как сами частоты (f) неизвестны, тогда применяется средняя гармоническая, которая бывает простой и взвешенной. .

Произведение x∙f выражается через сложный экономический показатель M (M= x∙f). Для расчёта средней величины, когда x∙f =M=1, применяется средняя гармоническая простая: . Если x∙f =M≠ 1, то для расчёта применяется средняя гармоническая взвешенная: .

Средняя гармоническая – величина, обратная средней арифметической, из обратных значений признака.

Свойства средних величин

1. Если от каждой варианты отнять или прибавить одно и то же число, то средняя увеличится или уменьшится на то же число.

2. Если каждую варианту увеличить или уменьшить в a раз, то средняя увеличится или уменьшится в столько же раз.

3. Если все частоты увеличить или уменьшить в a раз, то средняя не изменится.

4. Если все частоты увеличить или уменьшить на a, то средняя изменится непредсказуемо.

5. Средняя арифметическая суммы нескольких величин равна суме средних арифметических этих величин.

6. Алгебраическая сумма отклонений значений признака от средней арифметической всегда равна нулю.

Пример: Найти среднюю урожайность в 2003 и 2004 гг.

№ колхоза	2003 г.		2004 г.
	урожайность (ц/га)	площадь (га)	урожайность (ц/га)	Валовой сбор(ц)
1 2 3	40 50 60	1000 2000 3000	38 49 65	40000 100000 150000

Решение:

, где f-вес

(ц/га)

.

(ц/га)

3. Средняя хронологическая: применяется для расчёта средней величины, если исходные данные представлены на определённые даты, моменты времени:

Пример: Найти среднюю стоимость ОПФ

дата	1.01	1.02	1.03	1.04	1.05	1.06
стоимость ОПФ	100	120	110	120	140	140

Решение:

, , ,

, .

Приведем все расчеты к одному знаменателю: Х=‎‎‎

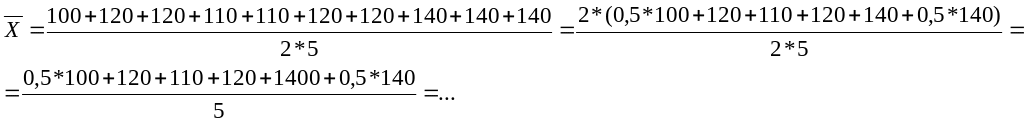
4. Средняя квадратическая: применяется для измерения вариации признака в совокупности:

,

5. Средняя кубическая: .

6. Средняя геометрическая: применяется чаще всего для определения средних темпов роста в единицу времени: , ,

Пример: Рассчитайте среднегодовые темпы роста

показатели	год
	1995	1996	1997	1998	1999
выпуск продукции	20	22	26	50,1	100,2
	х1	х2	х3	х4	х5
коэффициент роста выпуска продукции	−	1,1	1,2	1,9	2
		k1	k2	k3	k4

Решение:

, где m=n-1.

.

Средняя геометрическая, чаще всего, применяется в экономических расчетах, но учитывает только начало и конец ряда и недостаточно точно отражает динамику изменения, т.е. она не учитывает сумму ряда.

7. Средняя кумулятивная: .

Формула кумулятивной средней более чётко отражает динамику изменений и помогает увидеть сумму ранжированного ряда.

Все рассмотренные средние величины (кроме средней хронологической) являются степенными средними и выводятся из следующей формулы: , где получается при

k=-1 − средняя гармоническая;

k=0 − средняя геометрическая;

k=1 − средняя арифметическая;

k=2 − средняя квадратическая;

k=3 − средняя кубическая.

Все эти показатели рассчитываются для варьирующего признака для простых средних. Если все значения признака в ряде распределения одинаковы, то все значения средних равны. Между указанными средними величинами имеет место зависимость (для одного ряда распределения):

− это неравенство называется правилом мажорантности средних величин.

8. Структурные средние:

1) Структурное среднее мода (Mо) – наиболее часто встречающееся значение ряда, другими словами, мода – это варианта, имеющая наибольшую частоту. В дискретных рядах мода определяется визуально, в интервальных рядах визуально определяется модальный интервал, а мода (точечная) определяется по формуле: , где

x₀ − нижняя граница модального интервала;

i − шаг интервального ряда;

f_Mо − частота модального интервала;

f_Mо-1 − частота интервала, предшествующего модальному;

f_Mо+1 − частота интервала, следующего за модальным.

Пример: Найти Мо в дискретном и интервальном рядах.

дискретный ряд:	разряд	1	2	3	4	5	6
	кол-во рабочих	10	20	100	30	70	50

интервальный ряд:	% выполнения плана	До 100	100-140	140-180	свыше 180
	кол-во рабочих	20	80	150	50

.

2) Структурное среднее медиана (Mе) – значение, которое делит ранжированный ряд пополам.

В нечётных, чётных и дискретных рядах медиана определяется визуально, но в дискретных рядах она определяется с помощью накопленных частот. В интервальном ряду медианный интервал находится визуально, с помощью накопленных частот, а сама медиана (точечно) по формуле: , где

x₀ − нижняя граница медианного интервала;

i −шаг интервального ряда;

∑f − сумма накопленных частот;

S_Me-1 − сумма частот, накопленных до медианного интервала;

f_Me − частота медианного интервала.

Пример: Найти Ме в нечетных, четных, дискретных, интервальных рядах.

нечётный ряд: чётный ряд:

число детей в семье

0

1

2

3

4 и более

число детей в семье

0

1

2

3

4

5 и более

дискретный ряд:

разряд	1	2	3	4	5	6	∑
кол-во рабочих	10	20	60	70	30	10	200

интервальный ряд:

% выполнения плана	до 100	100-120	120-140	140-160	160-180	св.180	∑
кол-во рабочих	20	50	70	120	140	100	500

.

Если х сред. равно Мо = Ме – это симметричное распределение, если х сред не равно Мо, не равно Ме – распределение ассиметричное.