38. Корреляция: цели, виды.

К орреляция - мера зависимости переменных =сила взаимосвязи в данных.

Линейная связь между 2-мя переменными –ПАРНАЯ ЛИНЕЙНАЯ КОРРЕЛЯЦИЯ

Интерпретация коэффициента корреляции Пирсона: отклонение признака-фактора от его среднего на величину стандартного отклонения в среднем приводит к отклонению признака-результата от своего среднего на величину r его стандартного отклонения.

Корреляция бывает линейной, нелинейной и ложной.

Коэффициент корреляции Пирсона

0,7 ≤ | Rxy | ≤ 1 Сильная корреляция

0,5 ≤ | Rxy | ≤ 0,7 Средняя корреляция

0,3 ≤ | Rxy | ≤ 0,5 Слабая корреляция

0 ≤ | Rxy | ≤ 0,3 Незначимая корреляция

• Применение коэффициента корреляции: Если связь линейная!

Меры тесноты парной связи

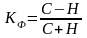
Коэффициент Фехнера

Коэфициент Спирмена

где di – разность рангов по обоим признакам

для каждого объекта

Множественная корреляция

39. Надежность коэффициента корреляции.

Н адежность коэффициента корреляции

то есть коэффициент корреляции находится в пределах r±3σ.

40. Регрессия: цели, виды

Регрессия – одностороння вероятностная зависимость между случайными величинами. Регрессия устанавливает соответвие между этими величинами. Регрессией так же является функция, при помощи которой выражается односторонняя стохастическая зависимость.

Регрессия бывает линейной и нелинейной.

Целью регрессионного анализа является предсказание значения одного фактора на основе значения другого.

В ходе регрессионного анализа решаются две основные задачи:

• Построение уравнения регрессии, т.е. нахождение вида зависимости между результатным показателем и независимыми факторами x1, x2, ..., xn.

• Оценка значимости полученного уравнения, т.е. определение того, насколько выбранные факторные признаки объясняют вариацию признака у.

Линейная регрессия

Уравнение парной регрессии:

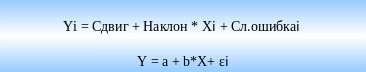
Параметры уравнения парной линейной регрессии вычисляются

с помощью МЕТОДА НАИМЕНЬШИХ КВАДРАТОВ

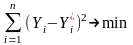
т.е. сумма квадратов отклонений эмпирических значений

зависимой переменной от вычисленных по уравнению регрессии

должна быть минимальной.

Вид кривой неизвестен:

Оценка кривой:

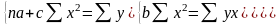• Параболическая связь -

• Экспоненциальная связь -

• Гиперболическая связь -

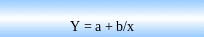
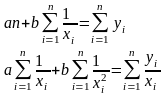
Коэффициент детерминации

У казывает, какая доля вариации результативного признака объясняется влиянием всех X – переменных.

41. Регрессия: ошибка выбранной математической модели.

y – эмпирическое значение

y* - теоретическое значение

p – число параметров уравнения

42. Множественная регрессия.

Множественная регрессия

Регрессионные коэффициенты (или B-коэффициенты) представляют независимые вклады каждой независимой переменной в предсказание зависимой переменной.